Różniczkowania odcinek trzeci. Tym razem na prostej. Do tej pory próbowałem przekonywać o istotnej roli układu współrzędnych przy wyliczaniu pochodnych cząstkowych. A jak to jest, gdy dziedzina funkcji jest jednowymiarowa?
Funkcja x czyli identyczność
Przypadek jednowymiarowy jest na tyle zdegenerowany, że wiele aspektów, szczególnie poruszanych w poprzednich dwóch notkach w ogóle w nim nie występuje. Wielu z nas pamięta ze szkoły, że pochodna funkcji f jest oznaczana primem: f'. Dlaczego prawie nigdy nie trzeba było dopowiadać „po czym” się różniczkuje? Otóż dlatego, że na prostej R istnieje pewna wyróżniona funkcja – identyczność. Zwykle oznacza się ją literką x.
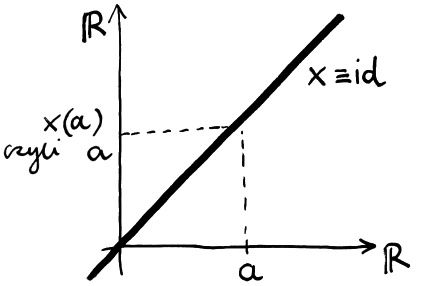
x: R ∋ a ↦ x(a) ≡ a ∈ R
No tak: to najprostsza funkcja liniowa o współczynniku kierunkowym równym 1 i wyrazie wolnym równym 0. Przy tej okazji, wypada wspomnieć o pewnym wstydliwym problemie dotyczącym zapisu. Ponieważ literką x nazywa się również elementy prostej R czyli po prostu liczby, można mieć wątpliwości co do znaczenia użytych liter. Zobaczmy na przykład wyrażenie:
cos(2x)
Może ono oznaczać liczbę – wartość funkcji cosinus w punkcie 2x (x też jest wtedy liczbą). Ale jeśli już ktoś będzie chciał policzyć pochodną z tego wyrażenia, no to wtedy 2x będzie funkcją wewnętrzną, a nawiasy nie będą oznaczać pobierania argumentu, tylko złożenie funkcji.
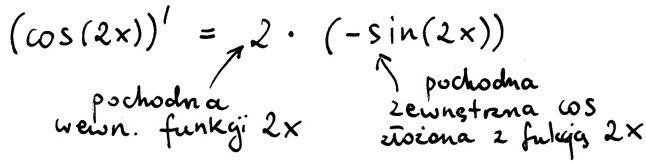
OK, nie od dziś wiadomo, że zarówno w fizyce jak i matematyce stosuje się te same symbole na różne wielkości. Czasami – ale rzadko – prowadzi to zabawnych nieporozumień. Tak już jest i chyba nic tego nie zmieni. Ja w każdym razie nie pozwoliłem sobie na zbyt częste odchodzenie od tej trwale zakorzenionej tradycji.
Zostawmy jednak tę dygresję i przejdźmy do tematu głównego.
Dlaczego prim (nie) wystarcza?
Skoro na prostej jest wyróżniona funkcja x, to prawie zawsze będziemy różniczkować po niej. Czyli badać zmienność funkcji w zależności od zmian x. Czyli prawie zawsze nie musimy zaznaczać tego x w wyrażeniu:
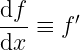
ograniczając się do prima.
Ale skoro tak właśnie napisałem, to pewnie zaraz podam wyjątek od powyższego „prawie zawsze”. Właśnie, takich przykładów trochę jest i nazywają się one całkowaniem przez podstawienie, bardziej swojsko znane jako wykorzystanie pomocniczej zmiennej.
Żeby długo nie szukać, wziąłem pierwszy przykład umieszczony w polskiej Wikipedii. Chodzi o rozwiązanie równania różniczkowego:
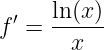
Przepiszę to równanie nieco inaczej. Po pierwsze – ponieważ będę różniczkował nie tylko po x, napiszę jawnie po czym różniczkowana jest f. Po drugie – ponieważ x oznacza identyczność, to złożenie jej z logarytmem daje po prostu logarytm.
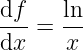
Do rozwiązania tego równania skorzystam z twierdzenia, jak przeliczyć sobie pochodne przy zmianie układu współrzędnych[1]:
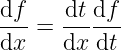
Wzór obowiązuje dla wszystkich, wystarczająco dobrych funkcji t, więc pewnie dla ln też.
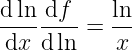
Ponieważ (d ln/dx) = 1/x, można to równanie zapisać:
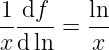
Skracamy, mnożąc przez x:
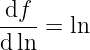
I znajdujemy bez kłopotu funkcję f:
f = (1/2) ln2 + stała
Zwykle, żeby nie drażnić mózgu niepokojącym zapisem, oznaczającym, że możemy różniczkować po funkcji logarytmu, wprowadza się symbol, który powinien być mentalnie wystarczająco bliski x, by mózg nie poczuł się podrażniony. Na przykład w Wikipedii wprowadzają „pomocniczą zmienną” t=ln. Ale to głównie po to, żeby nie burzyć sobie przyzwyczajenia, że „różniczkujemy po zmiennej”. Bo być może naszym mózgom łatwiej jest rozwiązać takie równanie:
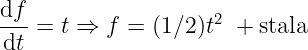
* * *
Ponieważ staram się „uczyć, bawiąc” to na koniec wynurzeń o różniczkowaniach, które w zamierzeniu miały stanowić zabawę, zamieszczę mały element uczący. Otóż często spotykany symbol:
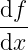
bynajmniej nie stanowi sobą dzielenia df przez dx. Bo niezależnie od wysoce użytecznych intuicji, nie da się w obszarze standardowej analizy zdefiniować czegoś, co nadawało by się do dzielenia i co można by nazwać różniczką funkcji. A przynajmniej ja nic o tym nie wiem. Więc co to w takim razie jest? Po prostu zapis oznaczający pochodną.
Można też sobie pomyśleć – i to chyba najlepsze podejście – że chodzi o działanie operatora (d/dx) na funkcję f, gdzie wynikiem działania jest pochodna funkcji.
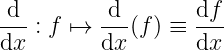
Mając uspokojone sumienie, że „uczyłem” a nie tylko „bawiłem”, zakończę na razie temat liczenia pochodnych.
[1] Wersja wielowymiarowa tego twierdzenia wygląda następująco:
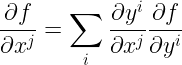
Piszę o tym, żeby ktoś nie pomyślał, że w jednym wymiarze obowiązuje „dzielenie różniczek” i że można sobie je tak po prostu „skrócić”, albo „pomnożyć i podzielić przez różniczkę”. Zauważmy też, że indeks j przy zmiennej xj, wyraźnie sugeruje, że zostały wybrane wszystkie funkcje { xj } tworzące układ współrzędnych, co jak wiadomo z poprzednich notek jest konieczne, by w ogóle mówić o pochodnej cząstkowej.
Inne tematy w dziale Technologie

