Nie będę udawać, że poniższy tekst jest dziełem mojego samodzielnego studiowania tajemnic analizy matematycznej. Jest on raczej próbą wgryzienia się w jeden z wykładów prof. Zbigniewa Oziewicza – legendy wrocławskiej fizyki teoretycznej. Jego kurs analizy miał miejsce w roku 1986/7 i pożytecznym jest czasami coś sobie z tej przygody przypomnieć.
* * *
Przyzwyczajenia nabyte przy liczeniu pochodnych funkcji o jednowymiarowej dziedzinie powodują, że w większej liczbie wymiarów wiele rzeczy może budzić wątpliwości.
Jak to jest w jednym wymiarze
Zobaczmy jak liczy się pochodną, kiedy dziedzina jest prostą albo jej kawałkiem. Przede wszystkim liczymy pochodną w którymś punkcie. Upraszczając sprawę: Jak da się ją policzyć dla każdego punktu dziedziny funkcji, to w ten sposób dostaniemy inną funkcję, zwaną pochodną funkcji. Ale zaczynamy od pojedynczego punktu.
No to mamy jakiś punkt x0 i wartość funkcji w tym punkcie f(x0). To dwie liczby. Żeby policzyć trzecią liczbę – pochodną:
- wybieramy jakiś inny punkt dziedziny, ale bliski x0, czyli x0+h (h jest nieduże);
- potem patrzymy jaka jest wartość funkcji niedaleko naszego x0, czyli f(x0+h);
- liczymy o ile wzrosła/zmalała funkcja na odcinku między x0 a x0+h, czyli f(x0+h)–f(x0);
- liczymy tzw. wyrażenie różnicowe: (f(x0+h)–f(x0))/(x0+h–x0), czyli (1/h)∙(f(x0+h)–f(x0));
- liczymy granicę powyższego wyrażenia różnicowego dla h → 0 i oznaczamy ją f’(x0) albo (df/dx)(x0)
Może jaśniej będzie to widać na obrazku:
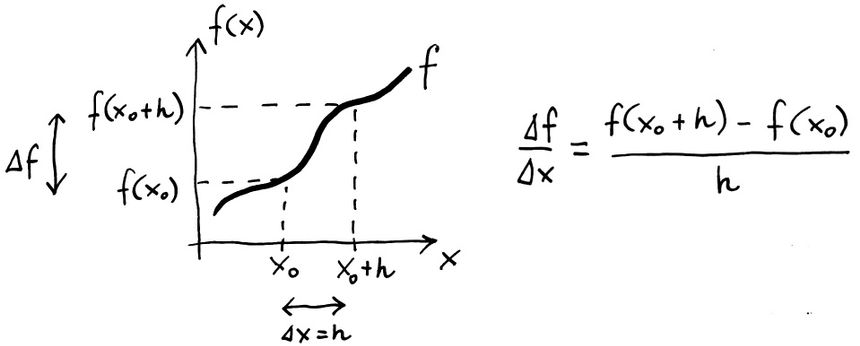
Spróbujmy powtórzyć powyższą procedurę dla jakiegoś punktu A i jakiejś funkcji f np. na płaszczyźnie. W pierwszym kroku musimy wybrać jakiś inny, bliski A punkt. Oznaczymy go jako A'. Ale który wybrać?
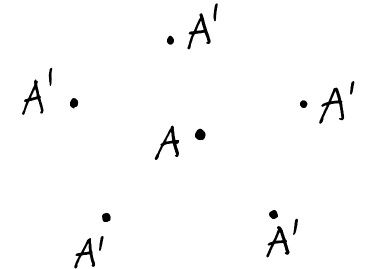
O czego to zależy? Dalej zobaczymy, co będzie potrzebne, żeby policzyć:
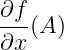
przy założeniu, że x i f są wystarczająco dobrymi funkcjami. Ale najpierw trochę opowiem o funkcjach.
Poziomice
Zastanówmy się, jak zobrazować funkcję na płaszczyźnie. Istnieje na to kilka sposobów. Jednego z nich uczymy się na geografii. Zobaczmy jak wygląda obrazek pokazujący funkcję „wysokość”:
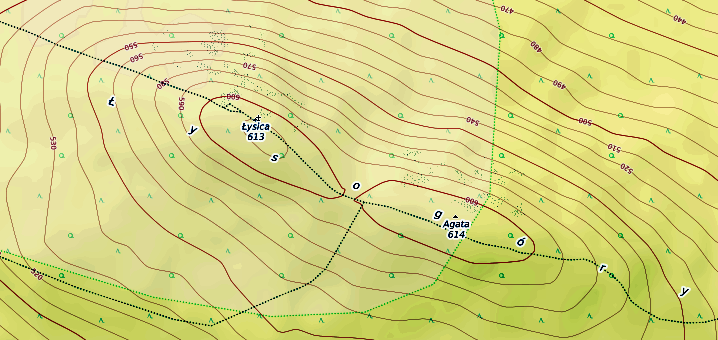
Jest ona przedstawiana za pomocą poziomic. Poziomica to linia zbudowana z punktów dla których funkcja przybiera te same wartości. W czasie prognoz pogody możemy czasami zobaczyć poziomice funkcji „ciśnienie” i „temperatura”, ale wtedy nazywają się one „izobara” i „izoterma”.
Dla funkcji określonej na zwykłej, trójwymiarowej przestrzeni poziomicą będzie dwuwymiarowy zbiór, dla funkcji na płaszczyźnie – krzywa. Ogólnie dla n-wymiarowej przestrzeni, poziomicą będzie (n-1)wymiarowy zbiór, jeśli używamy – przypominam – wystarczająco ładnych funkcji.
Żeby oswoić się z pojęciem poziomicy, poniżej obrazkowo kilka (koślawych) rysunków, poziomic różnych funkcji na płaszczyźnie:

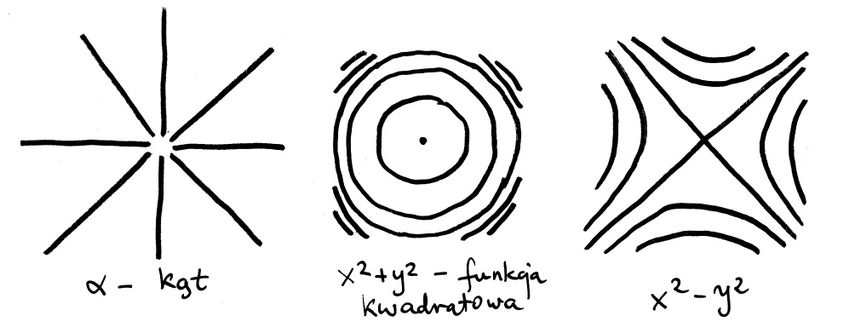
Powyższe przykłady dotyczą sytuacji, kiedy {x, y} jest kartezjańskim układem współrzędnych. Ale na razie zapomnijmy, że możemy mieć jakieś intuicje rodem ze znanego ze szkoły układu, z osiami X, Y czy Z. Chcę pokazać, jak matematycznie definiowana jest pochodna w dowolnym układzie współrzędnych. Zauważmy, że w poprzedniej notce, dla dwuwymiarowego zbioru będącego modelem gazu doskonałego wręcz nie da się wprowadzić układu kartezjańskiego. Choćby z powodu jednostek.
Od tej pory wymagam od funkcji x i y tylko tyle, by były na dość ładne, żeby mogły tworzyć układ współrzędnych na płaszczyźnie. Nie musi być to układ kartezjański ani nawet krzywoliniowy ortogonalny[1].
(w końcu) liczymy pochodną
No to zabieramy się do liczenia pochodnej cząstkowej względem funkcji x. W książkach mówi się „pochodna cząstkowa względem zmiennej x”, ale my już wiemy, że w zagadnieniu liczenia pochodnych „zmienna” to inaczej „funkcja”. Czasami – jak się okaże nie do końca poprawnie – mówi się „pochodna cząstkowa w kierunku x”. Tylko czy funkcja x w ogóle wyznacza jakiś kierunek?
Wróćmy do przykładu. Na jednej z poziomic funkcji x mamy nasz punkt A. Wybieramy punkt A' na niedaleko położonej poziomicy. Powtórzę zadane wcześniej pytanie: Ale który wybrać?
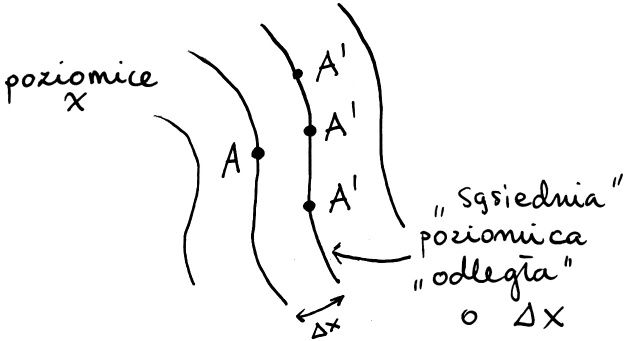
Spostrzegawczy czytelnik zauważy, że w przypadku jednowymiarowym nie było kłopotu z wyborem, bo poziomice x były punktami.
I tu w potrzebie przychodzi nam z pomocą druga funkcja – nazwę ją y – która, co prawda na pierwszy rzut oka nie wydaje się potrzebna, ale jest kluczowa przy określaniu „kierunku”. Uzupełnię powyższy obrazek o poziomice funkcji y. Teraz chyba widać, jaki punkt trzeba wybrać?
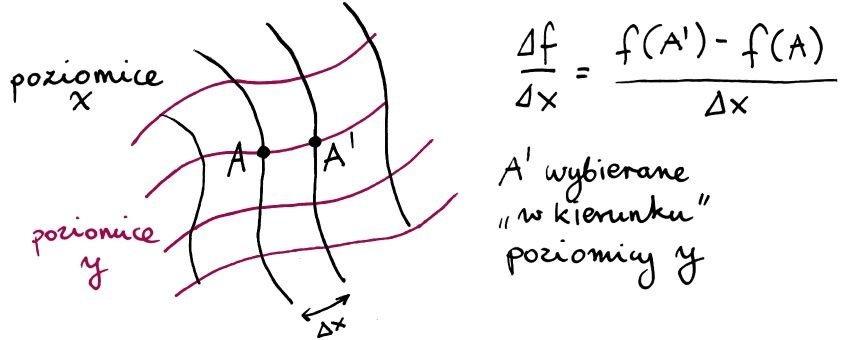
No właśnie. Paradoksalnie to, co w podręcznikach jest opisywane jako „pochodna cząstkowa względem x”, jest wyznaczone przez poziomice reszty funkcji wybranego układu współrzędnych. Czyli, wracając do pochodnych na płaszczyźnie, stosowany symbol (∂/∂x) jest określony przede wszystkim przez funkcję y. Przy „pierwszym czytaniu” może się to wydać trochę dziwne, ale tak jest.
Teraz już chyba wiadomo, dlaczego przy wyborze innego układu {x, s} symbol (∂/∂x) będzie oznaczał coś innego niż w poprzednim {x, y}.
Jeśli chwilę się zastanowisz, to zauważysz, że wybieranie punktów do liczenia wyrażenia różnicowego na poziomicach funkcji „towarzyszących”, jest równoznaczne z potocznym określeniem pochodnej cząstkowej: „pozostałe zmienne traktujemy jako stałe parametry”.
[1] Zgodnie z uwagą Bjaba z poprzedniej notki: ortogonalność nie jest w ogóle potrzebna do definiowania pochodnych cząstkowych. Niestety mając ją i tylko jedną funkcję x, można jednoznacznie określić pochodną (∂/∂x), bez udziału pozostałych funkcji układu współrzędnych.
Inne tematy w dziale Technologie

