Pewnie wiecie co to liczby pierwsze. Jeśli tak, to spójrzcie na spiralę Ulama.

Robi się ją tak, że spiralnie wypisuje się kolejne liczby naturalne, zaznaczając liczby pierwsze.
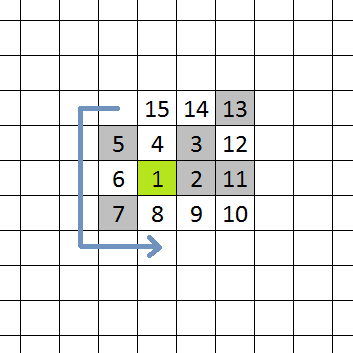
Wypisane na płaszczyźnie liczby pierwsze – 2, 3, 5, 7, 11, 13, 17… – tworzą dość regularne wzory, pomimo, że ciężko doszukać się regularności gdy wypiszemy je tak po prostu na osi liczbowej. Na taki pomysł wpadł nasz rodak Stanisław Ulam w 1963. Wcześniej wpadał na inne bardzo dobre pomysły (np. metoda Monte Carlo), choć niektóre z nich nie były fajne (był współautorem koncepcji bomby wodorowej).
Aż dziwne, że takie regularne obrazki powstały dopiero w XX wieku, skoro tak łatwo je wygenerować, a przecież tym zagadnieniem zajmowało się wcześniej wiele osób. Ale zostawmy dziwności i spróbujmy poprawić obrazek. Białe pola z pierwszego rysunku oznaczają liczby złożone. Pomyślałem sobie, że może warto sprawdzić stopień ich złożoności i przemalowałem obrazek. Teraz białe pola odpowiadają liczbom pierwszym, różowe iloczynom dwóch liczb pierwszych (np. 4=2×2, 6=2×3…), jasnobrązowe to iloczyny trzech liczb (8=2×2×2, 12=2×2×3…) itd. Im ciemniejszy punkt, tym bardziej liczba jest złożona.

Jak widać liczby grupują się zarówno w jasne obszary/ ścieżki niezłożoności czy pierwszości, jak i ciemniejsze w których przeważać będą te bardziej złożone. Próba rzutu okiem w bardziej ogólnym planie, pokazuje, że cała spirala składa się z czterech w miarę niezależnych obszarów:

Czy można jakoś zmieścić te liczby w jednym kawałku? Ano można. Zauważmy, że każdy kolejny obieg tworzy nam kwadrat o boku równym kolejnym liczbom nieparzystym. A gdyby zastosować inną metodę dającą wzrost kwadratowy? Na przykład ułożenie liczb w piramidę:
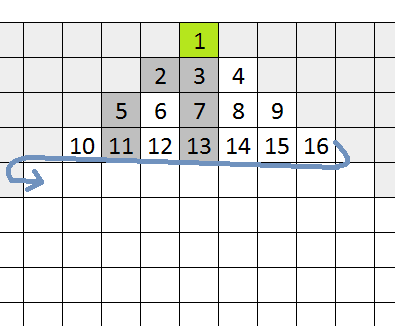
Oto obrazek, jaki udało się uzyskać:

Ta metoda marnotrawi co prawda pewien obszar rysunku, ale nie ma za to „nieciągłości”. Dla sportu zaznaczyłem jeszcze najbardziej na tym rysunku widoczną linię wzmożonej występowalności liczb pierwszych, wskazaną przez żółte strzałki. Rzecz jasna nie wszystkie liczby są w tej linii pierwsze, ale jest ich więcej niż gdzie indziej. Zaczyna się od 41 kolumny punktów (czyli od liczby 412), idąc w dół będziemy mieli kolejne: 422–1, 432–2… czyli ogólnie (41+n)2–n. Po zamianie zmiennych m=41+n dostaniemy wzór: m2–m+41, co wskaże nam liczby mniejsze od 412, a też należące do serii. Liczby pierwsze pasujące do tego wzoru zaznaczyłem na żółto. Zauważmy, że uwidoczniona linia to „połowa” jednej z formuł Eulera: 4k2–2k+41.
I to by było na tyle, jeśli chodzi o ładne obrazki od Ulama. Łatwo się je tworzy w komputerze, więc zachęcam do samodzielnej twórczości. Może ktoś wyłapie coś ciekawszego?
Inne tematy w dziale Technologie

