Całka z 1/(s^2 +1)

Aby scałkować wyrażenie 1/(s²+1) po ds trzeba mieć doświadczenie.

Dzieci w szkole uczą się najpierw mnożenia liczb naturalnych a dopiero potem na bazie tej wiedzy starają się odgadnąć wynik operacji dzielenia. Z całkowaniem jest podobnie. Trzeba wykonać wiele operacji odwrotnych jakimi są w stosunku do całkowania operacje różniczkowania aby potem próbować odgadywać wynik całkowania.

Jako, że nie mamy tutaj czasu na zdobywanie takiego doświadczenia posłużymy się doświadczeniem innych.

Ci "inni" twierdzą, że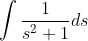  

to

(plus dowolna liczba (stała C))

Możemy sprawdzić czy ci "inni" nie wciskają nam kitu.

Sprawdzimy to poprzez zróżniczkowanie funkcji arctan(s) + C.

Pochodna liczby (stałej C) wynosi zero więc tą stałą się nie przejmujemy.

Musimy znaleźć jedynie pochodną funkcji arctan(s).

Funkcja arctan(s) jest funkcją odwrotną do funkcji tan(α) więc ich pochodne są wzajemnymi odwrotnościami gdy s=tan(α),

czyli arctan'(s) = 1 / tan'(α).

tan(α) to jest to samo co iloraz: sin(α)/cos(α),

pochodna tan(α) = pochodna sin(α)/cos(α)

czyli tan'(α) = (sin(α)/cos(α))'

Korzystając z zasady obliczania pochodnej ilorazu funkcji: (f(x)g(x))' = [f'(x)g(x) - f(x)g'(x)] / g²(x)

mamy:

tan'(α) = (sin(α)/cos(α))' = [cos(α)cos(α) - sin(α)(-sin(α))] / cos²(α)

czyli

tan'(α) = [cos(α)cos(α) + sin(α)sin(α)] / cos²(α) = [cos²(α) + sin²(α)] / cos²(α)

czyli

tan'(α) = cos²(α) / cos²(α)   +   sin²(α) / cos²(α)

czyli

tan'(α) = 1 + tan²(α).

Mamy zatem:

arctan'(s) = 1 / tan'(α) = 1 / (1 +  tan²(α))

czyli mając na uwadze, że s = tan(α)

otrzymujemy:

arctan'(s) =  1 / (1 +  s²)

Sprawdziliśmy tym samym, że  ci "inni" nas nie oszukiwali.