Dlaczego zwiększa się masa?

Spis treści
1. Wstęp
2. Wzajemne przyśpieszanie i rozbicie cząstek
    2a. Zderzenie cząstek i okrążenie
    2b. Zderzenie cząstek i rozbicie
    2c. Zderzenie cząstek i rozbicie z wymianą składnika
    2d. Wzajemne przenikanie cząstek
3. Sprężyste zderzenie cząstek - zderzenie czołowe
4. Sprężyste zderzenie cząstek - zderzenie boczne
5. Konfrontacja teorii z praktyką
6. Zakończenie

1. Wstęp
Na tytułowe pytanie można odpowiedzieć na kilka sposobów. Obecnie w naukowym świecie fizyki jest rozpowszechniony jeden sposób. Ten sposób opiera się na dwóch koncepcjach. Jedna koncepcja głosi, że energia jest równoważna masie i ta równoważność jest przeliczana zgodnie ze wzorem E=m*c^2. Druga koncepcja głosi, że energia, która jest zużywana na przyspieszenie materii, zamienia się w masę tej materii i podczas przyśpieszania kumuluje się. W oparciu o te dwie koncepcje obecnie fizycy wyjaśniają, co to jest takiego masa relatywistyczna, a do obliczania wielkości masy relatywistycznej Mr pędzącego obiektu wykorzystują wzór: Mr=Mo*c*(c^2-v^2)^(-0,5), gdzie Mo jest masą spoczynkową obiektu, v jest prędkością obiektu, c jest prędkością światła.
Na razie fizycy, nie znając szczegółowo mechanizmu takiej przemiany energii w masę i odwrotnie, muszą uważać taką interpretację i wyjaśnienie za wystarczające.

2. Wzajemne przyśpieszanie i rozbicie cząstek
Spodziewając się tego, że czytelnik wcześniej mógł nie zastanawiać się nad fundamentalnymi właściwościami składników materii, autor postara się tutaj przybliżyć te właściwości. Składniki materii są takimi dziwnymi tworami przyrody, że mamy z nimi do czynienia na co dzień, ale bardzo mało wiemy na ich temat. I dzieje się tak w sytuacji, kiedy każdy widzi, jak struktura materii przeciwstawia się zarówno przy jej rozciąganiu, jak i przy jej ściskaniu. Co to oznacza? Oznacza to, że cząstki materii są otoczone obszarami, które zapewniają im łączenie się ze sobą i tworzenie stabilnych układów strukturalnych. Każda cząstka znajdując się w tym szczególnym obszarze, należącym do sąsiedniej cząstki, i tworząc z tą sąsiadką trwałe wiązanie, doznaje przyśpieszenia, dzięki któremu jest przetrzymywana w tym obszarze. Gdy człowiek chce rozerwać takie połączenie między dwoma cząstkami, musi nadać jednej z tych dwóch cząstek przyśpieszenie, które będzie większe i przeciwnie skierowane w stosunku do przyśpieszenia, jakie tej cząstce nadaje druga, sąsiednia cząstka.
Obszary, które otaczają centra cząstek i służą do tworzenia wiązań między cząstkami, zostały nazwane potencjałowymi powłokami. Pojedyncza powłoka cząstki jest ograniczona przez dwa potencjalne zbocza - zbocze wewnętrzne otacza centrum cząstki i jest położone bliżej tego centrum, czyli ma mniejszy promień, a zbocze zewnętrzne, otaczając cząstkę, a zarazem ograniczając obszar powłoki od zewnątrz, ma większy promień.

2a. Zderzenie cząstek i okrążenie
Jeśli człowiek nada zbyt małą prędkość jednej cząstce z układu, wówczas nie dojdzie do rozerwania układu dwóch cząstek - przykład można obejrzeć korzystając z pliku PES_oderwanie0.gas.*) Tam człowiek stara się ingerować w całość układu złożonego z cząstek 1 i 2, stara się nadać przyśpieszenie cząstce 2 za pomocą cząstki 31. Przyśpieszenie jest nadawane w specyficzny sposób. Sposób ten polega na tym, że cząstka 31 porusza się z mniejszą bądź większą stałą prędkością początkową. Prędkość tej cząstki jest stała do tego momentu, aż jej centralny punkt dotrze do zewnętrznego potencjalnego zbocza powłoki cząstki 2. Gdy cząstka 31 dociera do zbocza, tam jej prędkość jest hamowana. Gdy cząstka 31 ma początkową prędkość 15 j.pr. (jednostek prędkości), to ta prędkość jest zbyt mała do pokonania zewnętrznego potencjalnego zbocza cząstki 2. Przyśpieszenie na tym zboczu hamuje ruch cząstki 31 i odrzuca ją "na zewnątrz" od centrum cząstki 2. Ten proces można zobaczyć korzystając z roboczego pliku PES_oderwanie.gas.
Pokonanie tego zbocza następuje, gdy początkowa prędkość cząstki 31 jest równa 55 j.pr. Właśnie tak dzieje się, gdy proces przebiega po uruchomieniu roboczego pliku PES_oderwanie0.gas. Teraz cząstka 31 pokonuje zewnętrzne zbocze, ale zostaje ona zahamowana przez zbocze wewnętrzne cząstki 2. Zostaje więc uwięziona w obszarze powłoki cząstki 2 i okrąża centrum cząstki 2, aby następnie opuścić tę powłokę po przeciwnej stronie.
Z tego powodu, że cząstka 31 ma promień swojego potencjalnego zbocza równy 1,5 j.dl. (jednostek długości), czyli jest mniejszy od promienia powłoki, po której porusza się okrążając centrum cząstki 2, nie może ona wpłynąć na cząstkę 2 i nadać jej przyśpieszenie. A wszystko to z tego powodu, że początkowa prędkość cząstki 31 była zbyt mała, aby mogło dojść do rozbicia układu cząstek 1 i 2.

2b. Zderzenie cząstek i rozbicie
Sytuacja zmienia się diametralnie, gdy początkowa prędkość cząstki 31, zamiast 55 j.pr., wynosi 75 j.pr. W przykładzie, który można obejrzeć za pomocą pliku PES_oderwanie1.gas, przyśpieszenie, jakie uzyskuje cząstka 2 od cząstki 31, jest wystarczająco duże, aby doszło do rozerwania układu cząstek 1 i 2. Przy prędkości cząstki 31 wynoszącej 75 j.pr., przyśpieszenie, jakie cząstka 2 przeciwstawia pędzącej cząstce za pośrednictwem swojego wewnętrznego zbocza, jest już niewystarczające.  Cząstka 31 pokonuje zatem także to zbocze. A następnie, sama jest w stanie przyśpieszyć cząstkę 2 w taki sposób, aby ją oderwać od cząstki 1. Umożliwia to zwiększona prędkość cząstki 31 oraz ten fakt, że cząstka 31 ma dziesięciokrotnie większą masę od masy cząstek 1 i 2. Do momentu pokonania obu potencjalnych zboczy cząstki 2 masa cząstki 31 nie miała istotnego znaczenia. Bo na tych zboczach innym, sąsiednim cząstkom, niezależnie od wielkości ich masy, jest nadawane to samo przyśpieszenie. Dopiero kiedy centrum cząstki 2 znalazło się w obszarze działania zbocza cząstki 31 (o promieniu 1,5 j.dl.), wówczas doszło do przyśpieszania cząstki 2 i do rozerwania jej strukturalnej więzi z cząstką 1. Dopiero wówczas w przebiegu procesu przyśpieszania stała się decydująca wielkość masy cząstki 31.

2c. Zderzenie cząstek i rozbicie z wymianą składnika
Interesujący jest także w pewnym sensie pośredni przypadek, który jest związany z rozbiciem układu cząstek 1 i 2. W tym przypadku dochodzi do rozbicia układu cząstek 1 i 2, ale cząstki nie rozlatują się w różne strony. Bo w tym przypadku cząstka 2 zostaje wyrzucona z układu, ale jej miejsce zajmuje cząstka 31. Z tym przypadkiem można zapoznać się korzystając z roboczego pliku PES_oderwanie2.gas.
W tym przypadku interesujące może być to, że wyrzucona z układu cząstka 2 o masie m(2)=1000 j.m. (jednostek masy) zostaje zastąpiona przez cząstkę 31 o masie m(31)=10000 j.m.

2d. Wzajemne przenikanie cząstek
Oderwanie cząstki 2 i rozbicie układu stało się możliwe dlatego, że prędkość cząstki 31 spełniała określone warunki. Ta prędkość nie była zbyt mała, ale także nie była zbyt duża. Bo przy dostatecznie dużej prędkości dochodzi do tego, że cząstka 2 przenika przez potencjalną barierę zbocza, pędzącej z dużą prędkością, cząstki 31. Inaczej mówiąc, przyśpieszenie, jakie cząstka 2 w tym przypadku uzyskuje na potencjalnym zboczu cząstki 31, jest mniejsze od przyśpieszenia, jakie cząstka 2 uzyskuje na potencjalnym  zboczu cząstki 1. Dzięki temu cząstka 2 nie opuszcza obszaru potencjałowej powłoki cząstki 1 i nie dochodzi do rozbicia układu dwóch cząstek. Czyli wówczas dochodzi do wzajemnego przenikania się cząstek, a nie do rozbicia strukturalnego układu. Takie przeniknięcie staje się możliwe dopiero przy znacznej początkowej prędkości cząstki 31, na przykład, równej 5500 j.pr. Przy tej prędkości następuje wzajemne przenikane cząstek, a wówczas cząstka 31 nie niszczy układu cząstek 1 i 2, a jedynie nadaje temu układowi jako całości pewną prędkość ruchu i pewną energię, która istnieje w postaci drgań cząstek 1 i 2 względem siebie.
Wzajemne przenikanie się cząstki 31 z układem cząstek 1 i 2 można obejrzeć na komputerowym modelu korzystając z pliku PES_oderwanie3.gas.

3. Sprężyste zderzenie cząstek - zderzenie czołowe
Sprężyste zderzenie cząstek było już częściowo przedstawione powyżej. Ale tutaj to zderzenie cząstek będzie przedstawione w wersji klasycznej, w której to wersji jest ono także nazywane "zderzeniem czołowym". Aby należycie zrozumieć mechanizm zderzenia dwóch cząstek, należy skorzystać z plików: PES70.1.gas, PES70.2.gas, PES70.1_m02.gas, PES70.2_m02.gas.
Czołowe zderzenie można przedstawić za pomocą dwóch jednakowych cząstek o masie m=1000 j.m. (jednostek masy) oraz/lub dwóch jednakowych cząstek o masie m=1002 j.m., z których jedna cząstka (z numerem 1) jest nieruchoma, a druga cząstka (z numerem 31) mknie w kierunku pierwszej cząstki z pewną prędkością początkową. Charakter zderzenia takiej pary cząstek zależy od prędkości, z jaką cząstka 31 pędzi w kierunku cząstki 1. Gdy cząstka 31 ma początkową prędkość 70,1 j.pr. (lub mniejszą prędkość), to gdy zbliży się ona do cząstki 1 na odległość w przybliżeniu równą promieniowi zewnętrznego potencjalnego zbocza, to wówczas wskutek procesu zderzenia zatrzyma się, a jej energię ruchu (prędkość)  przejmie cząstka 1. Dzieje się tak zarówno w przypadku pary cząstek z masą 1000 j.m., jak i pary cząstek z masą 1002 j.m.
Ale gdy podobne doświadczenie zostanie wykonane dla pary cząstek o masie 1000 j.m., a przy tym cząstka 31 będzie miała powiększoną początkową prędkość do wartości 70,2 j.pr., to nie będzie sprężystego zderzenia cząstek. Korzystając z pliku PES70.2.gas można na komputerowym modelu obserwować, jak następuje wzajemne przenikanie się cząstek. W trakcie tego procesu przenikania cząstka 1 zostanie jedynie nieznacznie przesunięta w kierunku ruchu cząstki 31 i otrzyma nieznaczną prędkość, przy czym nastąpi nieznaczna zmiana prędkości ruchu cząstki 31 i będzie ona dalej poruszała się z prędkością zbliżoną do wartości 70,2 j.pr. Oczywiście, dalsze powiększanie początkowej prędkości cząstki 31 w kolejnych doświadczeniach z dwoma cząstkami również będzie skutkować wzajemnym przenikaniem się cząstek.

Wzajemne przenikanie się cząstek o masie 1000 j.m. jest związane z tym, że przyśpieszenia, jakie nadają sobie wzajemnie cząstki 1 i 31 oddziałując na sąsiadkę swoim potencjalnym zboczem, są niewystarczające do tego, aby przy danej prędkości 70,2 j.pr. mogły one przekazać sobie energię ruchu. Inaczej mówiąc, masa tych cząstek jest zbyt mała, aby mogło dojść do skutecznego wyhamowania ruchu cząstki 31 i nadania (w tym samym kierunku) ruchu cząstce1. Ta fizyczna prawda ujawnia się już w kolejnym modelowanym doświadczeniu, które można obejrzeć na ekranie komputera po uruchomieniu pliku PES70.2_m02.gas. Zapisane w tym pliku wszystkie początkowe parametry pozostaną takie same, a jedynie masa cząstek jest powiększona do 1002 j.m. Skutek zderzenia tej pary cząstek jest taki, jaki powinien być przy sprężystym czołowym zderzeniu.

Inaczej mówiąc, w czołowym sprężystym zderzeniu dwóch cząstek o masie m=1000 j.m. zwiększanie początkowej prędkości cząstki 31 (w kolejnych doświadczeniach) daje efekt w postaci sprężystego zderzenia jedynie do pewnej granicznej prędkości. Jeśli początkową prędkość cząstki 31 oznaczyć jako Vo, a prędkość cząstki 1 po zderzeniu jako Vc, to na wykresie wygląda to następująco.

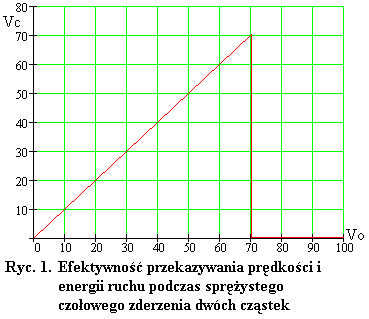
Gdy w kolejnych doświadczeniach cząstka 31 ma prędkość przekraczającą tę graniczną początkową prędkość (w przybliżeniu równą) 70,1 j.pr., to za każdym razem będzie to skutkować wzajemnym przenikaniem cząstek. Jeśli wcześniej skuteczność przekazywania prędkości ruchu między cząstkami odbywała się zgodnie z prawami dynamiki Newtona i wynosiła 100%, a przy tym po zderzeniu prędkość Vc cząstki 1 była prawie równa prędkości Vo cząstki 31, jaką ona miała przed zderzeniem, to nagle po przekroczeniu granicznej prędkości - Vo równej około 70,1 j.pr. - prędkość Vc staje się niemal zerowa. Cząstka 31 przenika przez cząstkę 1 i mknie dalej z niemal niezmienioną prędkością.

4. Sprężyste zderzenie cząstek - zderzenie boczne 
Do zderzenia bocznego cząstek 31 i 1 dochodzi wówczas, gdy centrum cząstki 1 nie znajduje się na linii, wzdłuż której porusza się cząstka 31. Ale na linia znajduje się obszar potencjalnego zbocza cząstki 1.
Z serią takich modelowych doświadczeń można zapoznać się korzystając z plików, które są wymienione poniżej.

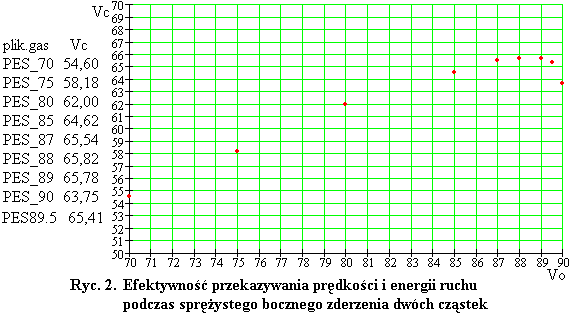
W nazwie każdego z tych plików zapisana jest początkowa prędkość cząstki 31, na przykład, w pliku PES_70.gas prędkość początkowa Vo=70 j.pr. Obok jest zapisana wartość prędkości Vc, z jaką porusza się cząstka 1 po zderzeniu - w przypadku tego zderzenia Vc=54,60 j.pr. Wyniki tej serii doświadczeń są przedstawione obok na punktowym wykresie Ryc. 2.

W poniższym wykazie są przedstawione parametry cząstek 31 i 1, jakie mają one po zderzeniu przy szerszym zakresie początkowej prędkości cząstki 31. Teraz zakres początkowej prędkości cząstki 31 mieści się między 0,1 j.pr. i 200 j.pr.  Na podstawie tych wyników można stwierdzić, że procesy zderzenia w każdym przypadku przebiegają zgodnie z fizycznymi prawami mechaniki klasycznej.

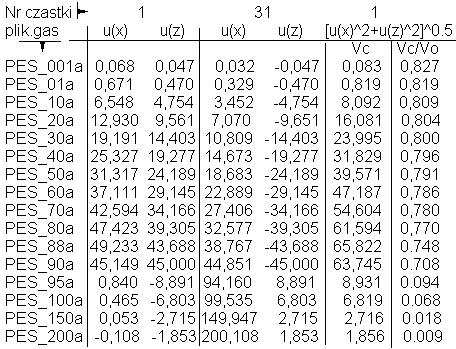
Dzięki temu, że masy cząstek 31 i 1 - albo inaczej, współczynniki proporcjonalności w matematycznej funkcji natężenia pola cząstek w obszarach ich potencjałowych powłok - są jednakowe, można łatwo stwierdzić, że suma pędów cząstek przed i po zderzeniu jest taka sama. A dzieje się tak dlatego, że suma prędkości cząstek wzdłuż osi X przed i po zderzeniu jest taka sama. Taka sama jest także prędkość wzdłuż osi Z - przed zderzeniem i po zderzeniu suma prędkości wynosi zero.

Korzystając z danych z powyższego wykazu parametrów, można sprawdzić, że także suma energii kinetycznej cząstek nie zmienia się w wyniku zderzenia. Poniżej są przedstawione wyniki takiego sprawdzenia dla zderzeń, których końcowe parametry zostały zapisane w plikach PES_40a.gas, PES_90a.gas i PES_150a.gas.

Z powyższego wynika, że zderzenie boczne dwóch cząstek jest zderzeniem sprężystym w identycznym sensie, jak zderzenie czołowe. I gdy w kolejnych doświadczeniach będzie powiększana początkowa prędkość cząstki 31, z tej samej przyczyny odbywa się nagły spadek energii, jaka jest przekazywana w trakcie zderzenia. Różnica jest tylko taka, że przy bocznym zderzeniu spadek ilości przekazywanej prędkości i energii od cząstki 31 do cząstki 1 jest mniej gwałtowny. Punktowy wykres zmian wartości przekazywanej prędkości ruchu między cząstkami 31 i 1 pokazany jest poniżej.

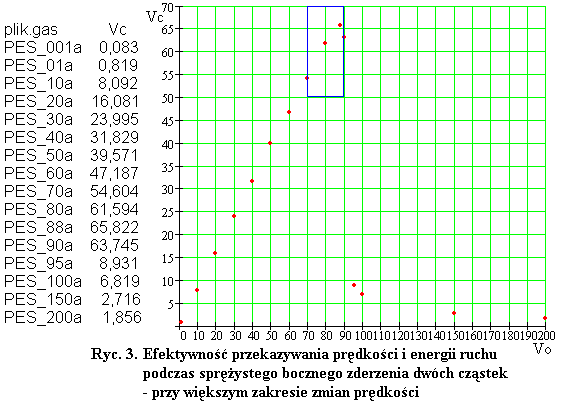
Obejmuje on większy zakres zmienności Vo i Vc, aniżeli przedstawiony wcześniej wykres punktowy Ryc. 2 - pole zmienności wykresu punktowego z Ryc. 2 jest zaznaczone niebieską ramką.

5. Konfrontacja teorii z praktyką
Pora postawić pytanie: jak w rzeczywistości przedstawia się sprawa z tą masą - czy rzeczywiście wskutek wzrostu prędkości cząstek zwiększa się ich masa? W którym miejscu bądź w jakiej sytuacji w przedstawianych doświadczeniach miałby następować wzrost masy? Jeśli ten wzrost masy w ogóle miałby następować, to musiałby on dotyczyć cząstki 31, bo to ona w różnych doświadczeniach ma coraz większą prędkość. Ale należy pamiętać, że powyżej nie były przedstawiane rzeczywiste zjawiska, tylko ich modele. A w modelach zjawisk cząstce 31 można przypisywać dowolnie duże początkowe prędkości i w żaden sposób nie będzie to powiązane ze wzrostem masy. Zatem w tym miejscu można mieć zastrzeżenia co do tego, czy takie modelowanie ma cokolwiek wspólnego z rzeczywistymi zjawiskami.

Tytuł artykułu - Dlaczego zwiększa się masa? - może wydawać się nie na miejscu. Obiecuje on wyjaśnienie tego fenomenu, ale w artykule takiego wyjaśnienia dotychczas nie było. Pora zatem na końcowe wyjaśnienia. Otóż tytuł, jak i sam artykuł, powinien dotyczyć wzrostu masy. Bo tylko w taki sposób można nawiązać do nielogicznych - bo niezgodnych z doświadczalnymi faktami - zapisów w dzisiejszej teoretycznej fizyce. Wymienione we wstępie zależności: E=m*c^2 i Mr=Mo*c*(c^2-v^2)^(-0,5), zostały wymyślone bez związku z doświadczalnymi faktami, które zostały przedstawione w artykule. Te fakty doświadczalne to przede wszystkim procesy związane ze zderzaniem się cząstek oraz ich wzajemnym łączeniem się w materialne struktury. Podczas zderzeń następuje przekazywanie między cząstkami prędkości ruchu oraz związanej z tym ruchem energii kinetycznej cząstek.

Wymienione dwie matematyczne zależności, opisujące E oraz Mr,  nie mają związku z doświadczalnymi faktami przede wszystkim z tego powodu, że obecnie akademicka teoretyczna fizyka przy opisie wiązań strukturalnych materii posługuje się pojęciem energii, ale nie opisuje, czym jest ta energia, czym jest materia i w jaki sposób powstają wiązania między składnikami materii.

W artykule jest opisanych szereg doświadczalnych faktów, którymi powinna być zainteresowana teoretyczna fizyka. Bo jest przedstawiony mechanizm powstawania wiązań strukturalnych, mechanizm zderzeń, jakie zachodzą między cząstkami, mechanizm wymiany składników strukturalnych, mechanizm wzajemnego przenikania się cząstek. W przedstawionym tu opisie zjawisk i mechanizmów ich przebiegu w oczywisty sposób ujawnia się fizyczna istota i obraz składników materii oraz związanej z nimi energii. Ujawnia się także nierozerwalny związek energii z materią. Ujawnia się przy tym niedorzeczność poglądu, że energia jest równoważna materii, że następuje zamiana energii w masę materii i że w ogóle istnieje masa relatywistyczna.**)

Najważniejsze jednak jest to, że przedstawiony jest mechanizm zderzeń, który skutkuje przekazywaniem energii jedynie do pewnej granicznej prędkości poruszania się jednych cząstek względem drugich. Kiedy ta graniczna prędkość zostaje przekroczona, składniki materii wywierają na siebie coraz mniejszy wpływ i w końcu wzajemnie przenikają się, niemal nie przekazując sobie nawzajem swojej energii kinetycznej.

Konfrontując tę wiedzę z tym, co dzieje się w akceleratorach cząstek, trzeba tu przypomnieć mechanizm przyśpieszania cząstek. Przyśpieszanie cząstek w akceleratorze odbywa się w odpowiednio skonstruowanej strefie. Niezależnie od budowy tej strefy, czyli przyśpieszacza, i stosowanej metody przyśpieszania cząstek, przyśpieszanie zawsze odbywa się na zasadzie przekazywania energii ruchu od jednych cząstek do drugich. Przyśpieszanie zawsze odbywa się tak, że energia ruchu cząstek - które składają się na strukturę materii przyśpieszacza i są w tej strukturze pobudzane do ruchu - jest przekazywana cząstkom, które mają w tym procesie uzyskać dużą prędkość ruchu w określonym kierunku. Sposób pobudzania do ruchu cząstek składowych materii przyśpieszacza jest dla przebiegu procesu przyśpieszania mało istotny.  Sposób ten może być mniej lub bardziej efektywny. Pobudzanie do ruchu składowych cząstek materii przyśpieszacza ma swój odpowiednik w przedstawianych tutaj komputerowych modelach procesów. Tym odpowiednikiem jest początkowa prędkość ruchu cząstki 31.

Przekazywanie energii ruchu od składowych cząstek strukturalnych przyśpieszacza do cząstek, które mają uzyskać w akceleratorze dużą prędkość, odbywa się za pośrednictwem ogromnej ilości cząstek pośrednich. Z tego powodu jest to proces niezwykle złożony pod względem ilości zderzeń cząstek pośrednich i kierunków ich ruchu. Ta złożoność procesu przekazywania energii wpływa na końcową efektywność przyśpieszania cząstek w akceleratorze. Ten wpływ wyraża się w ten sposób, że efektywność przekazywania energii nie zmienia się skokowo, tak jak to jest pokazane na Ryc. 1, lecz w sposób płynny, czyli tak jak na Ryc. 2.

6. Zakończenie
Powyżej zostały przedstawione fizyczne procesy, takie jak powstawanie wiązań między cząstkami, zderzenia między nimi, wymiana składników strukturalnych, wzajemne przenikanie się cząstek. Te procesy istnieją w rzeczywistości. Ale w tych procesach w ogóle nie ma miejsca na wzrost masy cząstek materii - zjawisko to nie istnieje w procesach fizycznych.
Ludzie, którzy posługują się pojęciem wzrostu masy materii, który (to wzrost masy) jest spowodowany dużą prędkością ruchu tej materii, po prostu nie wiedzą, o czym mówią. Mają oni wiedzę o trudnościach, jakie pojawiają się podczas przyśpieszania cząstek materii do coraz większych prędkości, ale błędnie tłumaczą sobie i innym przyczynę istnienia tych trudności. Ten błąd popełniają oni dlatego, że nie wiedzą o istnieniu w przyrodzie fizycznego prawa - prawa znikomego działania składników materii na inne składniki przy ich bardzo dużej względnej prędkości ruchu.
Więcej o tym fizycznym prawie można przeczytać w artykule "Prawo znikomego działania i związane z nim zjawiska" na http://pinopa.republika.pl/05_ZakonND.html.
____________________________________

*) Aby poprawnie rozumieć treść artykułu, niezbędne jest zapoznanie się z parametrami cząstek oraz przebiegiem wzajemnych oddziaływań między nimi. Parametry cząstek oraz obrazy przebiegających procesów można oglądać na ekranie komputera. Początkowe parametry cząstek są zapisane w plikach roboczych formatu gas. Otworzyć te pliki i uruchomić bieg procesów można za pomocą modelującego programu komputerowego Gas2n.exe. Modelujący program oraz pliki robocze można skopiować na pinopapliki2.republika.pl/Gas2n.zip.
Uwaga 1: Komputerowe programy modelujące, które można skopiować na "stronie pinopy", pracują poprawnie na komputerach z systemami Windows ME i Windows XP. Możliwe, że współpracują poprawnie także z innymi systemami Windows, ale to wymaga sprawdzenia.
Uwaga 2: Aby oglądać przebiegające procesy oddziaływań między cząstkami, po otwarciu programu Gas2n.exe należy:
1. w tablicy "Formula" uaktywnić działanie matematycznej funkcji PES - ta funkcja w programie steruje przyśpieszeniem, jakie każda cząstka nadaje swoim sąsiadkom, gdy znajdują się one na jej potencjałowej powłoce;
2. uaktywnić przycisk "Show Listing" - pozwala to obserwować zmiany parametrów procesu w postaci położenia cząstek w układzie XYZ oraz prędkości tych cząstek. Poza tym, uaktywnienie "Show Listing" w znaczący sposób zmniejsza prędkość biegu modelowanego procesu, co umożliwia jego obserwację na ekranie.
Przełączanie obserwowanych parametrów na tablicy "Listing" - wartości współrzędnych cząstek w układzie XYZ na wartości prędkości cząstek albo odwrotnie - odbywa się po dwukrotnym kliknięciu lewym klawiszem myszki przy położeniu wskaźnika na białym polu tablicy "Listing".

**) Zapoznanie się z kodem programu Gas2n.exe daje możliwość sprawdzenia, że przedstawiona na wykresach skokowa zmiana Vc, istniejąca przy wzroście Vo, nie jest skutkiem wzrostu masy. Kopia tego kodu jest zapisana w pliku Gas2n_Main.html na pinopapliki2.republika.pl/Gas2n.zip.
________________________________
Bogdan Szenkaryk "Pinopa"
Polska, 2015.12.20.