Przedstawiana poniżej matematyczna ciekawostka polega na... tego nie trzeba chyba szczegółowo wyjaśniać. Wystarczy popatrzeć na dwa poniższe rysunki i przeanalizować przedstawione na nich matematyczne zależności. Ale pewne detale tej ciekawostki opiszę i wyjaśnię.

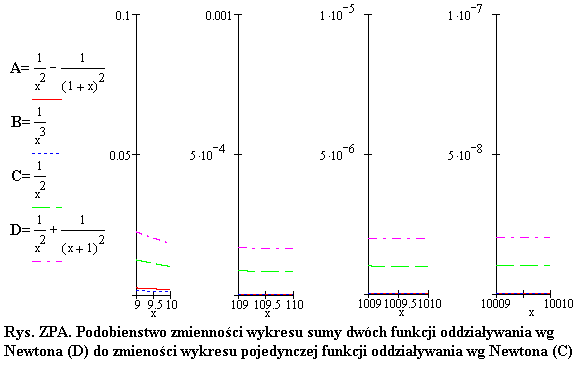
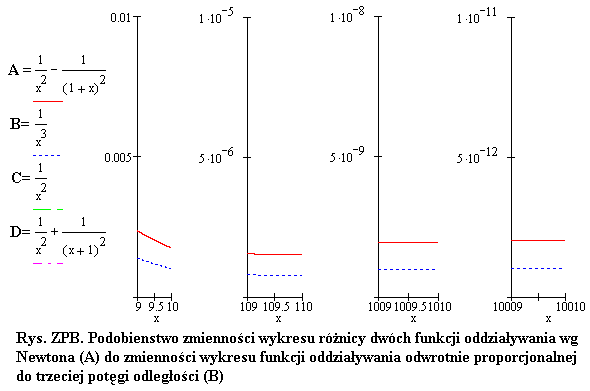
Na rysunkach są przedstawione matematyczne funkcje i ich wykresy. Na obu rysunkach są przedstawione te same funkcje. Ale wykresy tych funkcji sa przedstawione w takich skalach, że na Rys.ZPA jest pokazana zmienność sumy dwóch funkcji (D), z których każda zmienia się odwrotnie proporcjonalnie do kwadratu odległości, natomiast na Rys. ZPB widoczna jest zmienność różnicy dwóch tych samych funkcji (A). Na na Rys. ZPA zmienność funkcji (D) można porównać ze zmiennością funkcji (C) i można zobaczyć, że przebiega ona w taki sposób, który jest potwierdzany przez wiele faktów doświadczalnych. Jakie to są fakty doświadczalne? Najprostszy doświadczalny fakt zawiera się we wzorze Newtona, który opisuje siłę grawitacyjnego oddziaływania ze sobą dwóch ciał, czyli 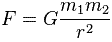
 . W tym wzorze siła oddziaływania grawitacyjnego jednego ciała na drugie ciało, na przykład, na ciało próbne, jest wprost proporcjonalna do masy tego pierwszego ciała. Przy podwojeniu masy ciała następuje podwojenie siły oddziaływania tego ciała na ciało próbne.
. W tym wzorze siła oddziaływania grawitacyjnego jednego ciała na drugie ciało, na przykład, na ciało próbne, jest wprost proporcjonalna do masy tego pierwszego ciała. Przy podwojeniu masy ciała następuje podwojenie siły oddziaływania tego ciała na ciało próbne.
Na drugim rysunku jest pokazana zmienność różnicy dwóch funkcji (A), z których każda jest odwrotnie proporcjonalna do kwadratu odległości. W tym przypadku (ta różnica funkcji) zmienia się w podobny sposób, jak funkcja zmieniająca się odwrotnie proporcjonalnie do sześcianu (do trzeciej potęgi) odległości, czyli podobnie jak funkcja (B).
Ta matematyczna ciekawostka ma bezpośredni związek z fizyką. Bo odwrotnie proporcjonalnie do kwadratu odległości w naturze zmieniają się, oprócz oddziaływań grawitacyjnych, także oddziaływania magnetyczne i oddziaływania elektrostatyczne. Z fizycznych doświadczeń wiadomo, w jaki sposób sumują się oddziaływania grawitacyjne, magnetyczne bądź elektrostatyczne. Mianowicie, sumują się one w taki sposób, że sumaryczny charakter oddziaływania nie ulega zmianie. Czyli, po zsumowaniu ich wpływ na otoczenie nadal zmienia się według funkcji, która jest odwrotnie proporcjonalna do kwadratu odległości. A może nie zawsze tak się dzieje? Może są potrzebne dodatkowe badania, aby sprawdzić, czy tak rzeczywiście przebiegają oddziaływania w naturze?
A czym szczególnym miałaby wyróżniać się opisywana ciekawostka? Ano, podpowiada ona, że w dziedzinie fizycznych oddziaływań między składnikami materii nie wszystko jest takie proste, jak na pozór to się wydaje. Bo w przypadku sumowania i odejmowania fizycznych oddziaływań, ze szczególnym położeniem nacisku na odejmowanie oddziaływań, można na to zagadnienie spojrzeć z dwóch różnych punktów widzenia. Bo zmniejszanie fizycznego oddziaływania może następować w wyniku odrzucenia (z rozpatrywanego procesu) tego składnika, który wcześniej był dodany do układu. W takim przypadku matematyczne "odejmowanie" jest jedynie formalną czynnością, którą można by nazwać "rezygnacją z dodawania". Po takim "odejmowaniu" układ i jego oddziaływanie, pod względem charakteru tego oddziaływania i jego zależności od odległości, pozostaje w tym samym stanie.
Inny sposób odejmowania polega na sumowaniu ze sobą dwóch składników, z których jeden ma przeciwne fizyczne właściwości względem właściwości drugiego składnika. W fizyce takie przeciwne właściwości są oznaczane symbolicznie znakami "+" i "-". Oddziaływanie takich składników na postronny, trzeci składnik jest przeciwne, czyli gdy jeden z nich przyciąga trzeci składnik, to drugi go odpycha.
I właśnie ten drugi przypadek odejmowania jest matematycznie zapisany na powyższych rysunkach jako zależność A=(1/x^2)-(1/(x+1)^2). Ten właśnie przypadek odejmowania się przeciwstawnych oddziaływań podsuwa myśl, że w fizyce istnieją zależności, które wymagają sprawdzenia, czy rzeczywiście są one takimi zależnościami, za jakie były dotychczas uważane. Bo w fizyce - choć wiele w niej mówi się o przeciwnych właściwościach, na przykład, cząstek materii - nie jest znana taka sytuacja, aby wskutek nakładania się oddziaływań dochodziło do zamiany odwrotnej proporcjonalności do kwadratu odległości na odwrotną proporcjonalność do sześcianu odległości. A przedstawiane obecnie w fizyce właściwości, które są symbolicznie oznaczane znakami "+" i "-" wskazują na to, że właśnie do takiej zamiany powinno dochodzić.
_______________________
Bogdan Szenkaryk "Pinopa"
Polska, Legnica, 2014.05.02.
Jestem wszystkim, wszędzie i zawsze. I wy wszyscy - także, tylko jeszcze o tym nie wiecie. Odkryjcie to na http://pinopa.narod.ru/Polska.html. Przekazuję prośbę od Łukasza - lukasz@lukasz.sos.pl : Bardzo proszę o 1,5 procent, Was nic nie kosztuje poza wypełnieniem dwóch pól w zeznaniach PIT, a mi ratuje życie. Proszę przekażcie ulotki swoim znajomym. Darowizny: FUNDACJA AVALON - Bezpośrednia Pomoc Niepełnosprawnym 62 1600 1286 0003 0031 8642 6001 BNP PARIBAS Fortis Bank Polska S.A. Bardzo ważny jest dopisek: SOSNA,711 (1,5%) Podatek: KRS: 0000270809 Bardzo ważny jest dopisek: SOSNA,711 PS. Jeżeli znacie firmę, która jest gotowa umieścić mój baner na swojej stronie z przekazaniem 1,5%, również proszę o kontakt. BARDZO DZIĘKUJĘ http://lukasz.sos.pl
Nowości od blogera
Inne tematy w dziale Technologie

