Oszukane umysły fizyków XX w.

Mamy już XXI wiek. Dzisiaj fizycy nie muszą czuć się odpowiedzialni za błędy, jakie zostały popełnione w ubiegłym wieku. Na przeszłość powinni spojrzeć z dystansem i starać się zrozumieć, na czym polegały błędy fizyków XX w. Nie jest to łatwe, bo przecież te błędy trzeba przypisywać ludziom, którzy dotychczas byli i są nadal uważani za autorytety naukowe. Bo trzeba przy tym stwierdzić, że autorytet się mylił, że nie dostrzegał własnych błędów. Bo trzeba podważać autorytet i stanąć ponad nim.

Zanim zobaczymy, w jaki sposób zostały oszukane umysły fizyków XX wieku, spójrzmy na poniższy rysunek. Na rysunku jest przedstawiony zrzut z ekranu komputera, na którym (to komputerze) za pomocą modelującego programu Drawer.exe były modelowane sytuacje z oddziałującymi ze sobą (w sensie grawitacyjnego oddziaływania) dwoma ciałami. Jedno ciało ma masę m=1 j.m. (jednostek masy) i jest rodzajem ciała próbnego, które porusza się niedaleko od ciała mającego wielokrotnie większą masę M. Taka sytuacja powtarza się w kilku ćwiczeniach i w każdym z tych ćwiczeń próbne ciało porusza się w tym samym kierunku i w tej samej odległości względem ciała M. Masywne ciało M ma początkową prędkość równą zero, natomiast ciało m ma pewną prędkość początkową. Gdyby nie było w pobliżu masywnego ciała M, to ciało m poruszałoby się wzdłuż trajektorii, która na rysunku jest oznaczona linią przerywaną. 

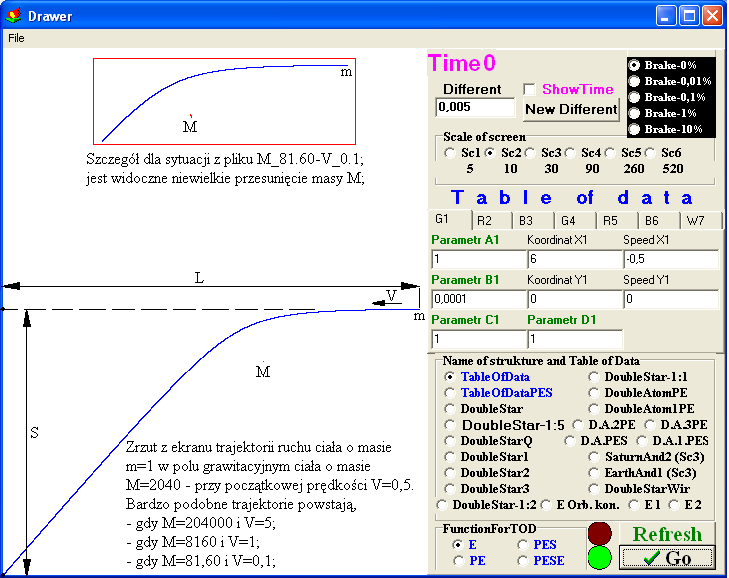
Gdy masywne ciało ma masę M=8160 j.m. (jednostek masy), a ciało próbne ma początkową prędkość V=1 j.pr. (jednostek prędkości), to wówczas trajektoria ma taki kształt, jak przedstawiony na rysunku. Dalsze ćwiczenia z programem polegały na zmianie początkowej prędkości V ciała próbnego m i takiej zmianie masy ciała M (odpowiednio do tej prędkości), aby ciało próbne nadal poruszało się w przybliżeniu po tej samej trajektorii.

I tak, gdy ciało próbne miało początkową prędkość pięć razy większą, czyli gdy V=5 j.pr., to wówczas, aby uzyskać podobny kształt trajektorii, masa ciała M musiała być 25 razy większa, czyli M=204000 j.m. Wykonano jeszcze dwa ćwiczenia, w których początkowa prędkość próbnego ciała była dziesięć razy mniejsza od powyżej podanych prędkości początkowych, czyli w jednym przypadku początkowa prędkość V=0,1 j.pr., a w drugim przypadku V=0,5 j.pr. Wówczas, w tych dwóch przypadkach, aby uzyskać podobną trajektorię ruchu ciała próbnego, masywne ciało musiało mieć masę równą odpowiednio M=81,60 j.m. i M=2040 j.m.

Poniżej podane są zależności między parametrami, jakie istnieją między drogą ruchu L ciała próbnego biegnącą równolegle do osi X, początkową prędkością V, czasem ruchu t ciała próbnego oraz wielkością przesunięcia S, która jest spowodowana grawitacyjnym wpływem ciała M. Ta wielkość przesunięcia S, w odległości L od początkowego położenia próbnego ciała m i położonego prostopadle do osi X, może przyjmować różne znaczenia. Bo jest ona zależna od relacji między wartościami masy M i początkowej prędkości próbnego ciała. Ale przeprowadzone ćwiczenia z ciałami M i m miały określony cel - celem było znalezienie odpowiadających sobie wielkości masy M i początkowej prędkości V ciała próbnego, przy których ciało próbne m porusza się po tej samej (w przybliżeniu) trajektorii. 

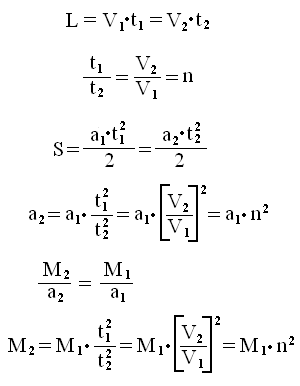
Wielkość przesunięcia S została przedstawiona we wzorze w sposób uproszczony. A mianowicie, została ona przedstawiona przy założeniu, że na ciało próbne (na drodze przesunięcia S) działa pewne średnie przyśpieszenie o stałej wartości a. Z powodu uproszczenia został pominięty fakt, że w początkowej prędkości V można wyznaczyć prędkość składową, która w tym układzie będzie początkową prędkością względem ciała M.

Istnieje także uproszczenie w wyliczeniu (określeniu) czasu t, jaki występuje we wzorze na drogę L. Bo w rzeczywistości ten czas zależy także od wpływu ciała M.

Ale jak widać, taka zamiana i uproszczenie nie zmienia relacji między parametrami.

W wyprowadzonym teoretycznie końcowym wzorze relacja jest taka sama, jak ta, która występowała w przeprowadzonym praktycznym ćwiczeniu komputerowym. A konkretnie, gdy prędkość ciała próbnego jest n-krotnie większa, to wówczas, aby uzyskać tę samą trajektorię ruchu ciała próbnego w grawitacyjnym polu ciała M, ciało M musi mieć masę większą n-krotnie do kwadratu.

Fizyka klasyczna uczy, że siła F=m*a, gdzie a - przyspieszenie, m - masa przyspieszanego ciała, a także uczy, że energia (albo praca) E=F*S, gdzie S - droga, na jakiej działa siła.

Można zapisać energię jako E=m*a*S. Ten wzór możemy skojarzyć z energią, jaka jest zużywana w przedstawionych powyżej ćwiczeniach na przemieszczenie ciała o masie m na drodze S w różnych sytuacjach. Te sytuacje różnią się między sobą tym, że gdy w jednym przypadku ciało m porusza się z prędkością V, to w drugim przypadku to samo ciało m porusza się z prędkością V*n.

Na podstawie przeprowadzonych ćwiczeń można zapisać, że gdy w jednym przypadku do przemieszczenia ciała m na drodze S wystarczało grawitacyjne oddziaływanie ciała o masie M i nadawane przez to ciało średnie przyśpieszenie a, to w drugim przypadku masa ciała musiała wynosić M*n^2, a nadawane przez to ciało przyśpieszenie musiało wynosić a*n^2. Z tego wynika, że w tym pierwszym przypadku dla przemieszczenia ciała m na drodze S byłoby niezbędne zużytkowanie energii E, natomiast w drugim przypadku musiałaby być zużyta energia E*n^2.

W pierwszym przypadku przekazywanie energii na drodze S trwałoby przez pewien czas t. W tym przypadku podczas tego procesu jego moc wynosiła E/t. W drugim przypadku czas przekazywania energii trwał t/n, natomiast moc procesu wynosiła (E/t)*n^3.

Przedstawione ćwiczenia i ich wyniki pozwalają wyciągnąć pewne wnioski. Pierwszy wniosek jest taki, że w trakcie przeprowadzonych ćwiczeń przejawiało się prawo przyrody, które nazywa się: Prawo znikomego działania. To prawo zostało opisane w 2006 roku w artykule "Prawo znikomego działania i związane z nim zjawiska" i można z nim zapoznać się na http://pinopa.narod.ru/05_ZakonND_pl.pdf. W przedstawionych komputerowych ćwiczeniach sednem było to, aby likwidować skutek działania tego prawa - i skutek działania tego prawa był likwidowany. Skutek działania tego prawa występował w postaci coraz mniejszego zakrzywiania się trajektorii ruchu ciała m w pobliżu masywnego ciała M z powodu coraz większej prędkości początkowej ciała m. Usuwanie tego skutku odbywało się w taki sposób, że była powiększana wielkość masy ciała M. A konkretnie, skuteczność prawa znikomego działania, jaka występuje przy n-krotnym wzroście prędkości ciała m, była likwidowana w taki sposób, że wielkość masy ciała M była zwiększana n-krotnie do potęgi drugiej.

Na podstawie wyników, jakie uzyskano w ćwiczeniach, można oceniać skuteczność prawa znikomego działania. Bo uzyskane wyniki wskazują, że przy n-krotnym wzroście prędkości ciała m względem ciała M, skuteczność przejawiania się prawa znikomego działania zwiększa się n-krotnie do potęgi drugiej. Czyli przejawianie się prawa znikomego działania zwiększa się w takim samym stopniu, w jakim musi powiększać się skuteczność przyczyny, która potrafi likwidować jego skutki.

Drugi wniosek wymaga zupełnie nowego spojrzenia na procedurę zmiany masy ciała M, jaka była zastosowana w przedstawionych komputerowych ćwiczeniach. Na ciało M, razem z zastosowaną w ćwiczeniach procedurą zmiany wielkości masy, można spojrzeć jak na urządzenie, za pomocą którego można przyśpieszać niewielkie ciała albo cząstki. Zamiast ciała M i zastosowanej względem niego procedury, wyobraźmy sobie, że w tym miejscu jest urządzenie, które fizycy znają jako akcelerator. Taki przyspieszacz cząstek jest urządzeniem technicznym. Przyśpiesza on cząstki i to przyspieszanie odbywa się zgodnie z prawami przyrody. Czyli podczas działania akceleratora, niezależnie od metody przyspieszania cząstek, także przejawia się prawo znikomego działania.

Na podstawie wyników ćwiczeń można wnioskować, że do utrzymania cząstek na tej samej kołowej trajektorii w akceleratorze przy n-krotnym zwiększeniu ich prędkości wymagane jest n-krotnie do kwadratu większe zużycie energii. Taki akcelerator musi mieć duży zapas mocy, bo w takiej sytuacji moc urządzenia musi być większa n-krotnie do potęgi trzeciej.

Należy tu mieć na uwadze również to, że podczas każdego ćwiczenia przesunięcie ciała m na drodze S było związane z nadaniem mu odpowiedniej prędkości w kierunku, w którym następowało przesunięcie. Ta nowo nadana prędkość w kierunku przesunięcia S musiała być odpowiednia i proporcjonalna do prędkości początkowej V ciała m. Bo dopiero wówczas był osiągany pożądany skutek w takiej postaci, że ciało m poruszało się po zaplanowanej trajektorii. Należy to mieć na uwadze zwłaszcza z tego powodu, że nawet liniowy ruch cząstek w liniowym akceleratorze wymaga przekierowania ruchu cząstek, które wcześniej, czyli na początku procesu przyspieszania, wcale nie poruszają się w tym kierunku, w którym celowo mają być przyspieszane.

Wymienione tu zależności są oczywiste, ale dopiero wówczas są oczywiste, gdy znany jest mechanizm ich powstawania. Gdy mechanizm nie jest znany, to łatwo jest ulec sugestii, że trudności powstające podczas przyspieszania cząstek do coraz większych prędkości powstają z powodu wzrostu masy cząstek.

Bogdan Szenkaryk "Pinopa"

Polska, Legnica, 22.11.2014.