pytanie:

Czy odcinek mający dwa końce o nazwie krzywa Hilberta wypełniający kwadrat o boku 1, jest dłuższy od prostej nie mającej końców o nazwie oś liczbowa?

Odpowiedź:

TAK

Dowód:

Tu miałem wyprowadzić dowód, ale nie zrobię tego, bo wyjeżdżam na urlop i do końca lipca mnie nie będzie. Dowód jest prosty, intuicyjny i każdy kto zna matematykę® potrafi go samodzielnie, bez wysiłku wyprowadzić - wystarczy podzielić kwadrat na odpowiednią ilość kwadracików elementarnych i połączyć ich środki za pomocą linii ciągłej nieprzecinającej się, przy czym niespodzianką dla badaczy będzie gdy zauważą, że im mniejsze kwadraciki to tym dłuższy ten nieskończony odcinek.

Edward Robak* z Nowej Huty ۞ Technik Elektronik :)

Krzywa Peano

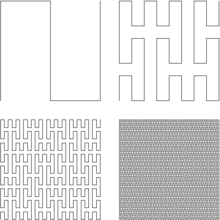
Kolejne etapy powstawania krzywej Peano

Krzywa Peano – przykład ciągłego odwzorowaniaodcinka na kwadrat.

Gdy w roku 1887 Camille Jordan podał następującą definicję krzywej (nazywanej dzisiaj krzywą Jordana):

krzywa jest to funkcja ciągła określona na odcinku [0,1]

wydawało się, że jest to definicja nieźle oddająca intuicję matematyków. Krzywa w tym rozumieniu nie jest co prawda "linią", lecz funkcją, ale "udziwnienie" jest pozorne, bo obraz odcinka [0,1] poprzez tę funkcję w "wielu naturalnych" przypadkach jest właśnie tym, co chcielibyśmy linią nazwać.

Jednak trzy lata później, w roku 1890, włoski matematyk Giuseppe Peano podał przykład krzywej w sensie Jordana, który kłócił się z naturalną intuicją – okazało się bowiem, że ciągłym obrazem odcinka może być cały kwadrat.

Niezależnie od Peano podobną krzywą rozpatrywał i skonstruował w tym samym czasie David Hilbert.

https://pl.wikipedia.org/wiki/Krzywa_Peano

Krzywa Hilberta[edytuj]

Krzywa Hilberta – przykład krzywej, która wypełnia całkowicie płaszczyznę, tzn. przechodzi przez wszystkie punkty płaszczyzny. Konstrukcja tej krzywej została podana przez Davida Hilberta.

Pierwsze sześć przybliżeń krzywej Hilberta

https://pl.wikipedia.org/wiki/Krzywa_Hilberta

Hn is the nth approximation to the limiting curve. The Euclidean length of Hn is $\textstyle 2^n - {1 \over 2^n}$ , i.e., it grows exponentially with n, while at the same time always being bounded by a square with a finite area. https://en.wikipedia.org/wiki/Hilbert_curve