Jakiś czas temu zderzyłem się z takim problemem, jak wyliczyć (zaprogramować) wektor prędkości kątowej Ω dla danej chwili, mając jedynie wektory położenia r i prędkości v dla punktów bryły sztywnej. Podczas obrotu BS wektor Ω rzadko kiedy jest stały w czasie, zarówno w układzie inercjalnym jak i nieinercjalnym układzie BS, pokazują to moje symulacje.
https://youtu.be/e0V8Ce8wyyI
https://youtu.be/CAVXGDMbquk
Mając wartość energii obrotu i wektor krętu można wyliczyć trajektorię po której porusza się końcówka wektora Ω. Aby zaprogramować konkretny obrót wystarczy w sumie jedynie pozycja Ω_ względem zdefiniowanej BS i na podstawie tego można dość łatwo wyliczyć wszystkie wektory. Ale jak wyliczyć w konkretnej chwili Ω_ dla całej bryły kiedy jej nie mamy?
Po długiej analizie zagadnienia rozwiązanie okazało się nieoczekiwanie proste. Postanowiłem wyliczyć jednostkowe prędkości kątowe dla osi głównych i, j, k i po ich sumowaniu wychodził mi wektor Ω. Wtedy liczyłem na liczbach i mi wychodziło ale brałem r=1 i Ω=1 i to w dwóch wymiarach, teraz okazuje się że jeden szczegół mi umkną ale dowodząc prawdziwości tego założenia go znalazłem.
Tak jak w poprzedniej notce wektory będą opisane ze znakiem"_", czyli wektor r_, a moduł to r=|r_|
Przedstawmy więc BS jako sześć punktów po dwa symetryczne na każdej osi.
mi1(rix, 0, 0); mi2(-rix, 0, 0)
mj1(0, rjy, 0); mj2(0, -rjy, 0)
mk1(0, 0, rkz); mk2(0, 0, rkz)
gdzie i,j,k są osiami do siebie prostopadłymi
Każda BS ma swoje trzy główne momenty bezwładności, mając teraz ten model możemy tak dobrać masy punktów m aby taki model odwzorowywał zachowywanie się każdej dowolnej BS. Do wyznaczaniu prędkości masa jest nieistotna, dlatego wyznaczanie masy punktów m jest nam teraz nie potrzebne.
Własność wektora Ω dla bryły sztywnej jest taka, że wektor prędkości każdego punktu spełnia równanie
v_ = Ω_ x r_
Nie ma ty znaczenia kąt nachylenia wektorów Ω_ i r_, rachunek iloczynu wektorowego wyznacza prawidłowe v_
Nasze Ω to
Ω ( Ωx, Ωy, Ωz)
Na każdej osi głównej mamy dwa symetryczne względem środka ciężkości punkty więc wystarczy że policzymy v dla trzech punktów naszej BS mi1, mj1, i mk1
v1_(0, Ωzrix, -Ωyrix) dla mi1
v2_(-Ωzrjy, 0, Ωxrjy) dla mj1
v3_(Ωyrkz, -Ωxrkz, 0) dla mk1
v1_ nie jest wektorem na osi i a wektorem prędkości dla punktu mi1.
Nowi czytelnicy muszą się zaznajomić z moją poprzednią notką, gdzie przeprowadziłem dowód na poprawność algorytmu odwracania iloczynu wektorowego z użyciem odwrotności wektora. Stali czytelnicy zapewne znają już tą technikę
https://www.salon24.pl/u/przestrz/870642,odwrotnosc-iloczynu-wektorowego-i-wzory-opisujace-ruch-obrotowy
Wzór na prędkość kątową to
ω_ = 1/r_ x v_
1/r_ (rx/r2, ry/r2, rz/r2)
r = √( rx2+ry2+rz2)
czyli dla naszych punktów
1/ri_ (rix/rix2, 0, 0)
1/rj_ (0, rjy/rjy2, 0)
1/rk_ (0, 0, rkz/rkz2)
moduły z wektorów położenia to
|ri_| = √(rix)2 = ri
|rj_| = √(rjy)2 = rj
|rk_| = √(rkz)2 = rk
Wzory na ω
ω1_ = 1/ri_ x v1_
ω2_ = 1/rj_ x v2_
ω3_ = 1/rk_ x v3_
ω1_ = (0, Ωy, Ωz)
ω2_ = (Ωx, 0, Ωz)
ω3_ = (Ωx, Ωy, 0)
sumujemy wektory
Ω`_ = ω1_ + ω2_ + ω3_
Ω`_ = 2Ω_
Czyli
Ω= (ω1_ + ω2_ + ω3_ )/2
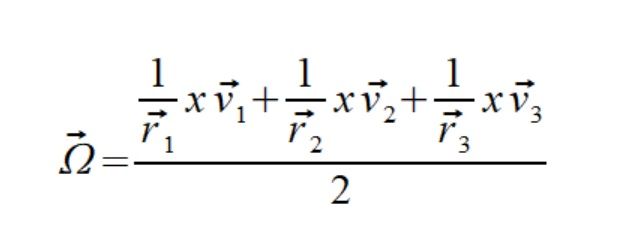
Mamy więc bardzo przyjemny sposób na wyliczenie chwilowej prędkości kątowej która znajduje się na chwilowej osi obrotu.
Po raz kolejny pełny sukces. Znając te wzory oraz odwrotność iloczynu wektorowego oraz kilka innych podstawowych wzorów z dynamiki, wyliczanie większość wektorów dla każdego punktu staje się proste, łatwe i przyjemne.
Niedawno udowadniałem istnienie wewnętrznego moment sił, który jest odpowiedzialny za charakterystyczne dla tego ruchu zmiany wektora prędkości kątowej w czasie.
https://www.salon24.pl/u/przestrz/833687,wyprowadzenie-rownania-momentu-sily-wewnetrznych
Wyszło nam że ten moment siły ujemnie proporcjonalny do prędkości kątowej i zmiany momentu bezwładności w czasie.
M=-ω(dI/dt)
Czyli mamy przyczynę tego momentu siły ale nasuwa się następne pytanie: Dlaczego podczas swobodnie obracającej się BS z różnymi głównymi momentami bezwładności, dochodzi do samoistnej zmiany momentu bezwładności w czasie? Co jest tego przyczyną i dlaczego tak się dzieje?
Kolejna odpowiedź generuje kolejne pytanie, ale miejmy nadzieje ta odpowiedź będzie już ostatnią, po której otworzy nam się kompletny widok na każdy szczegół tego fascynującego i bardzo intrygującego ruchu.
Inne tematy w dziale Technologie

