Odwrotność iloczynu wektorowego i wzory opisujące ruch obrotowy.

    Nieoczekiwana awaria samochodu uziemiła mnie w domu. Moje dotychczasowe rozważania były nieustannym parciem do przodu, nie przywiązywałem zbytniej uwagi do estetyki i precyzji przekazu, przez co moje notki są dość chaotyczne i trudne do zrozumienia. Ponieważ miałem dość długą przerwę wypadłem z rytmu i też sporo się pozapominało. Najwyższy czas trochę się cofnąć do tył i uporządkować zagadnienia które już udało się zrozumieć i znaleźć na nie odpowiedzi. Trzeba przeprowadzić jakieś dowody na poprawność tych założeń.

    Przy opisie mechaniki obrotu BS bardzo przydatny jest iloczyn wektorowy, który pozwala na wyliczenie takich pseudo wektorów jak prędkość kątowa, czy moment siły czy wiele innych przydatnych wektorów

https://pl.wikipedia.org/wiki/Iloczyn_wektorowy

Ponieważ nie wiem jak używać na salonie24 czcionki do opisu wektorów, dlatego wektor będę oznaczał ze znakiem "_"

A_ -wektor A

A -skalar wektora A_

Iloczyn wektorowy dwóch wektorów A i B określa się następująco

A_ x B_ = C_            (1)

B_ x A_ = -C_

    Jak widać kolejność zapisu ma znaczenie i wyznacza kierunek wektora C, który jest wynikiem iloczynu wektorowego wektorów A na B. Kierunek ten możemy wyznaczyć używając reguły prawej dłoni.

"gdzie C_  jest prostopadły zarówno do A_ i B_ tzn. C_ jest wektorem normalnym do płaszczyzny wyznaczonej przez AB. Długość wektora C jest równa polu powierzchni równoległoboku wyznaczonego przez wektory A i B"

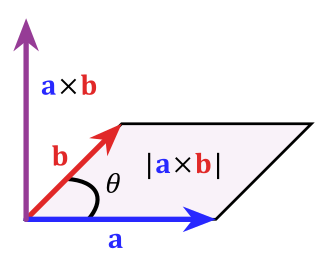
Iloczyn wektorowy w zapisie skalarnym przyjmuje postać

C=ABsinθ                    (2)

gdzie θ jest kątem pomiędzy wektorami A_ i B_

Dla kąta 90 stopni sinθ przyjmuje wartość 1. Przyjmując że wektor A_ leży na wersorze i, i jest prostopadły do wektora B_ który leży na wersorze j, to wektor C_ będący wynikiem iloczynu wektorowego leżeć będzie na wersorze k, który jest prostopadły zarówno do wersora i jak i wersora j. Wersory i,j,k tworzą trójwymiarowy układ współrzędnych.

Dla wersorów jednostkowych i=1, j=1, k=1 spełniają równości

i x j = k                    (3)

j x i = -k

j x k = i

k x j = -i

k x i = j

i x k = -j

Dla wektorów A_(ai,aj,ak), B_(bi,bj,bk) wynikiem iloczynu wektorowego jest

A_ x B_ = (ajbk-akbj, akbi-aibk, aibj-ajbi) = C_

Dla wektorów Ai_(ai,0,0) , Bj_(0,bj,0)

Ai_ x Bj_ = AiBj*k = Ck_                        (4)

Ważne! Próba odwrócenia operacji jest poprawna tylko w szczególnych przypadkach. Używając  (4)

Ai_ x Bj_ = AB*k = Ck_
wersor jest równy 1 więc
Ck_ x Ai_ = CA*j = (AB)A*j = Dj_                         (5)
Dj_=A²B*j                                       
jeżeli A=1 to Bj_=Dj_
jeżeli A≠1 to Bj_≠Dj_ , wektory Dj_ i Bj_ leżą na tej samej prostej mają ten sam kierunek ale mają inne długości.

Analogicznie druga sytuacja

Ai_ x Bj_ = AB*k = Ck_
wersor jest równy 1 więc
Bj_ x Ck_ = BC*i = B(AB)*i = Ei_                        (6)
Ei_=AB²*j                                       

jeżeli B=1 to Ai_=Ei_
jeżeli B≠1 to Ai_≠Ei_ , wektory Ai_ i Ei_ leżą na tej samej prostej, mają ten sam kierunek ale mają inne długości.

    Do dalszych rozważań musimy przyjąć że pracujemy na wektorach do siebie zawsze prostopadłych, jednak są sytuacje kiedy wektory nie są do siebie prostopadłe, wtedy poniższe rozwiązania będą dawały błędne wyniki i obowiązuje wzór (2). Dużo czasu poświęciłem aby móc odwrócić każdą operacje iloczynu wektorowego, ale obawiam się że bez ekstra zapisu kąta θ będzie to niemożliwe i w wyniku iloczynu wektorowego (w wektorze C_) informacja o tym kącie bezpowrotnie przepada.

    W opisie mechaniki obrotu Bryły sztywnej iloczyn wektorowy ma sporo zastosowań i sporo elementów jest opisana za jego pomocą. Weźmy teraz na przykład wektor krętu, jest on definiowany jako wynik iloczynu wektora położenia r na wektor pędu p, L_=r_xp_ . Tak jak pisałem przed chwilą zakładamy że wektory r_ i p_ są do siebie prostopadłe. Dość często miałem sytuacje gdzie w moich symulacjach musiałem wyliczyć operacje odwrotne, jak to w miarę sprytnie zrobić? Prawidłowa jest na przykład taka operacja

p_ = (L_ x r_)/r²                       (7)

Prawdę mówiąc miałem spory problem ze znalezieniem opisu jak takie równanie użyć w praktyce. Musiałem więc sam znaleźć rozwiązanie i okazało się one dość proste. Zapisując równanie (4) skalarnie otrzymujemy takie proporcje

AB=C                                (8)

A=C/B

B=C/A

Jednak w iloczynie wektorowym kolejność ma znaczenie. Używając wzorów (3) i proporcji (8) ustalamy prawidłową kolejność

A_ x B_ = C_                            (9)

1/B_ x C_ = A_

C_ x 1/A_ = B_

Jednak dalej nie wiemy jak policzyć 1/B_ lub bardziej prawidłowo odwrotność wektora B_^-1. Rozwiązaniem jest

IB_I = √(bx²+by²+bz²) = B

1/B * B = 1

1/IB_I * IB_I = (1/√(bx2+by2+bz2)) * √(bx2+by2+bz2) = 1            (11)

Odwrotność wektora to

1/B_=(bx/B², by/B², bz/B²)                                    (12)

B = IB_I

Aby sprawdzić poprawność w wywodzie (6) za Bj_ wstawiamy Bj^-1_

Ai_ x Bj_ = AB*k = Ck_
wersor jest równy 1
1/Bj_ x Ck_ = (1/B)(AB)*i = Ei_ = Ai_                      (13)

i druga sytuacja, sprawdzamy wywód (5)

Ai_ x Bj_ = AB*k = Ck_
wersor jest równy 1
Ck_ x 1/Ai_ = (AB)(1/A)*j = Dj_ = Bj_                          (14)

    O ile mamy do czynienia że wszystkie wektory iloczynu wektorowego są prostopadłe do siebie, używając równań (9) możemy w łatwy sposób odwracać operacje iloczynu wektorowego. 

    Wzory opisujące mechanikę obrotu BS

Moment pędu

L = r x p
p = L x 1/r
r = 1/p x L

prędkość kątowa

v = ω x r
ω = 1/r x v
r = v x 1/ω

przyspieszenie dośrodkowe

ad = ω x v
v = ad x 1/ω
ω = 1/v x ad

Moment siły

M = r x F
r = 1/F x M
F = M x 1/r

przyspieszenie kątowe

as = ɛ x r
ɛ = 1/r x as
r = as x 1/ɛ

    Mam nadzieje że coś nie pomyliłem ponieważ mam straszny bałagan w notatkach a dawno się tym nie zajmowałem. W razie czego będę robił korekty.