Wszystko jest kwestią względną. Patrząc na pozycje wektora krętu poniżej przedstawiony algorytm, można powiedzieć że jest skuteczny (wektor krętu zmienia pozycje o tysięczne części na 10 tyś kroków). Jedni powiedzą że to dużo drudzy że mało, ja osobiście będę dążył do znacznego zmniejszenia tego błędu, ale na dzień dzisiejszy jestem z takiego błędu zadowolony. Nie znam algorytmów które metodą krokową uzyskiwały by lepszą dokładność.
Co znaczy że algorytm jest skuteczny? Znaczy to że wynik uzyskany za jego pomocą pozwala odtworzyć z dość dobrą dokładnością zachowanie się mechaniki obrotu BS. Chcę tu zaznaczyć że skuteczny nie oznacza prawdziwy, to że wynik się zgadza nie oznacza że założenia są prawdziwe, to dopiero trzeba udowodnić.
Skąd wiem że moje symulacje odpowiadają rzeczywistości? Zakładam że wzory Eulera poprawnie opisują mechanikę obrotu BS i pierwsze symulacje były oparte na tych wzorach. Oczywiście moje symulacje nie zostały zweryfikowane przez profesjonalistów (nikt na poważnie się tym nie zainteresował), jednak wszelkie próby weryfikacji na podstawie ogólnie dostępnej wiedzy na ten temat wypadają pozytywnie. Nie znalazłem nic co by mogło sugerować że moje symulacje znacząco odbiegają od rzeczywistości. Wyniki nowych algorytmów na innych założeniach weryfikuje ze starymi i dopiero po uzyskaniu odpowiedniej dokładności przedstawiam nowe rozwiązania (często jest to eliminacja mnóstwa błędnych założeń).
Ostatnio przedstawiłem algorytm działający na podstawie momentu siły wyliczonego ze wzoru
M = L x ω (1)
Skąd ten wzór opisałem w poprzedniej notce
https://www.salon24.pl/u/przestrz/826080,uproszczony-algorytm-symulacji-obrotu-bs
Teraz trzeba pokazać skąd ten moment siły się bierze. Aby to zobaczy należy rozebrać wzór (1) na czynniki pierwsze.
Iɛ = Iω x ω (2a)
I(dω /dt) + ω x Iω = 0 (2b)
Na podstawie tego wzoru wyprowadzamy równania Eulera
Ixɛx = Iyωyωz – Izωzωy (3)
Iyɛy = Izωzωx – Ixωxωz
Izɛz = Ixωxωy – Iyωyωx
Trzeba pamiętać że pracujemy na idealistycznym modelu gdzie wcześniej wyznaczono główne momenty bezwładności i umieszczono je na osiach głównych. Masy zostały wyidealizowane do pojedynczych punktów po dwa na każdej osi głównej. Wygląda to mniej więcej tak.
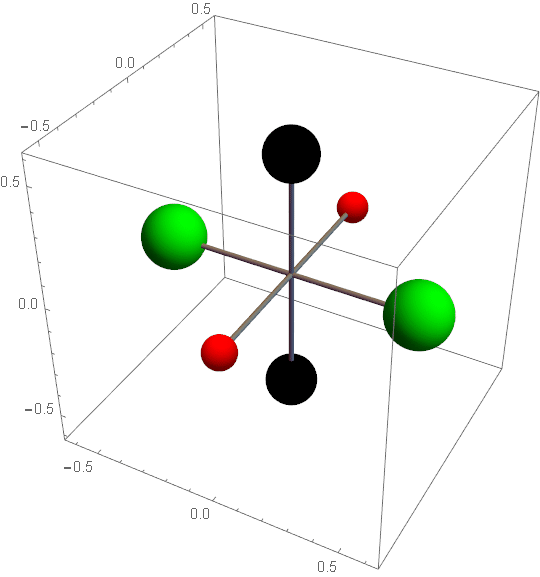
Teraz rozkładamy na czynniki pierwsze jeden z parametrów.
Ixωxωy=(mxr2x)ωxωy (4)
mx- masa na osi głównej x
rx- ramię masy mx
ωxy jest nachylona do ramienia rx pod pewnym kątem (rysunek poniżej), a więc
ωx=cos(a) (5)
ωy=sin(a)
Z równania (2a) wiemy że wyniku równania (4) otrzymujemy moment siły M. Pamiętając o równaniach (5) Zapiszmy równanie (4) następująco
Mx=(mxr2)ω2sin(a)cos(a) (7a)
Zauważmy że moment siły (7a) zeruje się gdy wektor ω jest równoległy z wektorem r, sin0°=0 oraz gdy wektory te są do siebie prostopadłe cos90°=0.
Jak teraz uzyskać ten moment siły? Zaleca się by we wzorach Eulera główne momenty bezwładności pokrywały się osiami głównymi. W takim układzie odniesienia mamy
Mx=(mxr2)ωxωy (7b)
Jednak w układzie odniesienia gdzie wektor ω znajduje się na jednej z osi głównych wzór będzie wyglądał na przykład tak
Mx=(mxω2)rxry (7c)
Podobny układ rozpatrywałem już wcześniej
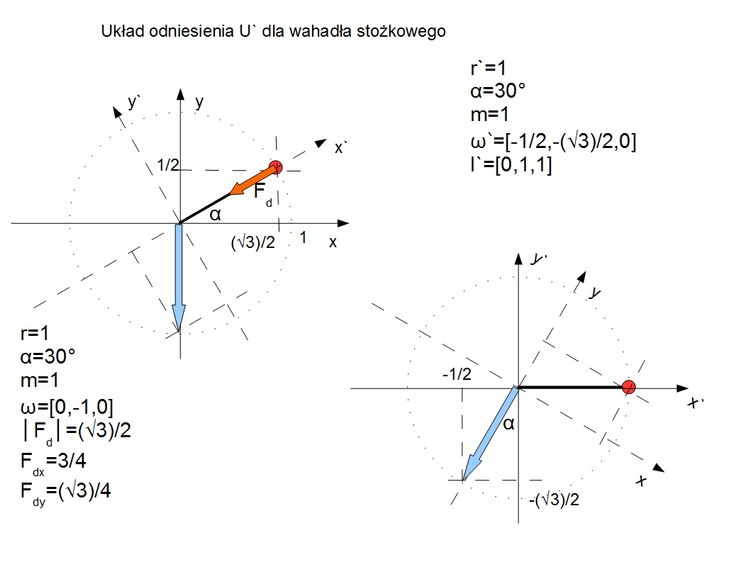
trochę więcej, chociaż zapewne nieprecyzyjnie i chaotycznie pisałem o tym wcześniej.
https://www.salon24.pl/u/przestrz/771163,mechanika-obrotu-punktu-bryly-sztywnej
Przypomnijmy teraz wzór na siłę dośrodkową
Fd=-mrω2 (8)
Gdzie r jest wektorem położenia prostopadły do osi obrotu. Bierzemy teraz model wahadła stożkowego.
https://pl.wikipedia.org/wiki/Wahad%C5%82o_sto%C5%BCkowe
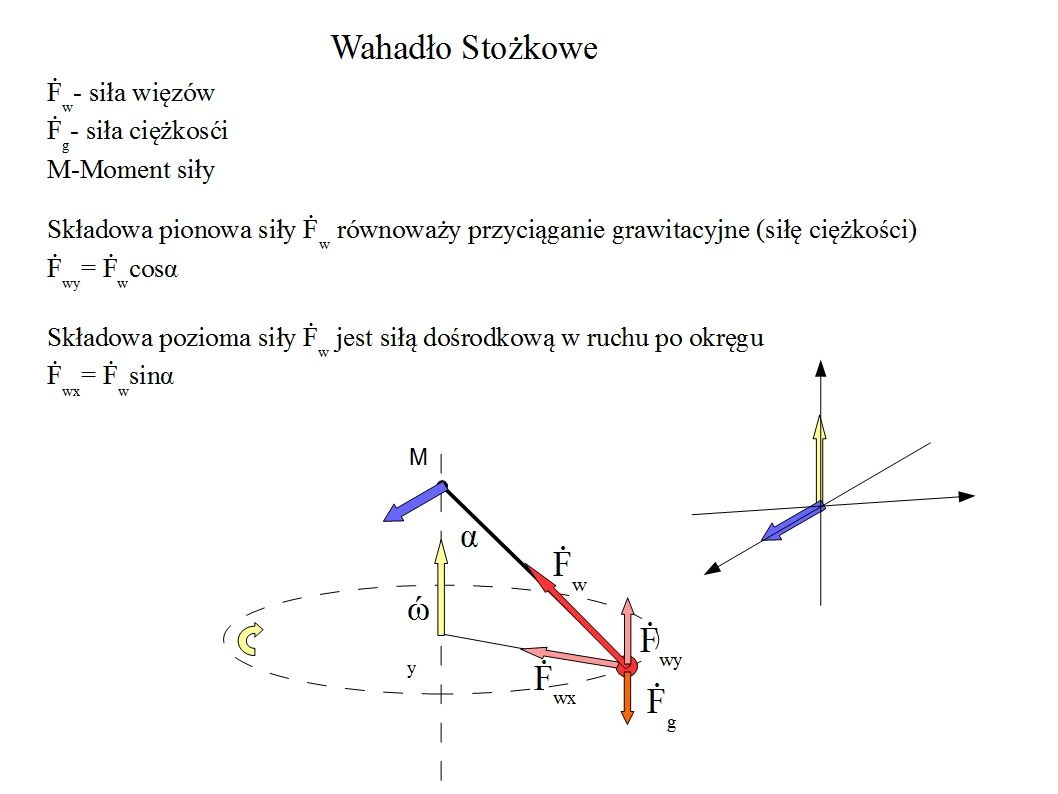
Ponieważ do wzoru (8) potrzebujemy r prostopadłe do wektora ω ustalamy zależność
r┴=rsin(a) (9)
Jak widzimy siła więzów jest to
Fw=-mω2 *rsin(a) (10)
Składowa pionowa Fw unosząca masę w wahadle stożkowym, która to jest równoległa do wektora ω to:
Fwp=Fwcos(a) (11)
Fwp tworzy moment siły który wyliczamy z iloczynu wektorowego
M = r x F (12)
Podstawiając teraz (10) do (11) a następnie korzystając ze wzoru (12) otrzymujemy wzór (7a). W ten sposób mamy szczegóły równań Eulera (3) oraz przyczynę sumarycznego momentu siły ze wzoru (1). Nie ma niespodzianek sprawdzałem to już wcześniej ze skutkiem pozytywnym.
https://www.salon24.pl/u/przestrz/812610,momenty-sil-w-mechanice-bs-pierwsza-proba-pozytywnie
Problem polega na interpretacji wzoru na silę dośrodkową (8). Niestety nie doczytałem się jednoznacznej odpowiedzi jaki ten wektor ma kierunek. Z jednej strony są podręczniki które twierdzą że siła ta musi być siłą centralną, gdyż tylko wtedy wypadkowa sił będzie równa zero, z drugiej strony podręczniki opisują wahadło stożkowe, twierdząc że jest to siła do-osiowa jednak w takiej interpretacji skutkowało by to powstaniem jawnego Momentu sił. W takiej interpretacji wypadkowa sił się nie zeruje, pokazuje to ten schemat.
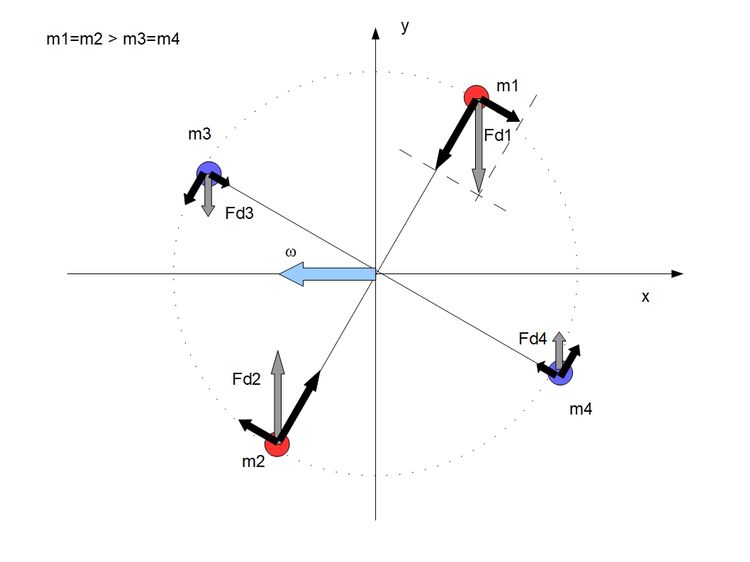
Większość komentatorów mojego bloga twierdzi że siły te muszą być do-osiowe, ale nie są oni konsekwentni w swoim stwierdzeniu, gdyż nie przeszkadza im to twierdzić że mimo że są to siły do-osiowe to i tak wypadkowa sił równa się zero. Niestety żaden z nich nigdy nie zadał sobie trudu by to sprawdzić i nie widzą oni że przeczą sami sobie. Niestety podobna sytuacja jest z momentem sił, twierdzą oni że M=Iɛ jest prawdziwe ale tak naprawdę w tych wzorach M=Iɛ jest fałszywe. Niestety nie umiem się z nikim dogadać gdyż nikt nie trzyma się konsekwentnie swoich stwierdzeń i przeczą sami sobie. Nikt z nich nie chce się przyznać do pomyłki i uparcie twierdzą że 2=3 jest prawdziwe. Choćbyście powtarzali tysiąckroć że siły więzów są do-osiowe i jednocześnie wypadkowa tych sił równa się zero i nie daje żadnego momentu sił, to i tak stwierdzenie takie jest fałszywe i nie zmienicie tego siła waszej woli. Mylić się jest rzeczą ludzką ale ten kto tkwi uparcie w błędzie jest głupcem. Jeżeli macie racje (jest taka możliwość) to należy poprawić podręczniki które twierdza że jest to siła centralna, a jeżeli podręczniki mają racje ma to też pewne konsekwencje które również Fizyką się nie spodobają.
Ponieważ równania (7) można uzyskać na kilka sposobów a nie wiem jeszcze który jest prawdziwy, na pierwszy ogień wybrałem interpretacje z do-osiowymi siłami więzów, ponieważ taki model był dla mnie najłatwiejszy do napisania.
Poniżej skuteczny algorytm, ale nie jestem przekonany czy prawdziwy, przypuszczam że będę umiał napisać co najmniej jeszcze jeden algorytm oparty na interpretacji o centralnych siłach więzów. Pytanie jest który jest prawdziwy i jak to sprawdzić? Być może uda mi się to zrobić przy pomocy wektora krętu, ale jeżeli również ta próba nie udowodni błędności którejś z interpretacji, pozostanie już chyba tylko weryfikacja eksperymentalna.
from visual import *
m1=1 #masy na osiach 1-x, 2-y, 3-z
m2=0.5
m3=0
rx=1 #dlugosc ramion
ry=1
rz=1
wx=0. #omega startow
wy=1.
wz=0.1
W=vector(wx,wy,wz)
Ix=(m2*ry*ry)+(m3*rz*rz) #moment bezwaladnosci
Iy=(m1*rx*rx)+(m3*rz*rz)
Iz=(m2*ry*ry)+(m1*rx*rx)
L=vector((W.x*Ix),(W.y*Iy),(W.z*Iz)) #L=WI
print "L0",mag(L),L
bryla=frame() #definowanie BS
masa11=sphere(frame=bryla, pos = vector(rx,0,0), radius =0.02, color = color.red)
masa12=sphere(frame=bryla, pos = vector(-rx,0,0), radius =0.02, color = color.red)
masa21=sphere(frame=bryla, pos = vector(0,ry,0), radius =0.02, color = color.blue)
masa22=sphere(frame=bryla, pos = vector(0,-ry,0), radius =0.02, color = color.blue)
masa31=sphere(frame=bryla, pos = vector(0,0,rz), radius =0.02, color = color.green)
ramiex=cylinder(frame=bryla, pos = masa11.pos, radius =0.005, axis=masa12.pos-masa11.pos)
ramiey=cylinder(frame=bryla, pos = masa21.pos, radius =0.005, axis=masa22.pos-masa21.pos)
oX=arrow(axis=vector(1,0,0), shaftwidth=0.01, color =vector(0.7,0.9,0.5)) #osie ukladu inercjalnego
oY=arrow(axis=vector(0,1,0), shaftwidth=0.01, color =vector(0.7,0.9,0.5))
oZ=arrow(axis=vector(0,0,1), shaftwidth=0.01, color =vector(0.7,0.9,0.5))
#kropkaw=sphere(pos=vector(W.x,W.y,W.z), radius=0.01, color= color.blue, make_trail=True)
omega=arrow(axis=vector(W.x,W.y,W.z), color= color.blue, shaftwidth=0.01)
#epsilon=arrow(axis=vector(0,0,0), color= color.green, shaftwidth=0.01)
#momentsi=arrow(axis=vector(0,0,0), shaftwidth=0.01)
os=cylinder(axis=-vector(W.x,W.y,W.z), radius=0.005)
kret=arrow(axis=vector(L.x,L.y,L.z), color= color.red, shaftwidth=0.01)
predkos1=arrow(pos=vector(1,0,0), axis=vector(0,0,0.01), color= color.yellow, shaftwidth=0.01)
predkos2=arrow(pos=vector(0,1,0), axis=vector(0,0,0.01), color= color.yellow, shaftwidth=0.01)
predkos3=arrow(pos=-vector(1,0,0), axis=-vector(0,0,0.01), color= color.yellow, shaftwidth=0.01)
predkos4=arrow(pos=-vector(0,1,0), axis=-vector(0,0,0.01), color= color.yellow, shaftwidth=0.01)
#sila wiezow
sila1=arrow(pos=vector(1,0,0), axis=vector(0,0.1,0), color= vector(0.,0.8,0.8), shaftwidth=0.02)
sila2=arrow(pos=vector(0,1,0), axis=vector(0.1,0,0), color= vector(0.,0.8,0.8), shaftwidth=0.02)
sila3=arrow(pos=-vector(1,0,0), axis=-vector(0,0.1,0), color= vector(0.,0.8,0.8), shaftwidth=0.02)
sila4=arrow(pos=-vector(0,1,0), axis=-vector(0.1,0,0), color= vector(0.,0.8,0.8), shaftwidth=0.02)
#skladowa dosrodkowa sily wiezow
sila1d=arrow(pos=vector(1,0,0), axis=vector(0,0.1,0), color= vector(0.4,0.2,0.8), shaftwidth=0.02)
sila2d=arrow(pos=vector(0,1,0), axis=vector(0.1,0,0), color= vector(0.4,0.2,0.8), shaftwidth=0.02)
sila3d=arrow(pos=-vector(1,0,0), axis=-vector(0,0.1,0), color= vector(0.4,0.2,0.8), shaftwidth=0.02)
sila4d=arrow(pos=-vector(0,1,0), axis=-vector(0.1,0,0), color= vector(0.4,0.2,0.8), shaftwidth=0.02)
#skladowa sily wiezow dajaca M
sila1p=arrow(pos=vector(1,0,0), axis=vector(0,0.1,0), color= vector(0.4,0.2,0.8), shaftwidth=0.02)
sila2p=arrow(pos=vector(0,1,0), axis=vector(0.1,0,0), color= vector(0.4,0.2,0.8), shaftwidth=0.02)
sila3p=arrow(pos=-vector(1,0,0), axis=-vector(0,0.1,0), color= vector(0.4,0.2,0.8), shaftwidth=0.02)
sila4p=arrow(pos=-vector(0,1,0), axis=-vector(0.1,0,0), color= vector(0.4,0.2,0.8), shaftwidth=0.02)
dt=0.001
t=0
n=0
while t<10000:<br /> rate(100)
r1=bryla.frame_to_world(masa11.pos) #pozycje mas
r2=bryla.frame_to_world(masa21.pos)
r3=bryla.frame_to_world(masa31.pos)
v1=vector((W.y*r1.z)-(W.z*r1.y),(W.z*r1.x)-(W.x*r1.z),(W.x*r1.y)-(W.y*r1.x)) #predkosci mas
v2=vector((W.y*r2.z)-(W.z*r2.y),(W.z*r2.x)-(W.x*r2.z),(W.x*r2.y)-(W.y*r2.x))
WW=mag(W) #dlugosc W
Wo=vector(W.x/(WW*WW),W.y/(WW*WW),W.z/(WW*WW)) #1/W odwrotnosc omegi
rxp=vector((v1.y*Wo.z)-(v1.z*Wo.y),(v1.z*Wo.x)-(v1.x*Wo.z),(v1.x*Wo.y)-(v1.y*Wo.x)) # wektor doosiowy r = v x 1/w
ryp=vector((v2.y*Wo.z)-(v2.z*Wo.y),(v2.z*Wo.x)-(v2.x*Wo.z),(v2.x*Wo.y)-(v2.y*Wo.x))
a=diff_angle(W,r1) #katy miedzy r, W
b=diff_angle(W,r2)
F1=-(m1*WW*WW)*rxp #sila dosrodkowa Fx`=mrx`w^2 rx=r*sina
F2=-(m2*WW*WW)*ryp
Fxc=-vector(r1.x,r1.y,r1.z) #kierunek sily dosrodkowej
Fyc=-vector(r2.x,r2.y,r2.z)
Fxc.mag=mag(F1)*sin(a) #wartosc sily dosrodkowej
Fyc.mag=mag(F2)*sin(b)
Fxm=F1-Fxc #wektor sily dajacej M
Fym=F2-Fyc
#Momenty sil z osi x` i y`
Mx=vector((r1.y*Fxm.z)-(r1.z*Fxm.y),(r1.z*Fxm.x)-(r1.x*Fxm.z),(r1.x*Fxm.y)-(r1.y*Fxm.x))
My=vector((r2.y*Fym.z)-(r2.z*Fym.y),(r2.z*Fym.x)-(r2.x*Fym.z),(r2.x*Fym.y)-(r2.y*Fym.x))
MM=Mx+My
predkos1.pos=vector(r1.x,r1.y,r1.z)
predkos1.axis=vector(v1.x,v1.y,v1.z)/3
predkos2.pos=vector(r2.x,r2.y,r2.z)
predkos2.axis=vector(v2.x,v2.y,v2.z)/3
predkos3.pos=-vector(r1.x,r1.y,r1.z)
predkos3.axis=-vector(v1.x,v1.y,v1.z)/3
predkos4.pos=-vector(r2.x,r2.y,r2.z)
predkos4.axis=-vector(v2.x,v2.y,v2.z)/3
sila1.pos=vector(r1.x,r1.y,r1.z)
sila1.axis=vector(F1.x,F1.y,F1.z)
sila2.pos=vector(r2.x,r2.y,r2.z)
sila2.axis=vector(F2.x,F2.y,F2.z)
sila3.pos=-vector(r1.x,r1.y,r1.z)
sila3.axis=-vector(F1.x,F1.y,F1.z)
sila4.pos=-vector(r2.x,r2.y,r2.z)
sila4.axis=-vector(F2.x,F2.y,F2.z)
sila1d.pos=vector(r1.x,r1.y,r1.z)
sila1d.axis=vector(Fxc.x,Fxc.y,Fxc.z)
sila2d.pos=vector(r2.x,r2.y,r2.z)
sila2d.axis=vector(Fyc.x,Fyc.y,Fyc.z)
sila3d.pos=-vector(r1.x,r1.y,r1.z)
sila3d.axis=-vector(Fxc.x,Fxc.y,Fxc.z)
sila4d.pos=-vector(r2.x,r2.y,r2.z)
sila4d.axis=-vector(Fyc.x,Fyc.y,Fyc.z)
sila1p.pos=vector(r1.x,r1.y,r1.z)
sila1p.axis=vector(Fxm.x,Fxm.y,Fxm.z)
sila2p.pos=vector(r2.x,r2.y,r2.z)
sila2p.axis=vector(Fym.x,Fym.y,Fym.z)
sila3p.pos=-vector(r1.x,r1.y,r1.z)
sila3p.axis=-vector(Fxm.x,Fxm.y,Fxm.z)
sila4p.pos=-vector(r2.x,r2.y,r2.z)
sila4p.axis=-vector(Fym.x,Fym.y,Fym.z)
#tensor momentu bezwladnosci
TIxx=(m1*((r1.y*r1.y)+(r1.z*r1.z)))+(m2*((r2.y*r2.y)+(r2.z*r2.z)))
TIyy=(m1*((r1.x*r1.x)+(r1.z*r1.z)))+(m2*((r2.x*r2.x)+(r2.z*r2.z)))
TIzz=(m1*((r1.x*r1.x)+(r1.y*r1.y)))+(m2*((r2.x*r2.x)+(r2.y*r2.y)))
TIxy=-(m1*r1.x*r1.y)-(m2*r2.x*r2.y)
TIxz=-(m1*r1.x*r1.z)-(m2*r2.x*r2.z)
TIyx=-(m1*r1.y*r1.x)-(m2*r2.y*r2.x)
TIyz=-(m1*r1.y*r1.z)-(m2*r2.y*r2.z)
TIzx=-(m1*r1.z*r1.x)-(m2*r2.z*r2.x)
TIzy=-(m1*r1.z*r1.y)-(m2*r2.z*r2.y)
#wyznacznik macierzy
A=(TIxx*TIyy*TIzz)+(TIxy*TIyz*TIzx)+(TIxz*TIyx*TIzy)-(TIxx*TIzy*TIyz)-(TIyy*TIzx*TIxz)-(TIzz*TIyx*TIxy)
#I^-1
OTIxx=((TIyy*TIzz)-(TIyz*TIzy))/A
OTIyy=((TIxx*TIzz)-(TIxz*TIzx))/A
OTIzz=((TIxx*TIyy)-(TIxy*TIyx))/A
OTIxy=((TIxz*TIzy)-(TIxy*TIzz))/A
OTIxz=((TIxy*TIyz)-(TIxz*TIyy))/A
OTIyx=((TIyz*TIzx)-(TIyx*TIzz))/A
OTIyz=((TIxz*TIyx)-(TIyz*TIxx))/A
OTIzx=((TIyx*TIzy)-(TIzx*TIyy))/A
OTIzy=((TIxy*TIzx)-(TIzy*TIxx))/A
#L=vector((W.x*TIxx+W.y*TIxy+W.z*TIxz),(W.x*TIyx+W.y*TIyy+W.z*TIyz),(W.x*TIzx+W.y*TIzy+W.z*TIzz))
#print t, "L", mag(L),L
#M=vector((L.y*W.z)-(L.z*W.y),(L.z*W.x)-(L.x*W.z),(L.x*W.y)-(L.y*W.x)) #M=Lxw
#print t, M+MM
M=-vector(MM.x,MM.y,MM.z)
if n<1000:<br /> n=n+1
else:
LL=vector((W.x*TIxx+W.y*TIxy+W.z*TIxz),(W.x*TIyx+W.y*TIyy+W.z*TIyz),(W.x*TIzx+W.y*TIzy+W.z*TIzz))
print t,mag(LL),LL
n=1
E=vector((M.x*OTIxx+M.y*OTIxy+M.z*OTIxz),(M.x*OTIyx+M.y*OTIyy+M.z*OTIyz),(M.x*OTIzx+M.y*OTIzy+M.z*OTIzz)) #e=M*I^-1
E=E.rotate(angle=mag(W)*dt,axis=W)
bryla.rotate (angle=mag(W)*dt,axis=W)
W.x=W.x+E.x*dt #wspolrzedne omegi
W.y=W.y+E.y*dt
W.z=W.z+E.z*dt
omega.axis=vector(W.x,W.y,W.z)
os.axis=-vector(W.x,W.y,W.z)
# epsilon.axis=vector(E.x,E.y,E.z)
# momentsi.axis=vector(M.x,M.y,M.z)
kret.axis=vector(L.x,L.y,L.z)
t=t+1
L=vector((W.x*TIxx+W.y*TIxy+W.z*TIxz),(W.x*TIyx+W.y*TIyy+W.z*TIyz),(W.x*TIzx+W.y*TIzy+W.z*TIzz))
print mag(L),L
Inne tematy w dziale Technologie

