Co ma omega do krętu? A miało być tak pięknie.

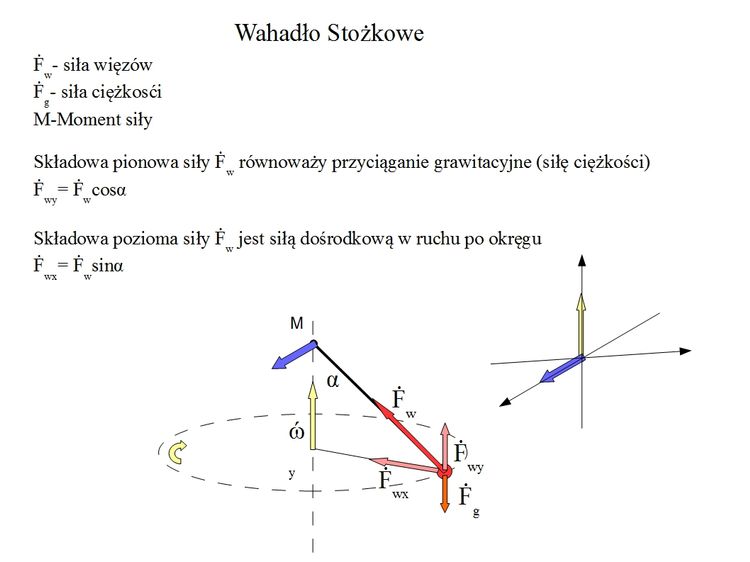
Przypomnę moje wahadło stożkowe i dwie składowe siły więzów
Fwd – składowa pozioma siła dośrodkowa do omegi i
Fwp – składowa pionowa siła równoległa do omegi dająca moment siły.

Znalazłem wzory na dv/dt i dω/dt i idealnie pasują one do mojej wizji.
dv/dt = d(ω x r)/dt = dω/dt x r + ω x dr/dt = ɛ x r + ω x v = M/I x r + ω x (ω x r)
dv/dt = ((r x F)/I) x r + ω x (ω x r)

Tak jak przypuszczam dv/dt ma dwie przyczyny:
((r x F)/I) x r najprawdopodobniej jest przyspieszeniem stycznym wywołane moją składowa pionową siły więzów Fwp.
A człon ω x (ω x r) jest to przyspieszenie dośrodkowe wywołane Fwd.
Więcej wyjaśni niezawodna profesor Popko

        Nie ma na to jeszcze dowodów ale taki stan rzeczy napawa mnie optymizmem i to mimo tego że ostatnio nasiliła się krytyka sensowności moich poszukiwań. Jak do tej pory moje pomysły były poddawane bardzo ostrej krytyce jednak oparte na intuicyjnych sformułowaniach, ja nie umiem ocenić prawdziwości tych argumentów dlatego tez wciąż poszukuje dowodu poprawności lub błędu moich założeń. Jak na razie im głębiej w las tym więcej argumentów że idę w dobrym kierunku. Wzory przedstawione dzisiaj są kolejnym elementem które na razie szacunkowo ale są zgodne z moimi założeniami.
        Wzór na dω/dt jest podobny.
dω/dt = d(r x v)/dt = dr/dt x v + r x dv/dt
ɛ = v x v + r x a

Co do tych wzorów to muszę jeszcze w nich pogrzebać aby wydobyć to co mi jest potrzebne.
        Wydawało mi się że już jestem prawie na mecie. Wystarczy jedynie policzyć przyspieszenia dośrodkowe i styczne dla jednego ramienia, udowodnić że moje siły Fwd i Fwp są przyczynami tych przyspieszeń a następnie zsumować wektory obiektów na trzech osiach głównych. Miało być tak pięknie a tu kolejna zapora.

       Na poprzednim blogu pokazałem następujący schemat rozkładu wektorów dla jednego ramienia.

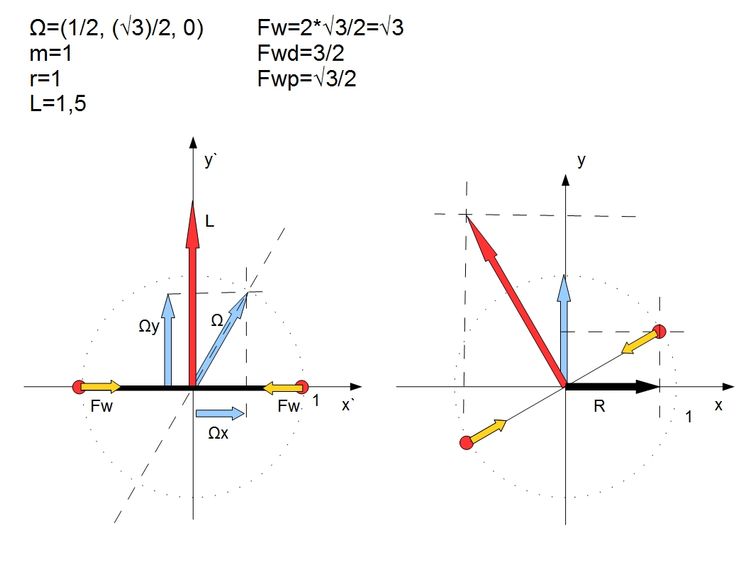
Na jednej z dyskusji zapytano mnie czy wiem że kiedy ramie nie będzie sztywne, to masy te nie będą się kręcić w ten sposób jak jest to na schemacie. Intuicyjna teza ta wydaje się logiczna ale od razu powstaje pytanie czym się różni sztywne ramie od naprężonego sznurka?

No i okazało że schemat jest błędny. Dlaczego? Wszystko przez chwilowe osie obrotu. Wyznacza się je biorąc dwa punkty i łącząc je prostą a następnie łączymy prostą końce wektorów prędkości. Przecięcie tych dwóch prostych daje nam chwilowy punkt obrotu.

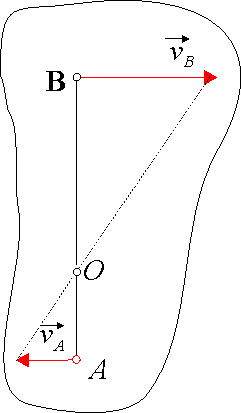
więcej źródło

http://home.agh.edu.pl/~wslosar/18.htm

Kiedy będziemy mieli dwa różne chwilowe punkty obrotu, prosta przechodząca przez nie tworzy oś obrotu. Okazuje się że dla mojego schematu oś obrotu zawsze jest równoległa z osią krętu. Znaczy to że jeżeli mamy bryłę sztywną złożoną z punktów materialnych leżących na jednej linii, to w czasie obrotu takiej bryły wektor omegi i krętu zawsze będą równoległe.

Teraz muszę lepiej zrozumieć jak z wektorów v tworzyć ω i zdefiniować jak ω jest nachylona do L. Być może stworze omegę w sposób sztuczny dla jednego punktu ale za nim to zrobię muszę mieć pewność że będzie to poprawne. Być może wymyślę coś innego

Ciekawostka moment bezwładności to mr^2 gdzie r jest promieniem prostopadłym do osi obrotu. Teraz z tym samym wektorem pędu na tym samym ramieniu, możemy mieć inny moment bezwładności kiedy ramie będzie swobodne a inne I kiedy ramie będzie sztywno połączone z innym ramieniem. Skąd masa na ramieniu wie jaki posiada moment bezwładności?

Kiedy wydaje mi się że już jestem blisko to wtedy powstaje nowy problem który w samotności muszę rozwiązać.