Zrozumieć mechanikę obrotu bryły sztywnej. Wektor prędkości, przyspieszenia i si

Aby zrozumieć dziwne zachowanie fikanie bryły sztywnej należy zrozumieć czym jest ruch, przyspieszenie i siła. Aby umieć kreatywnie używać wzorów dynamiki Newtona trzeba zrozumieć pewną filozofie która tkwi w tych prawach. Czyli trzeba nauczyć się stosować teorię w praktyce.

Wprowadzenie

Do tutejszych rozważań wystarczy uprościć obiekt materialny do punktu w przestrzeni gdzie znajduję się jego środek ciężkości. Potrzebny nam jest jeszcze jakiś hipotetyczny nieruchomy układ odniesienia.

Zacznijmy więc jeszcze raz od początku.

Jeżeli środek ciężkości nie zmienia swojego położenia względem układu odniesienia w czasie to mówimy że obiekt jest w stanie spoczynku. Jego wektor położenia względem układu się nie zmienia.

Jednak stan spoczynku jest stanem rzadkim i najczęściej obiekty przemieszają się w przestrzeni. Ich wektor położenia jest zmienny w czasie. Odejmując od wektora położenia końcowego, wektor położenia początkowego otrzymujemy wektor przemieszczenia się w przestrzeni układu.

Znając jednostkę czasu jaki upłyną od przemieszczenia się obiektu z punktu A do punktu B można wyznaczyć wektor prędkości średniej. v=dx/dt czyli wektor prędkości średniej równy jest przebytej drodze w jednostce czasu. Jeżeli wektor prędkości przymocowany do poruszającego się punktu jest stały w kolejnych odcinkach czasu, znaczy to że obiekt porusza się ruchem jednostajnym.

Jeżeli wektor prędkości uległ zmianie znaczy to że na obiekt działała siła i obiekt uległ przyspieszeniu wprost proporcjonalnym do wektora działającej siły i odwrotnie proporcjonalnym do masy a=F/m.

Tylko tyle i aż tyle. W tym krótkim wprowadzeniu zawarta jest cała tajemnica ruchu wszystkich obiektów we wszechświecie, przynajmniej tak uważano przed erą Einsteina i Mechaniki kwantowej. Jednak za pomocą teorii Einsteina jak i QM nie można zrozumieć mechaniki obrotu bryły sztywnej. Pozostaje nam jedynie klasyczne podejście.

Filozofia przyczynowo skutkowa

Zastanówmy się więc czym są trzy zasady dynamiki Newtona opisujące ruch obiektów materialnych? Są to trzy przypadki pewnej filozofii uznającą przyczynowo skutkową strukturę działania wszechświata. Każdy skutek ma swoją przyczynę która może być jednocześnie przyczyną następnego skutku. Najpierw mamy przyczynę a następnie skutek. Tłumacząc zasady dynamiki Newtona można je napisać tak:

Pierwsza zasada – jeżeli nie ma przyczyny lub przyczyny się niwelują to nie ma skutku.

Druga zasada – konkretna przyczyna daje konkretny skutek.

Trzecia zasada – akcja równa jest reakcji, akcja powoduje równą sobie reakcje, Oddziałujące na siebie obiekty są nawzajem dla siebie przyczyną a skutki są identyczne dla wszystkich obiektów.

Czym więc jest zmiana wektora prędkości? Jest to skutek.

Co jest jego przyczyną? Przyczyną jest działanie siły.

Czym jest siła? Siła nie jest obiektem i nie można jej obserwować bezpośrednio. Jednak śladem po niej, skutkiem jej działania jest zmiana wektora prędkości. Obserwując więc skutek możemy opisać przyczynę opisując ją wirtualnym wektorem siły, który jest jedynie wirtualnym sposobem naszego rozumienia tego zjawiska.

W ten sposób ludzkość obserwując skutki zrozumiała przyczynę takich zjawisk jak siła grawitacji, siła elektromagnetyczna czy siła więzów przy prędkości kątowej.

Ruch obrotowy.

Z drugiej zasady dynamiki wynika że jeżeli na obiekt nie działa siła to porusza się on ruchem jednostajnym. Przypadkiem szczególnym jest ruch obrotowy. Na punkty materialne obiektu swobodnie obracającego się nie działa żadna zewnętrzna siła a mimo to wektor prędkości punktów jest zmienny w czasie. Przyczyną tego jest działanie siły więzów które trzymają punkty materialne razem i w bryle sztywnej nie pozwalają na przemieszczenie się punktów względem siebie. przyczyną orbitowania punktu materialnego wokół osi obrotu jest działanie siły skierowanej do osi.

Fikołek

No i tutaj kończą się możliwości współczesnej fizyki. Pozostaje jeszcze przypadek szczególny ruchu obrotowego obiektów z niesymetrycznym rozmieszczeniem mas, które ni stąd ni zowąd czasami zaczyna robić fikołka wbrew siłom jakie zostały dotychczas zdefiniowane. Jest zmiana ruchu której nie umiemy przypisać przyczyny czyli siły która ten ruch powoduje.

Ponieważ nie znamy przyczyny przyjrzyjmy się skutkowi.

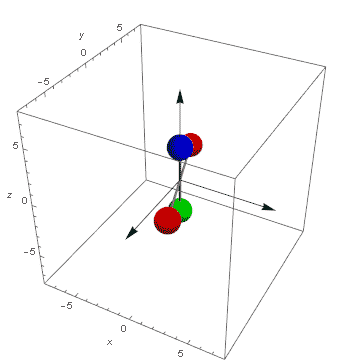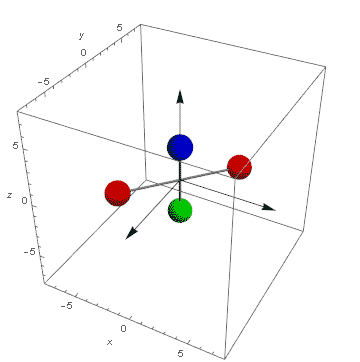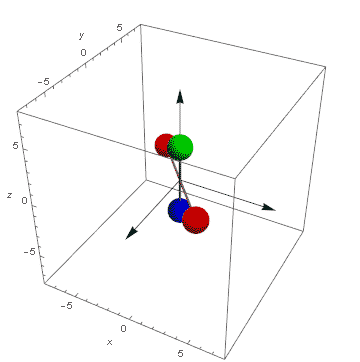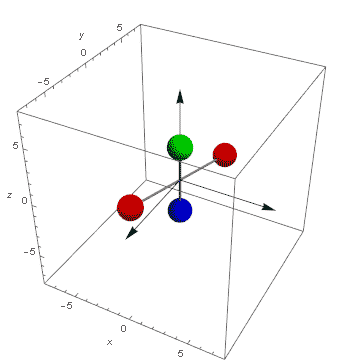
Przyjrzyjmy się jak zmieniają się wektory prędkości punktów znajdujących się na biegunie A, równiku C i pomiędzy nimi B. Celowo tutaj pominę bardzo ważny moment bezwładności. To on jest pośrednią przyczyną i odpowiada za tempo zmian, jednak rozpatrywanie go tutaj powoduje pewne komplikacje, abstrakcyjne pominięcie go pozwala w sposób bardziej przejrzysty przedstawienie proporcji zmian kierunku wektora prędkości.

Ponieważ mamy do czynienia z bryłą sztywną wektory prędkości tych punktów są zawsze równoległe ale ich długości będą różne.

W fazie równowagi wektor prędkości punktu A v=0. Punkty B i C poruszają się po orbitach a ich wektor prędkości są prostopadłe do pierwotnej osi obrotu i styczne do orbity. Siła dośrodkowa kręci ich wektorami prędkości wokół osi obrotu. Ten stan nazywam stabilnym ponieważ dopóki nie poruszymy obiektem stan ten będzie się utrzymywał.

Faza wybicia ze stanu równowagi.

Jeżeli teraz nawet nieznacznie pochylimy oś obrotu i rozkład mas jest odpowiedni, obecne interpretacje siły dośrodkowej możemy schować do szuflady. Jest ona już dla nas bezużyteczna. Jeżeli siła ta działała by w ten sposób jak obecnie ją rozumiemy, każdy obiekt obracał by się stabilnie wokół każdej osi obrotu gdyż siła ta jest zawsze skierowana prostopadle do tej osi. W rzeczywistości jednak obiekty z niesymetrycznym rozłożeniem mas w tej fazie zachowują się zupełnie inaczej. W tej fazie zadziałaliśmy zewnętrzną siłą by nieznacznie pochylić oś obrotu. Pytanie jest czy teraz wektor prędkości jest wciąż prostopadły do osi czy jednak lekko pochylony? Według mnie nie ma to tutaj większego znaczenia dlatego przyjmijmy że w przybliżeniu jest on prostopadły. Wektory prędkości punktów A, B i C są w przybliżeniu prostopadłe do pierwotnej osi obrotu.

Faza rozpędzania się fikołka.

W tej fazie mimo że nie działamy na obiekt żadną siłą zewnętrzną zaczyna się rozpędzanie zmiany kierunku wektora prędkość kątowej który zwiększa kąt pochylenia względem osi pierwotnej. W efekcie wektory prędkości punktów A, B i C zaczynają się pochylać w kierunku pierwotnej osi obrotu. Przy czym punkt A się rozpędza a punkt C hamuje. Przypomnę że na obiekt nie działa żadna siła zewnętrzna więc musi to być siła wewnętrzna. Siła o której nic nie wiemy.

Faza fiknięcia o 90 stopni.

Wektor prędkości punktu A osiąga swoje maksimum długości v=max zaś punktu C swoje minimum. Wszystkie wektory znajdują się na płaszczyźnie pierwotnej osi obrotu. Zakończyła się faza rozpędzania fikołka.

Faza hamowania fikołka.

Po przekroczeniu fiknięcia o 90 stopni zaczyna się faza odwrotna do przyspieszenia. Wektory prędkości zaczynają się ponownie pochylać w kierunku prostopadłym do pierwotnej osi obrotu jednak z przeciwnymi zwrotami. Przy czym teraz punkt C przyspiesza a punkt A zwalnia.

Faza końcowa

Obiekt dąży do pierwotnej osi obrotu jednak po fiknięciu zwrot wektora prędkości kątowej jest przeciwny.

Mamy więc następujące zmiany:

wektor prędkości punktu A z zerowej wartości zaczyna przyspieszać do maksimum które osiąga w połowie fazy po czym zaczyna zwalniać z powrotem do zera.

Wektora prędkości punktu C który na początku ma maksymalną wartość i zaczyna zwalniać w połowie fazy uzyskuje swoje minimum po czym zaczyna przyspieszać z powrotem do wartości maksymalnej.

Kąt pochylenia wszystkich wektorów względem osi pierwotnej zmniejsza się z 90 stopni do -90 stopni osiągając zero w połowie fazy.

Jak wygląda prędkość zmian pokazuje nam wykres zmian wektora prędkości kołowej umieszczony na blogu profesora Jadczyka.

http://arkadiusz.jadczyk.salon24.pl/718481,efekt-motyla-fiknie-czy-nie-fiknie.

Żółta linia to tempo zmiany kąta wektora v prędkości naszego punktu C zaś zielona i niebieska mogą być zmianami wektora v naszego punktu A.

Tak jak pisałem wcześniej tempo zmiany kąta wektora v jest śladem po działaniu siły. A więc pochodna po tej funkcji będzie siłą która jest przyczyną przyspieszenia.

Nie mam wszystkich wzorów ale wykres działania tej siły będzie wyglądał tak.

Teraz należy opisać tą siłę.

Mamy wzór na przyspieszenie kątowe

ɛ=dɷ/dt

oraz wzór na moment siły

M=I*ɛ

Czyli

ɛ=M/I

Mamy też wzory Eulera opisujące zmianę delta omega podczas efektu fikania

Ix(dɷx/dt)+(Iz-Iy)ɷzɷy=Mx

Iy(dɷy/dt)+(Ix-Iz)ɷxɷz=My

Iz(dɷz/dt)+(Iy-Ix)ɷyɷx=Mz

Tak zapisane wzory mogą mylić. Mx My i Mz są momentami sił zewnętrznych które w naszym przypadku równe są zero.

A więc wzory na delta omega powinny wyglądać tak

Daje nam to wzory na moment siły wewnętrznej odpowiedzialnej za fikołka

Mwx=(Iz-Iy)ɷzɷy

Mwy=(Ix-Iz)ɷxɷz

Mwz=(Iy-Ix)ɷyɷx

W naszym przypadku uzupełnijmy wzór na przyspieszenie kątowe następująco

Wiemy więc jak wygląda ta siła ale wciąż nie wiemy skąd ona się tam wzięła i co to za siła. Trzeba ją teraz zidentyfikować.

Notka ta jest kolejnym krokiem ale do końca jeszcze sporo pracy. Jak zawsze mam sporo pomysłów niestety potrzebuje na to czasu a ostatnio przyplątały się jeszcze problemy zdrowotne jednak efekt widzę coraz bardziej wyraźnie.

Zobacz galerię zdjęć: