Obrót ciała sztywnego - momenty sił z zachowaniem zasady momentu pędu.

Podczas spisywania na nowo wyników, znów okazało się że musiałem nanieść nowe korekty. Kiedy popełniasz błąd a nie ma nikogo kto mógłby ci go wskazać, to nie jesteś świadomy popełnianego błędu.

Gdzie był problem?

Wektor momentu pędu ma dwie postacie

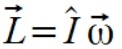     (1.a)

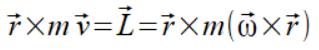     (1.b)

Wyciągając pochodną (1.a) dostajemy dwa człony z których jeden jest ewidentnym momentem siły i drugi człon który też okaże się momentem siły. O mechanice powstawania tych momentów sił za chwilę.

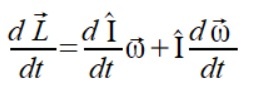    (2)

Dla zasady zachowania momentu pędu, moment siły jest równy ujemnej zmianie tensora momentu bezwładności na wektor prędkości kątowej

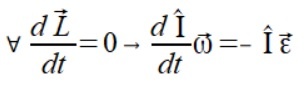    (2.a)

Mimo że jest to w sprzeczności z pewnym intuicyjnym wyobrażeniem wewnętrznych momentów siły, to jak widać we wzorze, istnienie wewnętrznego momentu siły nie jest sprzeczny z zasadą zachowania momentu pędu, a jest on niezbędny aby te prawo fizyki zachować. Jeżeli nie było by tego momentu siły to niezerowa zmiana tensora momentu bezwładności musiała by skutkować niezerową zmianą wektora momentu pędu.

I to właśnie ten minus przy wewnętrznym momencie siły sprawiał mi bardzo dużo problemów. Wcześniej na moim blogu wielokrotnie interpretowałem te momenty sił następująco:

Zmiana tensora momentu bezwładności (lewa storna (2.a)) tworzy moment siły który widzimy po prawej stronie równania (2.a) i takie rozwiązanie wydaje się intuicyjnie poprawne, ale w takiej interpretacji w moich obliczeniach ciągle nie uzyskiwałem minusa. Ponieważ w każdej weryfikacji liczba się zgadzała to jakoś podświadomie ignorowałem ten minus ale podczas mojego ostatniego spisywania wyników, tym razem bardziej solidnie zweryfikowałem swoje obliczenia aby znaleźć gdzie robię błąd. Błędem nie były rachunki a błędna była interpretacja ale o tym za chwilę.

Wyciągając pochodną ze wzoru (1.b) dostajemy inną postać pochodnej wektora momentu pędu.

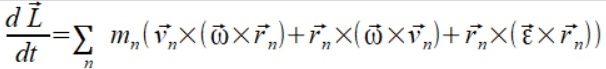(2.b)

Na poprzednich moich blogach udowadniałem już na kilka sposobów zgodność tych pochodnych (co nie jest żadnym zaskoczeniem), a zależności między tymi wzorami przedstawiam na poniższym diagramie

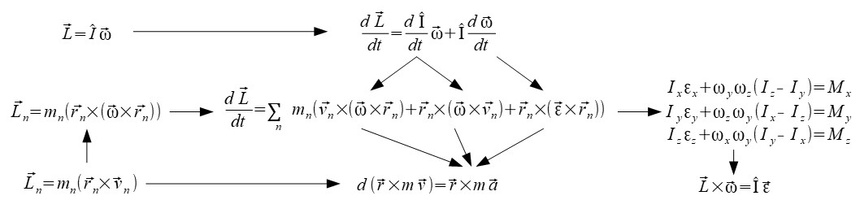(3)

Dla ruchu po orbicie eliptycznie mechanika powstawania tego momentu siły okazała się dość oczywista. Jak można przeczytać w każdym podręczniku, wektor przyspieszenia punktu ma dwie składowe:

-składową równoległą (przyspieszenie styczne a_s ) która zwiększa wartość wektora przyspieszenia

-składową prostopadłą (przyspieszenie dośrodkowe a_d ) która obraca wektorem prędkości.

Okazuje się że w trakcie ruchu po orbicie eliptycznej wektor prędkości punktu v (bez dwóch wyjątków) nie jest prostopadły do wektora przyspieszenia grawitacyjnego a_g, czyli przyspieszenie grawitacyjne możemy rozdzielić na składowe: styczne a_gs i "dośrodkowe" a_gd. Z tym że "dośrodkowe" należy rozumieć jako składową prostopadłą wektora przyspieszenia grawitacyjnego do wektora prędkości. "Dośrodkowe" znaczy do środka krzywizny w danym momencie, który to punkt nie musi się pokrywać ze środkiem układu.

Licząc wzór (2.a) okazuje się że pochodna tensora momentu bezwładności na wektor prędkości kątowej to jest moment siły wywołany grawitacyjnym przyspieszeniem dośrodkowym

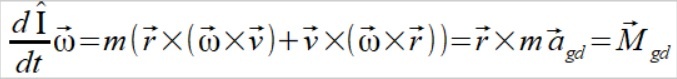(4.a)

Zaś moment siły z równania (2.a) to moment siły wywołany grawitacyjnym przyspieszeniem stycznym

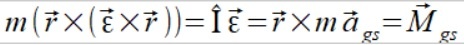(4.b)

Wektor przyspieszenia kątowego można wyliczyć wyciągając pochodną ze wzoru na prędkość kątową

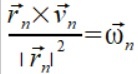(4.c)

Myślę że w tym przypadku każdy Fizyk który zrobi sobie te wyliczenia, szybko zrozumie zasadę działania i nie będzie ona budzić żadnych większych kontrowersji.

Szerzej opisałem to w linku poniżej

https://www.salon24.pl/u/przestrz/1158907,wlasnosci-wektora-przyspieszenia-w-odniesieniu-do-przyspieszenia-grawitacyjnego

Oraz wizualizacja mojej symulacji weryfikacyjnej

Jeżlei chodzi o obrót ciała sztywnego to wyniki moich obliczeń są bardziej skomplikowane i sprzeczne z tym co można by oczekiwać.

W ciele sztywnym punkty nie mogą się poruszać względem środka, czyli wektor prędkości punktu v_n będzie zawsze prostopadły do wektora położenia r_n . A co za tym idzie jeden człon równania (2.b) gdzie mamy iloczyn wektorowy wektora prędkości v_n na wektor prędkości powstały z iloczynu wektorowego prędkości kątowej ω na wektor położenia r_n , zawsze będzie równy zero.

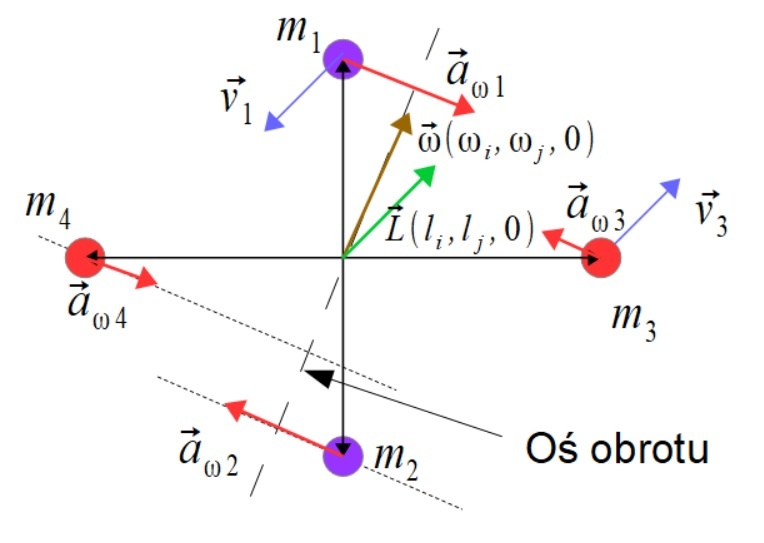
Drugi człon równania (2.b) daje nam przyspieszenia "dośrodkowe" które okazuje się się przyspieszeniem "doosiowym". Przyjęło się mówić że podczas obrotu ciała sztywnego, punkty obracają się względem środka ciężkości. Ale gdyby tak było, to punkty ciała sztywnego przemieszczały by się względem siebie. Tak naprawdę podczas obrotu ciała sztywnego punkty obracają się względem osi obrotu, która zazwyczaj jest chwilowa ale w niektórych przypadkach może być stała. Poniżej przykład takiej chwilowej osi obrotu.

Oraz wizualizacja symulacji wektorów prędkości i przyspieszeń punktów podczas efektu Dzanibekowa

Jak się okazało te przyspieszenia "doosiowe" mogą dawać niezerowy moment siły i tym okazał się drugi człon równania (2.b)

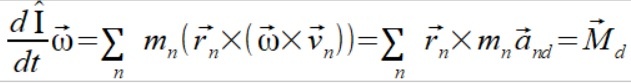(5.a)

Jak można przeczytać w książkach: przyspieszenie "dośrodkowe" (doosiowe) nie powoduje zmian wartości wektora prędkości i wektora prędkości kątowej i w uproszczeniu tym można by tłumaczyć brak przyspieszenia kątowego wywołany momentem siły (5.a).

Poniżej wizualizacja mojej symulacji pokazująca moment siły podczas efektu Dzanibekowa

I dochodzimy do momentu gdzie do tej pory robiłem błąd. Otóż zakładałem że moment siły (5.a) daje nam moment siły z prawej strony równania (2.a). Z tym że gdyby tak było to zmiana momentu pędu wywołana lewą stroną równania (2.a), zawsze by nam się podwajała. A jak to pokazuje wzór (2.a) powstały moment siły jest przeciwny do momentu siły (5.a).

Od razu powstaje pytanie: skąd punkty wiedzą jaki dokładnie moment siły (5.a) wytwarza prędkość kątowa (zmiana tensora momentu bezwładności) i co jest przyczyną powstania dokładnie odwrotnego momentu siły (prawa storna (2.a))?

Dla wielu wystarczyło by następujące wytłumaczenie: skoro zmiana tensora momentu bezwładności powoduję zmianę wektora momentu pędu, to musi powstać moment siły którą tą zmianę niweluje.

Tylko że w moim rozumowaniu punkty:

nie za bardzo mają świadomość,

nie za bardzo przejmują się zasadą momentu pędu

i nie mają możliwości wyliczyć jaka zmian wektora momentu pędu powstała,

tym bardziej nie mają też sposobności wytwarzać momentu siły z niczego.

Dla mnie zasada zachowania momentu pędu jest pewną ideą która zawsze się sprawdza a nie jest przyczyną jakiegoś skutku.

I teraz przejdę do mojej próby odpowiedzi na pytanie co jest przyczyną istnienia momentu siły i to pewnie ucieszy wielu miłośników "pozornej" siły odśrodkowej. Na wstępie dodam że doskonale rozumiem książkowy opis przyspieszenia odśrodkowego, gdzie będą na karuzeli, mimo że odczuwany przyspieszenie odśrodkowe (i jest to w pełni mierzalne) to mimo wszystko poruszamy się zgodnie z przyspieszeniem dośrodkowym. Ta dyskusja była wielokrotnie na moim blogu i zawsze trzymałem się książkowej wersji i nie widziałem w niej jakiś problemów.

Trzecie prawo Newtona mówi nam że akcja równa jest reakcji. Skoro karuzela przyciąga nas do środka to naszą reakcją jest działanie na karuzelę w przeciwnym kierunku. I być może jest to wytłumaczenie dla powstałego momentu siły (prawa storna (2.b)).

Zmiana tensora momentu bezwładności powoduje powstanie momentu siły (5.a) co jest akcją (przyczyną) i zgodnie z trzecim prawem Newtona powstanie dokładnie przeciwna reakcja która jest skutkiem tej akcji. Jednak teraz siła "pozorna" przestaje być pozorna.

Niechcący w końcu znalazłem jakiś punkt zaczepienia do weryfikacji eksperymentalnej moich wyliczeń. Do tej pory nikt nie pokazał jakiś błedów w moich wyliczeń ale było pytanie jak je zweryfikować eksperymentalnie?

Teraz w końcu można zaprojektować obracające się ciało sztywne i umieścić na tam czujniki mierzące wektory przyspieszeń w tych punktach i po prostu sprawdzić uzyskane pomiary zgadzają się z moimi wyliczeniami.

P.S.

Jeżeli masz jakieś pytanie to po prostu napisz komentarz.