Kiedy zaczynałem moja przygodę z tym tematem nawet mi się nie marzyło że będę umiał rozkładać takiego potwora jak rachunek tensorowy na tak drobne szczegóły i opanuję ten temat na tyle dobrze aby niektóre wyliczenia robić w głowie. Potrzeba matką wynalazku, praktyka czyni mistrza i umiesz liczyć licz na siebie.
Myślałem że już będę potrafił na podstawie wektorów przyspieszeń zrobić obroty ale praktyka pokazała że jeszcze nie teraz. Zanim dokonam obrotu muszę bardziej zgłębić tajemnice tensora.
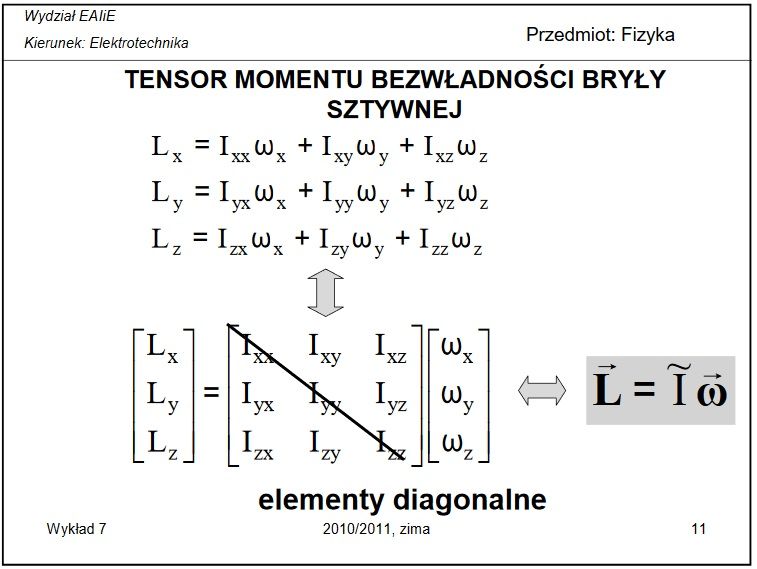

Wiem że wygląda on strasznie ale jak się go pozna to jest całkiem miły stworek.
Rozpatrzmy najprostszą sytuacje punkt obraca się na płaszczyźnie XY wokół osi Z
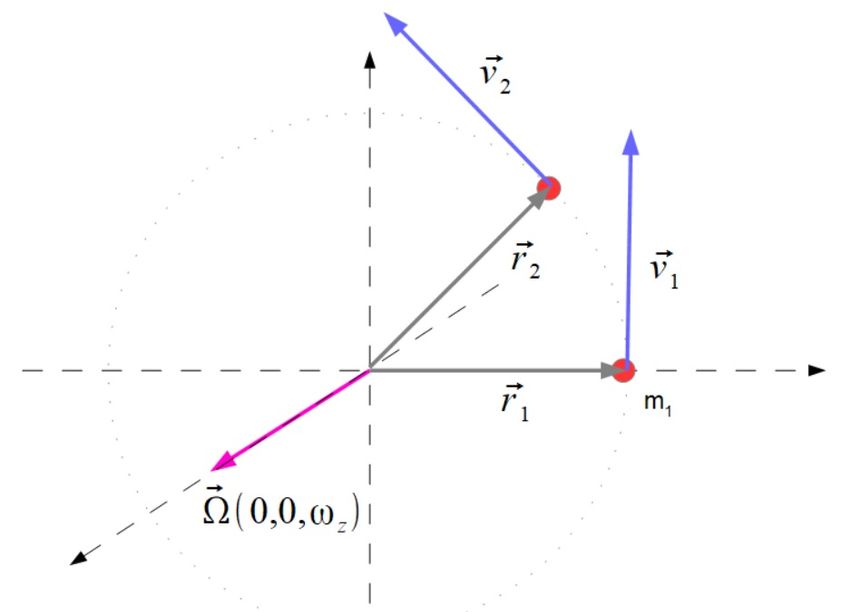
Bardzo przyjemny przykład bo z dziewięciu elementów tensora zaledwie jeden jest niezerowy Izzωz i możemy się mu lepiej przyjrzeć.
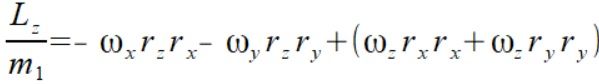
(1)
Bardzo ważne jest wychwycić każdy szczegół gdyż matematyka jest tworem idealnym, nie wybaczającym żadnej nawet najmniejszej pomyłki lub pominięcia i nie da się osiągnąć prawidłowego wyniku robiąc jakiś element źle. Nieraz nad jakimś elementem marnowałem wiele dni gdyż umykał mi jakiś detal. Teraz dość szybko się zorientowałem że licząc moment pędu nie możemy go zapisać Lz=rx*vy+ry*vx a musimy to zapisać zgodnie z iloczynem wektorowym Lz=rx*vy-ry*vx. Patrząc na r2 minus nie oznacza że odejmuje się dwie wartości a jest to kierunek działania iloczynu wektorowego.
Zapis (1) za pomocą iloczynu wektorowego pamiętając że ωx=0 i ωy=0
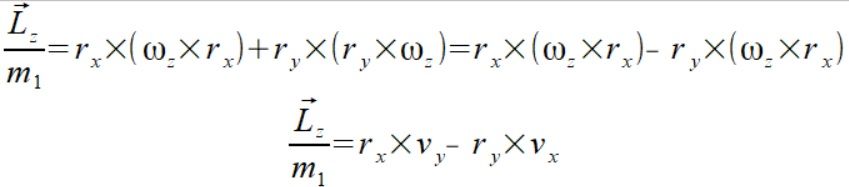
(2)
Zastosuje teraz mój wzór na pochodną
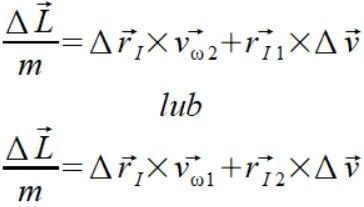
(3)
Dostałem dwa wzory i długo się zastanawiałem który jest ten właściwy. Dzisiejszy przykład rozstrzyga że to ten pierwszy jest prawidłowy a zastosowanie drugiego nie daje poprawnego wyniku.
Licząc pochodną wzoru (2) na bazie (3) otrzymujemy
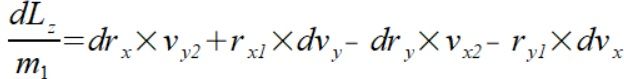
(4)
Zweryfikowałem to pozytywnie na kilku przykładach a oto jeden z nich
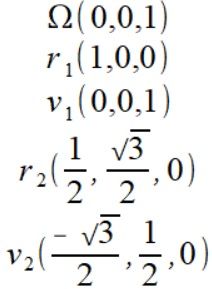
Podstawiamy do wzoru (4)
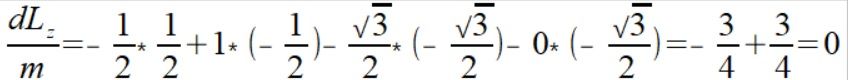
Od razu dowód że zawsze będzie zero. Współrzędne wektorów
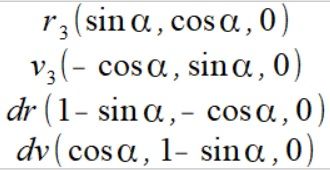
Wstawiamy do wzoru (4)
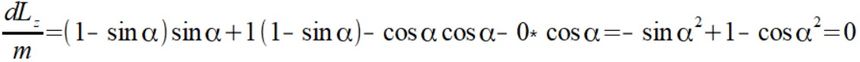
Inne tematy w dziale Technologie

