Rachunek sprawdzający v x p = r x F

Najważniejsze we wzorach to to aby działały poprawnie a wzór który podałem ostatnio nie daje poprawnych wyników

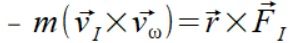
(1)

https://www.salon24.pl/u/przestrz/1059942,dalsza-analiza-wektora-momentu-pedu

Na tym etapie zazwyczaj wszystko wyliczam i nie ma już zgadywania ale tym razem intuicja mi podpowiadała że czego w tym wzorze brakuje. Na intuicje trzeba uważać bo często jest błędna i wyprowadza cię w pole ale zdarza się czasami że jak nie wiesz w którą stronę podążać to intuicja wskaże ci prawidłowy kierunek. Nauczony doświadczeniem z poprzednich wyliczeń uzupełniłem wzór (1) następująco

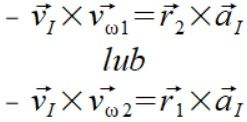
(2)

Gdzie indeks 1 jest stanem początkowym zaś indeks 2 stanem końcowym. Jeszcze nie wiem dlaczego akurat tak ale mam zamiar się dowiedzieć.

Udało mi się już wyprowadzić ten wzór tutaj

https://www.salon24.pl/u/przestrz/1060739,wyprowadzenie-dri-x-p-1-ri2-x-fi-z-pochodnej-wektora-momentu-pedu

Rachunek sprawdzający

Przykład pierwszy

r₁=1;       ω₁=1;     m=1

mamy więc

I₁=1;        L=1;        v_ω1=1

teraz zwiększamy r dwukrotnie

r₂=2;        I₂=4;       ω₂=1/4;

L=I₁ω₁=I₂ω₂;

v_ω2= ω₂ x r₂= 1/2

dr=1=v_I;        dv=-1/2=a_I

Podstawiamy do (2)
- (1 x 1) = 2 x -1/2

zwiększamy r trzykrotnie

r₃=3; I₃=9; ω₃=1/9;

L=I₁ω₁=I₃ω₃;

v_ω3= ω₃ x r₃ = 1/3

dr=2; dv=-2/3

Podstawiamy do (2)
- (2 x 1) = 3 x -2/3

zwiększamy r dziesięciokrotnie

r₄=10; I₄=100; ω₄=0,01;

v_ω4= ω₄ x r₄ = 0,1

dr=9; dv=0,9

Podstawiamy do (2)
- (9 x 1) = 10 x -0,9

Przykład drugi

Mamy dane wyjściowe

r₁=4;       ω₁=1;     m=1

co daje nam

I₁=16;        L=16;        v_ω1=4

teraz zmniejszamy r o połowę

r₂=2;        I₂=4;       ω₂=4;

L=I₁ω₁=I₂ω₂;

v_ω2= ω₂ x r₂ = 8

dr=-2;        dv=4

Podstawiamy do (1)

- (-2 x 4) = 2 x 4

zmniejszamy r czterokrotnie

r₃=1;      I₃=1;         ω₃=16;

L=I₁ω₁=I₃ω₃;

v_ω3= ω₃ x r₃ = 16

dr=-3;        dv=12

Podstawiamy do (1)

- (-3 x 4) = 1 x 12