Nie wiem czemu w książkach poniższy wzór jest nazywany tensorem momentu bezwładności kiedy tensor ten jest jedynie częścią wzoru na wektor momentu pędu
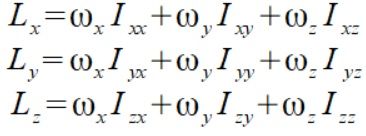
(1)
Dla mnie to właśnie w pochodnej tego wzoru są ukryte wszystkie szczegóły ruchu obrotowego ciała sztywnego które gdzieś umknęły współczesnej nauce. Mimo że lekarstwa dokuczają i bardzo utrudniają koncentracje udało się rozpisać ten wzór w miarę prostej postaci, chociaż jak za chwilę się okaże "prosta postać wzoru" jest pojęciem względnym.
Aby było bardziej przejrzyście rozpiskę tą robię dla jednego punktu m1 . Żeby pokazać bryłę sztywną w mojej opinii potrzebujemy co najmniej dwa takie punkty na prostopadłych do siebie ramionach, a zapewne znajdą się i tacy którzy stwierdzą że dla poprawności potrzebne będzie minimum sześć takich punktów, po dwa na każdej głównej osi bezwładności.
Rozłóżmy więc wektor momentu pędu na czynniki pierwsze dla m1
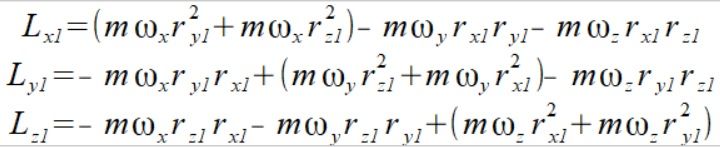
(2)
Szczegóły w prezentacji slajd12 str6
http://home.agh.edu.pl/~zak/downloads/7bryla-2010.pdf
Zróbmy teraz kilka przekształceń
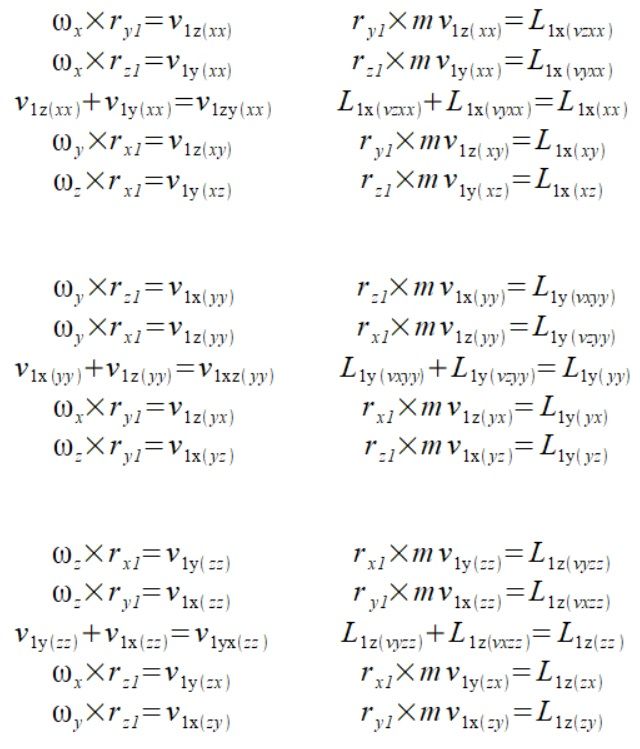
(3)
Dokonałem teraz następujące przekształcenie wzoru (2) oraz jej postać macierzową która jest bardziej przejrzysta
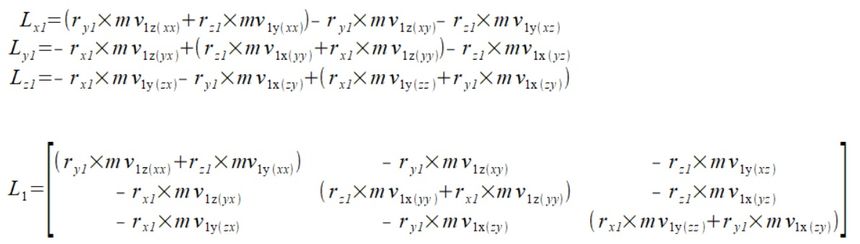
(4)
Teraz można w miarę "łatwo" ;) wyliczyć pochodną wektora momentu bezwładności dla tego jednego punktu
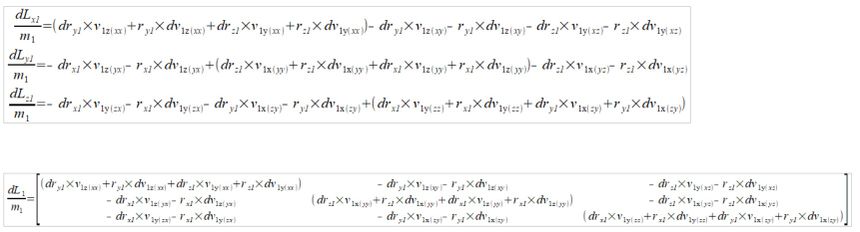
(5)
Teraz trzeba będzie pokazać że jest zachowany moment pędu dla całej bryły sztywnej czyli co najmniej dwóch specjalnych punktów a wielu będzie twierdzić że co najmniej dla sześciu.
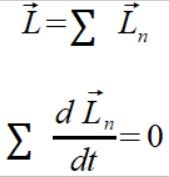
(6)
Istnienia dwóch przeciwstawnych momentów siły
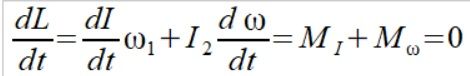
(7)
Oraz niezerowego przyspieszenia kątowego zgodnego ze wzorem
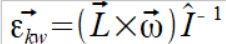
(8)
Czy matematyka nie jest piękna w swej prostocie?;)
Inne tematy w dziale Technologie

