Zadziwiające jak dużo czasu trzeba poświecić aby znaleźć rozwiązanie które okazuje się bardzo proste i oczywiste. To tak samo jak powiedziano Kolumbowi że odkrycie Ameryki było bardzo proste ponieważ wystarczyło jedynie popłynąć na zachód. Problem polegał na tym że nikt wcześniej się na to nie odważył, a sam Kolumb aby dokonać tego prostego odkrycia poświęcił pół życia aby przekonać tych którzy decydują że warto to zrobić. Czyli przekonanie innych że warto, było dużo bardziej skomplikowane i trudniejsze aniżeli sama wyprawa dokonująca przełomowego odkrycia.
Wyniki mojej pracy raczej wielkim przełomom nie są, chociaż na obecnym etapie trudno przewidzieć czy będzie to użyteczne czy jedynie uzupełnienie obecnej wiedzy. To tak samo jak ci co eksperymentowali z prądem, benzyną czy pierwiastkami radioaktywnymi nie mogli przewidzieć jak ich odkrycia zostaną wykorzystane w przyszłości. To jednak borykam się z podobnymi problemami co Kolumb, nikt nie widzi sensu moich dociekań, brak jakiegoś wsparcia czy pomocy, za to pełno jest ignorancji i zadufania że niby nic tam nie ma, tak samo jak na zachodzie miała być krawędź ziemi i nic ponadto.
Od dłuższego czasu staram się zrozumieć jak zmiana momentu bezwładności wpływa na prędkość punktu. Podręcznikowe wyjaśnienia są dla mnie niewystarczającym opisem, nie odpowiadającym na wszystkie pytania. Potrzebuje wiedzieć bardziej dogłębnie i chce umieć odpowiedzieć na wszystkie pytania jakie umiem sobie wyobrazić, a nie segregować pytania na te właściwe które umiem odpowiedzieć i na te źle zadane ponieważ nie znam na nie odpowiedzi, a to typowa retoryka mądrych tego świata.
Wychodzimy z zasady zachowania momentu pędu
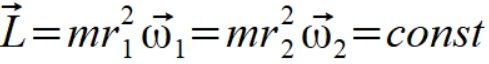
W temacie mechaniki bryły sztywnej bardzo złożonym tematem jest wartość wektora położenia r i jest to chyba najtrudniejsze zagadnienie, gdyż poprawne dobranie wartości r jest kluczowe dla prawidłowego wyniku a w kilku sytuacjach mamy do wyboru kilka interpretacji wartości r i trzeba wiedzieć który r jest ten właściwy. Wszystkie inne wartości są dość proste w zastosowaniu i intuicyjne ale z wektorem położenia często jest problem i tym razem również powstaje paradoks że mamy różne skutki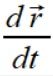 
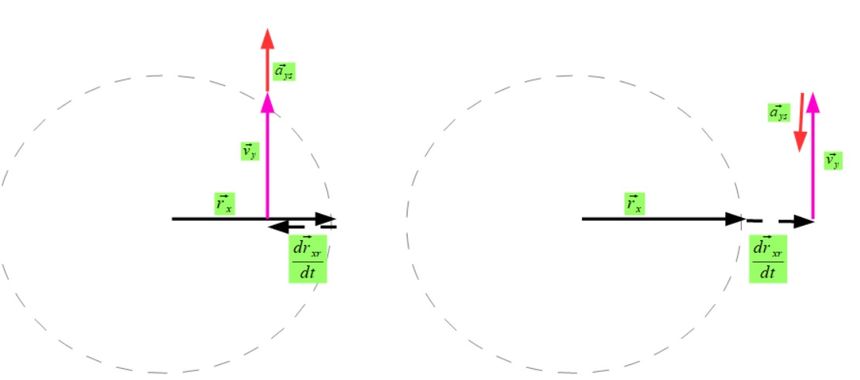
Musimy tu przeanalizować ruch po okręgu. Mamy więc punkt który ma swój wektor prędkości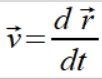 
oraz działające na niego przyspieszenie dośrodkowe 
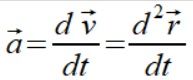. Przerobiłem nieco zrzut ekranu na potrzeby tej notki z kursu Youtube Fizyka
https://www.youtube.com/watch?v=ic_46x3Z3X4&t=768s
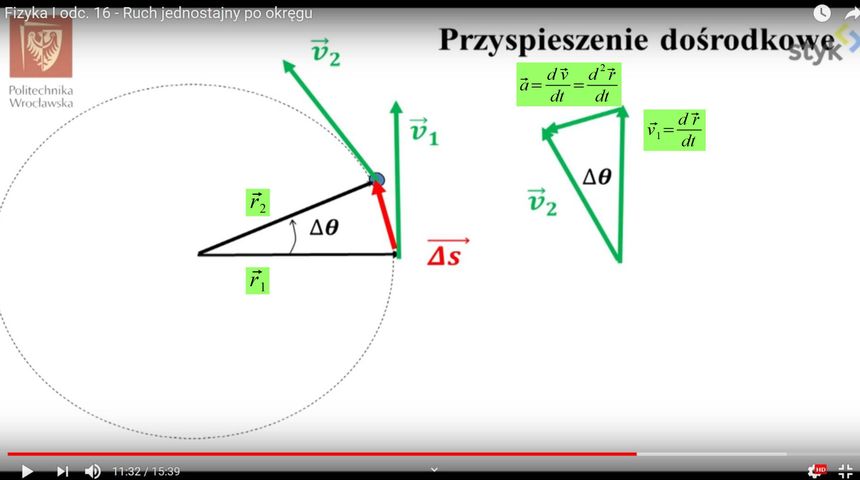
Trzeba pamiętać że jest to uproszczony schemat dla dość dużego dt i w rzeczywistości wektor przyspieszenia a w tym przypadku jest prostopadły do wektora prędkości v. Zauważmy też ze w tym przypadku wektor położenia ma zawsze tą samą wartość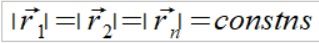 
Aby nieco uprościć i bardziej uwidocznić co che pokazać dobieramy układ odniesienia gdzie wektor położenia zawsze będzie się znajdował na jednej z osi.
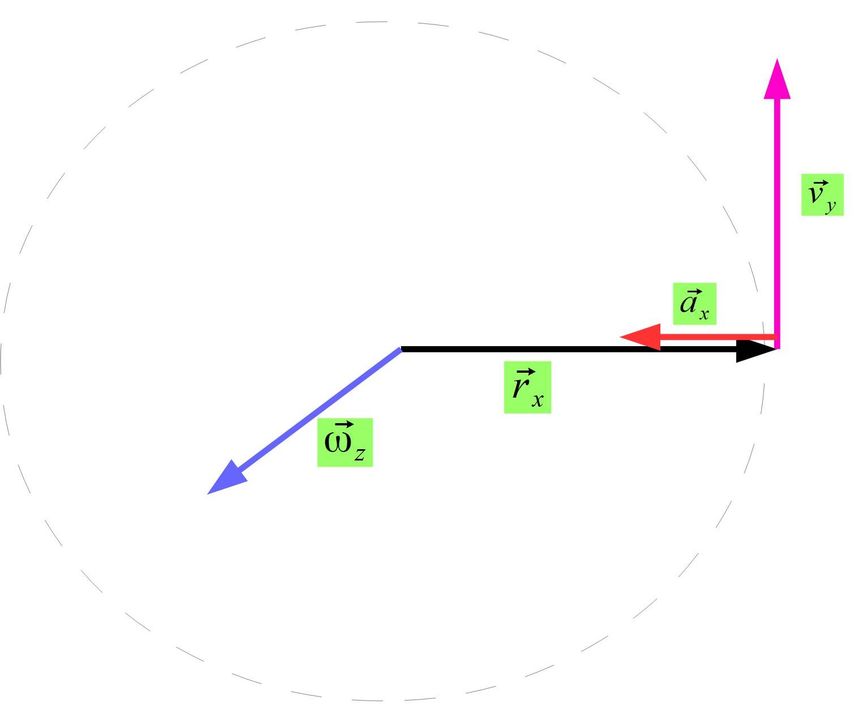
Po raz kolejny wychodzimy z zasady zachowania momentu pędu
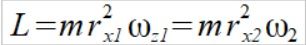
Zauważmy że
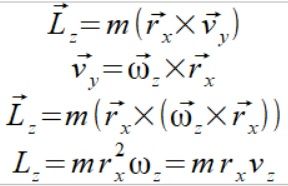
Możemy teraz bez zbędnych pierwiastków wyprowadzić wzory na wartości r
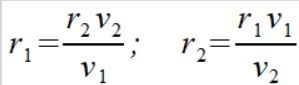
Możemy teraz sprawdzić czym jest różnica wartości r która przypomnę jest odległością punktu od osi obrotu I=mr2
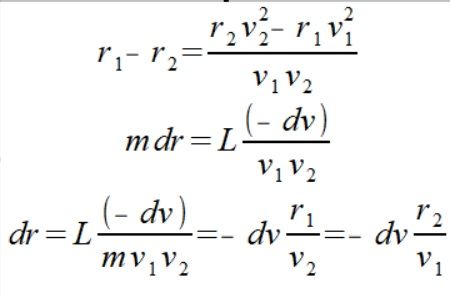
Aby było łatwiej wprowadźmy zmienną proporcji x
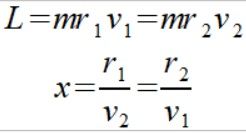
Jeżeli ktoś kiedyś na poważnie przeanalizuje moje wcześniejsze wzory to co mnie zaskoczyło (mimo że wielu twierdzi odwrotnie) to brak jakiekolwiek sprzeczność z obecnymi wzorami. Dokonałem jedynie prostych i oczywistych przekształceń których nie wiadomo czemu nikt wcześniej nie odważył się sprawdzić. Tym razem powstaje wzór który nie widziałem w żadnym podręczniku czy materiale który czytałem. To że ze zmianą momentu bezwładności wiążą się zmiany prędkości punktu wiedza wszyscy ale nigdy nie widziałem równania które to opisuje a wygląda ono następująco dla naszego przykładu
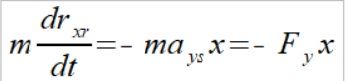
Gdzie
drxr jest zmianą wektora położenia równoległą do tego wektora
ays jest przyspieszeniem stycznym punktu
Zachodzi tu te dziwne zjawisko że kiedy zmniejszamy moment bezwładności drxr to otrzymujemy prostopadłe do tej zmiany przyspieszenie punktu ays
Inne tematy w dziale Technologie
