Niestety po dłuższej przerwie nie mogę powrócić do pewnego kreatywnego stanu umysłu który pozwalał mi w pełni skoncentrować się na zagadnieniu które mnie interesuje i poprzez analizę różnych pomysłów szukać prawidłowych rozwiązań. Niestety mimo że ostatnio mam trochę czasu i mimo że wiem co chciałbym zrobić to nie umiem się skupić aby było to efektywne i posunęło mnie trochę do przodu.
Rozwinę więc odpowiedź na pytanie Eine na czym polega różnica miedzy przyspieszeniem kątowym zewnętrznym a wewnętrznym i jak te przyspieszenia oddziałują na punkt. Właściwie ta notka jest skrótowym opisem moich konkluzji wynikających z analizy mechaniki obrotu ciał sztywnych.
Zacznijmy od początku. Punkt w danej chwili ma swój wektor położenia r0 który wraz z upływem odcinka czasu dt może ulec zmianie r1. Różnica wektorów położenia wyznacza wektor prędkości kątowej
Jednak wektor prędkości v0 również po chwili dt może zmienić swoją wartość v1 a różnica wektorów prędkości tworzy wektor przyspieszenia

Jak pokazały wyliczenia matematyczne, co i później potwierdziła praktyka zmianę wektora w czasie ma pewną ciekawą własność która całkowicie jest sprzeczna z ludzką intuicją, którą ja również bardzo długo nie umiałem zrozumieć. Otóż kierunek zmian wektora ma bardzo duże znaczenie. Jak się okazało jeżeli zmiana jest wzdłuż wektora to wektor zmienia wartość ale nie zmienia kierunku, natomiast jeżeli zmiana jest prostopadła do wektora to wektor zmienia swój kierunek ale nie zmienia wartości.
Bardzo dobrze to widać na przykładzie wektora przyspieszenia i dlatego mamy dwa rodzaje przyspieszeń: styczne które zmienia wartość wektora prędkości i dośrodkowe (prawidłowo doosiowe) które zmienia kierunek wektora prędkości.

Nie będę tu wchodził w szczegóły można je znaleźć w każdym podręczniku czy na Wikipedii
https://pl.wikipedia.org/wiki/Przyspieszenie.
Dodam tutaj że każda zmiana wektora w czasie każdej wielkości odbywa się w taki sam sposób. Jeżeli jest ona wzdłuż wektora to zmienia ona jego wartość ale nie wpływa na kierunek, natomiast jeżeli jest prostopadła do wektora to zmienia jego kierunek ale nie zmienia wartości wektora.
Wektor prędkości kątowej ω jest to szczególny przypadek prędkości, gdzie na wektor prędkości punktu v działa przyspieszenie dośrodkowe

Uprośćmy (stwierdzenie te nie zawsze będzie prawdziwe) gdy prędkość kątowa jest stała czyli wektor ten nie zmienia swojej wartości w czasie, to wektor prędkości punktu v nie będzie zmieniał swojej wartości a jedynie zmieniać się będzie kierunek jego działania i zawsze będzie mu towarzyszyć prostopadłe do niego przyspieszenie dośrodkowe ad które również nie będzie zmieniać swej wartości, IvI=constans IadI=constans. Wektory prędkości kątowej, prędkości i przyspieszenia dośrodkowego zawsze będą do siebie prostopadłe.
Po wprowadzeniu wyjaśniamy działanie przyspieszenie kątowych zewnętrznych.
Jeżeli na obiekt działa siła zewnętrzna Fc=Fd+Fm to składowa tej siły skierowana do środka ciężkości Fd spowoduje zmianę prędkości układu ale nie wywołuje momentu siły, zaś pozostała składowa siły Fm nie wpływa na przyspieszenie środka ciężkości ale skutkuje powstaniem zewnętrznego momentu siły

Mamy więc teraz zewnętrzny moment siły wywołany oddziaływaniem zewnętrznym i towarzyszące mu zewnętrzne przyspieszenie kątowe

Bierzemy przykład kiedy wektor położenia ma stałą wartość w czasie czyli też moment bezwładności jest stały. Przyspieszenie kątowe ε jest to zmiana wektora prędkości kątowej ω w czasie ε=dω/dt i podlega tym samym własnością co każdy inny wektor, czyli zmiana wektora prędkości kątowej ω wzdłuż tego wektora powoduje zmianę wartości tego wektora ale nie zmienia on swojego kierunku, natomiast przyspieszenie prostopadłe do wektora prędkości kątowej ω zmienia jego kierunek ale nie zmienia jego wartości. Od razu podaje wzór na wektor przyspieszenia punktu


Działanie zewnętrznego momentu siły zawsze zostawia ślad w postaci zmiany wektora momentu pędu ale znów zmiana ta jest zależna od kierunku działania. Jeżeli moment siły działa wzdłuż wektora momentu pędu to zmienia się wartość wektora momentu pędu ale nie zmienia się jego kierunek działania, moment siły działa efektywnie i zmienia energię układu dlatego też zmienia się wartość momentu pędu. Jednak kiedy moment siły działa prostopadle do wektora momentu pędu to zmienia się kierunek momentu pędu ale jego wartość pozostaje taka sama, taki moment siły jest nieefektywny znaczy się nie zmienia wartości energii układu i wartość momentu pędu pozostaje stała.
Wewnętrzne przyspieszenie kątowe.
Jednak zmiana prędkości kątowej nie musi być wynikiem oddziaływań zewnętrznych a może się ona odbyć w odizolowanym obiekcie po przez oddziaływania wewnątrz obiektu.
Pierwszym takim przykładem są obiekty potrafiące zmienić swój moment bezwładności, na przykład łyżwiarka robiąca piruet. Ponieważ nie ma ingerencji zewnątrz moment pędu takiego obiektu jest stały i skoro moment bezwładności uległ zmianie to aby zachować zasadę zachowania momentu pędu również prędkość kątowa musi się zmienić a zmiana prędkości kątowej w czasie jest przyspieszeniem kątowym
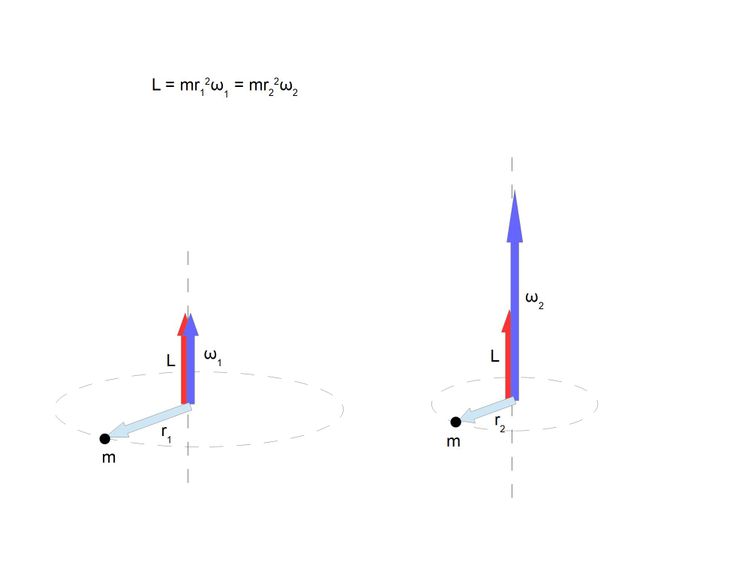
A wynika to z zasady zachowania momentu pędu

Możemy teraz wskazać wewnętrzne przyspieszenie kątowe
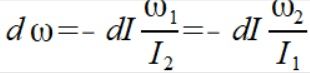
Widzimy tu dwa przeciwstawne momenty sił które się zerują nie powodując zmiany wektora momentu pędu w czasie i jednocześnie istnieje niezerowe przyspieszenie kątowe.
Wiele osób zarzuca mi że skoro moje wyniki pokazują niezerowe wewnętrzne przyspieszenia kątowe to muszą one być sprzeczne z prawami Fizyki, nie rozumieją oni że przyspieszenia takie są niezbędne aby obecne prawa Fizyki utrzymać i wynikają one z tych praw które rzekomo łamią.
Jeżeli chodzi o detale tego ruchu i wyznaczenia wektora przyspieszenia dla punktu, to jest to obecnie tematem mojej analizy i nie poznałem jeszcze wszystkich tajemnic tego przypadku. Trzeba odpowiedzieć czym jest zmiana momentu bezwładności w czasie dI/dt i jak tworzy ona moment siły. Zauważmy że zmieniając moment bezwładności działamy przyspieszeniem dośrodkowym prostopadłym do wektora prędkości a uzyskujemy przyspieszenie styczne (zmiana prędkości kątowej)
Moje wyliczenia powyższych wzorów
https://www.salon24.pl/u/przestrz/924974,wyprowadzenie-wzorow-na-wewnetrzne-przyspieszenie-katowe
oraz konkretne przykłady
Inny przykładem istnienia wewnętrznych przyspieszeń kątowych jest obrót ciał sztywnych z różnymi głównymi momentami bezwładności. Często występuje wtedy sytuacja że wektor momentu pędu i prędkości kątowej nie są równoległe, co ma swoje konsekwencje.

W tym przypadku składowa prędkości kątowej prostopadła do wektora momentu pędu powoduje jego obrót co musi wiązać się z powstaniem momentu siły, jednak również i tutaj powstaje zmian tensora momentu bezwładności która generuje drugi przeciwstawny moment siły

Rozpatrujemy swobodną bryłę dlatego moment sił zewnętrznych Mz=0 i mamy teraz nasze momenty siły z których można wyliczyć wewnętrzne przyspieszenie kątowe

To jak to działa pokazuje wyliczenie iloczynu wektorowego dla konkretnego przykładu

Mechanizm działania jest następujący. Każdy punkt bryły sztywnej ma składową prędkości kątowej która jest prostopadła i równoległa do wektora położenia. Składowa prostopadła do wektora położenia wywołuje przyspieszenie dośrodkowe jakie mamy opisane w każdym podręczniku, jednak mamy jeszcze składową prędkości kątowej równoległą do wektora położenia i prędkość ta obraca punktem wraz z jego wektorem prędkości skutkując powstania dodatkowego przyspieszenia, który skutkuje powstaniem momentu siły.
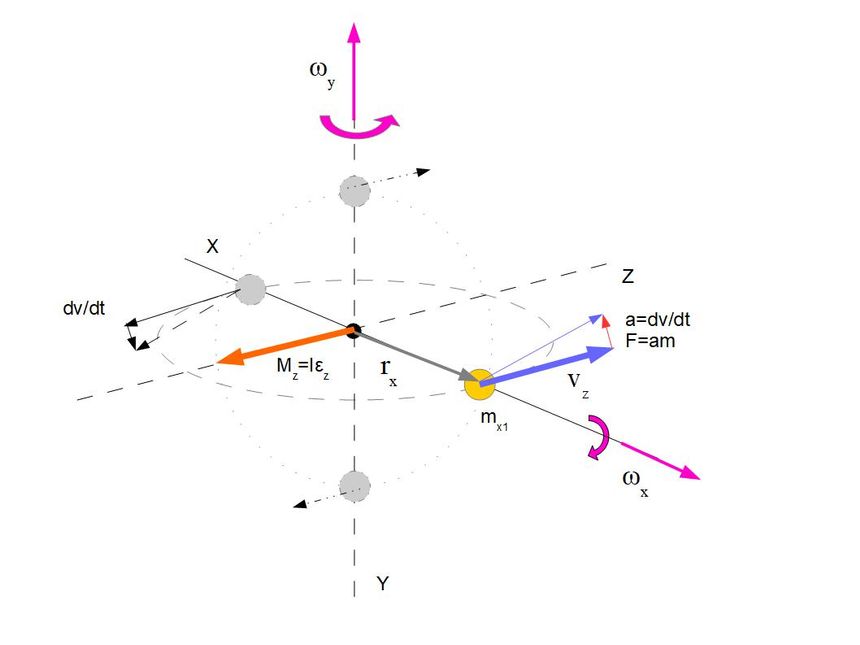
Działanie tego momentu siły jak i przyspieszeń kątowych można zobaczyć na moich symulacjach
Jest to bardzo skrótowy opis moich wyników, o wiele więcej detali jest w moim opracowaniu które nadal jest wersją roboczą, które nadal zawiera drobne błędy które sukcesywnie znajduje i poprawiam.
https://megawrzuta.pl/download/9d64933e917f67752e1cb986516a320d.html







Komentarze
Pokaż komentarze (4)