Rachunki wewnętrznego przyspieszenia kątowego na konkretnych przykładach.

    Kontynuuje poszukiwanie rozwiązania pochodnej tensora momentu bezwładności na wektor krętu

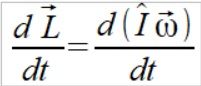    (1)

    Niestety robiąc to tradycyjnie wychodzą mi koszmarnie długie równania matematyczne w których nie umiem znaleźć uproszczeń by sprowadzić je do prostej postaci którą mogli by zrozumieć nawet amatorzy. W linijkach wzoru gdzie są całe masy zmiennych nie umiem dostrzec sensu który pozwoliłby mi to uprościć, a jednym z moich celów jest przedstawić te  zagadnienie na tyle prosto aby mógł to zrozumieć licealista i wszystkie pozostałe wyniki udało mi się już sprowadzić do tak prostej postaci. Jeżeli ktoś wie jak wygląda rozwiązanie tej pochodnej to będę wdzięczny za informacje.

    Ponieważ moja wiedza nie wystarcza jeszcze do rozwiązań w trójwymiarze wracam do analizy dwuwymiarowego przykładu który wyliczyłem w notce

https://www.salon24.pl/u/przestrz/924974,wyprowadzenie-wzorow-na-wewnetrzne-przyspieszenie-katowe

    Oto zastosowanie wzorów na konkretnych przykładach.

    Wzór na zmianę przyspieszenia kątowego dla ruchu płaskiego dwuwymiarowego

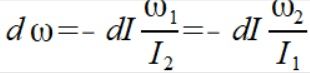  (2)

oraz wzór na pochodną momentu pędu dla ruchu płaskiego dwuwymiarowego

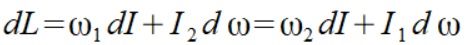        (3)

    Mamy początkową i końcową prędkość kątową ω₁ ω₂, początkowy i końcowy wektor położenia r₁ r₂ i masę punktu który dla uproszczenia będzie się równał jeden m=1.

ω₁=4

r₁=2

Liczymy moment pędu

L=mr₁²ω₁=16

zwiększamy teraz wektor położenia do wartości końcowej

r₂=4

musimy teraz wyliczyć prędkość kątową dla dla tego wektora położenia

L=mr₁²ω₁=mr₂²ω₂

ω₂=L/(mr₂²)=1

liczymy momenty bezwładności

I₁=mr₁²=4

I₂=mr₂²=16

liczymy różnice wartości prędkości kątowej i momenty bezwładności

dω=ω₁-ω₂=3

dI=I₁-I₂=-12

Wstawiamy wartości do wzoru (2)

 dω=-(-12)(1/4)=3

wstawiamy wartości do wzoru (3)

dL=4(-12)+16*3=1(-12)+4*3=0

    Dla tego przykładu wzory dały poprawny wynik. Spróbujemy jednak dla innego przykładu

m=1; r₁=1; w₁=4;

czyli

L=4

zwiększamy wektor położenia do

r₂=3; ω₂=4/9

I₁=1; I₂=9

dω=32/9

dI=-8

Używamy wzoru (2)

dω=-(-8)4/9=32/9

używamy wzoru (3)

dL=4(-8) + 9(32/9)=(4/9)(-8)+1*32/9=0

Znowu wzory okazały się poprawne. Całe wyprowadzenie tych wzorów znajduje się w linku który jest na początku tej notki.