Przyjemna interpretacja tensora momentu bezwładności na wektor prędkości kątowej.

    Zmęczenie tematem, perypetie życiowe i wszechobecne próby zniechęcenia mnie do szukania rozwiązań spowodowało że ostatnio trochę odpuściłem. Jednak trzeba dokończyć parę rzeczy.

    Najistotniejszą rzeczą jaką muszę jeszcze udowodnić jest wyliczenie pochodnej tensora momentu bezwładności na wektor prędkości kątowej

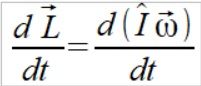  (1)

dla zasady zachowania momentu pędu

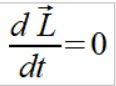 (2)

Wyliczenia te dla przestrzeni dwuwymiarowej (efekt piruetu łyżwiarki) okazały się nadzwyczaj proste

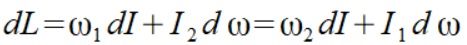 (3)

i można je znaleźć tutaj

https://www.salon24.pl/u/przestrz/924974,wyprowadzenie-wzorow-na-wewnetrzne-przyspieszenie-katowe

Jednak dla przestrzeni trójwymiarowej sytuacja bardzo się komplikuje gdyż

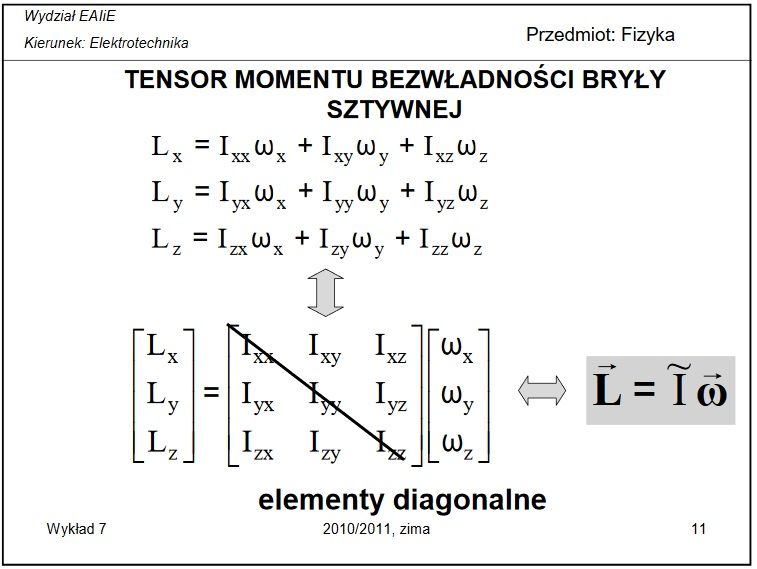   (4)

   (5)

Link do prezentacji

http://home.agh.edu.pl/~zak/downloads/7bryla-2010.pdf

    Jeżeli ktoś umie wyciągnąć pochodną z równania (1) będę wdzięczny za wyjaśnienia. A jeżeli kogoś na widok tych równań rozbolała głowa to mogę potwierdzić że jest to całkiem naturalne :) Polecałbym też doczytanie do końca bo pokaże całkiem miłą i przyjemną interpretacje tego matematycznego potwora. Poświęciłem masę czasu na zrozumienie tego, wpatrując się w te znaki szukałem prostych powiązań które tłumaczyły by te wzory, a rozwiązanie jak zawsze wcześniej okazało się banalne i aż głupio że nie widziałem tego wcześniej :)

    Wykorzystałem technikę która wielokrotnie się już sprawdziła w moich rachunkach. Dobieram układ odniesienia aby uzyskać jak najwięcej zer dla dwóch punktów znajdujących się na dwóch prostopadłych do siebie ramionach.

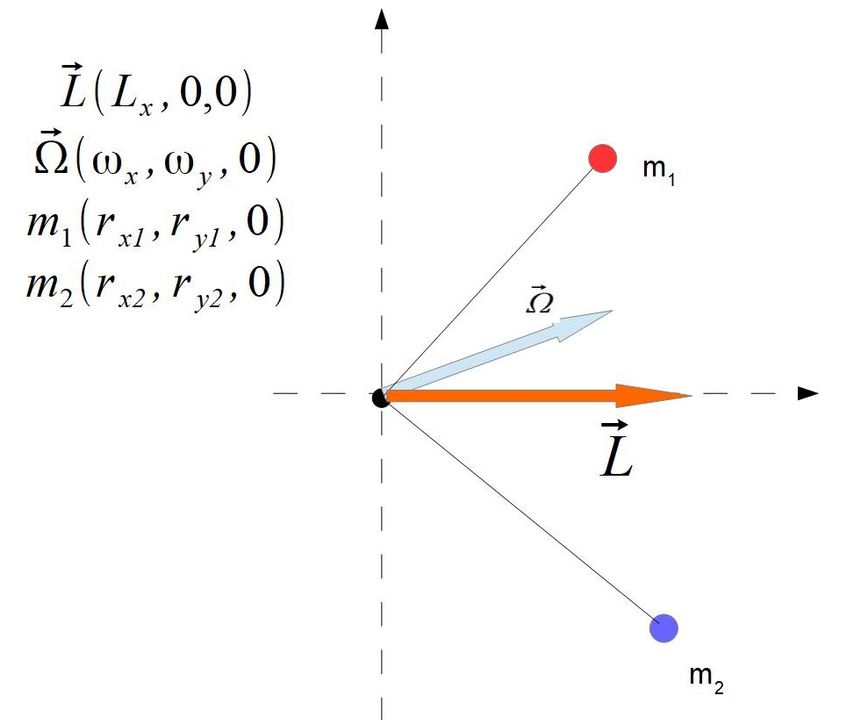
Aby było łatwiej masy punktów są sobie równe

m₁=m₂=m

Mamy tylko jedną składową wektora krętu co bardzo ułatwia sprawę bo L_y=0 i L_z=0. Z równań (4) (5) otrzymujemy

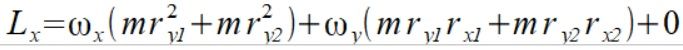  (6)

i policzmy teraz L_x jedynie dla jednego punktu

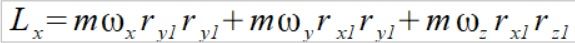  (7)

prosta zależność

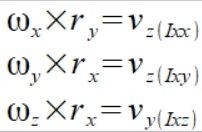  (8)

i mamy rozwiązaną zagadkę równania tensora momentu bezwładności na wektor prędkości kątowej

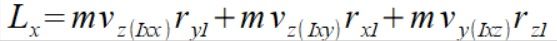  (9)

co już łatwo zinterpretować jako

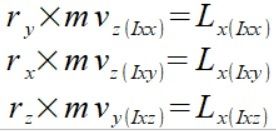
(10)

Aby lepiej zrozumieć opis.

    Wektor prędkości kątowej ma trzy składowe x,y,z których konsekwencją jest istnienie wektorów prędkości v (8) punktów, na płaszczyźnie prostopadłej do składowych wektora krętu (w naszym przypadku płaszczyzna YZ prostopadła do wektora krętu L_X). Wektory prędkości v (8) tworzą składowe (10) (L = r x p) wektora krętu(9).

    Aby jeszcze łatwiej było to zrozumieć interpretacja geometryczna wektorów prędkości (8)

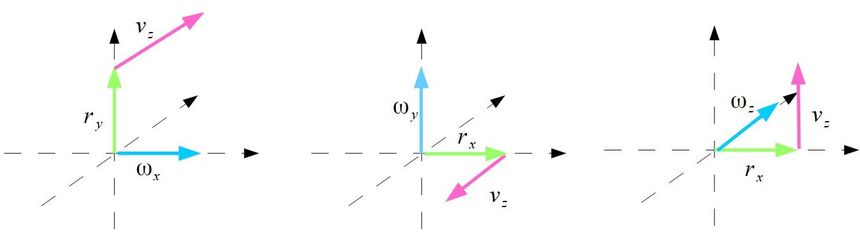
Zapewne kiedyś ktoś dokopie się do mojej pracy i zaczną mnie wyzywać od geniuszy aby usprawiedliwić obecne zaślepienie i ignorancje:)