W notce tej będą kalkulacje które już prezentowałem na swoim blogu, ale po ostatniej dyskusji widzę że niektóre rozwiązania wciąż budzą kontrowersje, a więc trzeba jeszcze raz to opisać. Rozwiązania nie są takie jak można by się spodziewać dlatego też wielu ma duże opory aby je zaakceptować.
Krótko od siebie. Znalezienie rozwiązań to jedno, ale przekonanie do nich Fizyków to istna katorga. Wszelkie próby wszczęcia dyskusji na ten temat kończą się słownymi przepychankami gdzie nie ma żadnych merytorycznych argumentów, żadnych kalkulacji a jedynie jakieś dziwaczne ogólniki które nic nie wnoszą, jak na jakimś targu albo w polskim sejmie, gdzie każdy rwie w swoją stronę ale już nikt nie pamięta o co ta awantura. Jest to bardzo destrukcyjne i niszczy mi głowę, skutecznie zniechęca do dalszego rozwijania tej wizji. Niby wszyscy wszystko wiedzą, niby jest to w podręcznikach, niby ja nic nie rozumiem a kiedy zadaje proste pytania nikt nie umie odpowiedzieć.
Pytanie było jak wyznaczyć wektory sił dla punktów tej bryły sztywnej
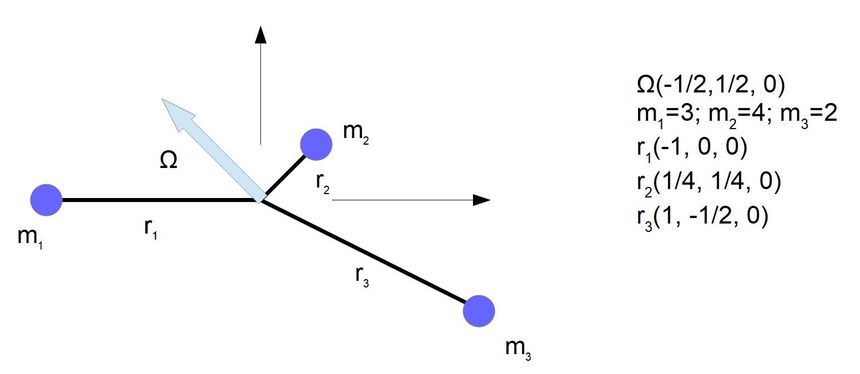
Aby wyznaczyć wektory sił dla punktów użyje podręcznikowego wzoru na przyspieszenie dośrodkowe
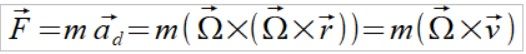 (1)
(1)
Po obliczeniach otrzymujemy następujące wektory sił
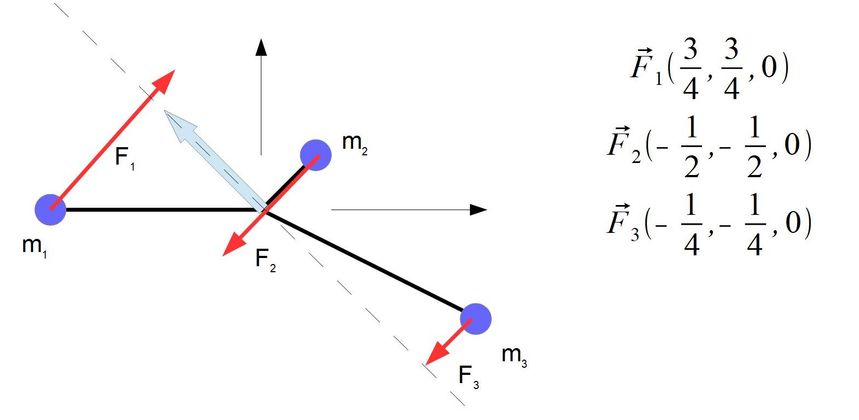
Suma tych wektorów jest zero, czyli zgodnie z oczekiwaniami środek ciała sztywnego nie ulega żadnym przyspieszeniom.
Dlaczego wektory te są doosiowe a nie centralne jak piszą w podręcznikach?
Aby odpowiedzieć na to pytanie musimy wiedzieć jak wyznaczać wektor siły gdy wektor położenia punktu nie jest prostopadły do wektora prędkości kątowej.
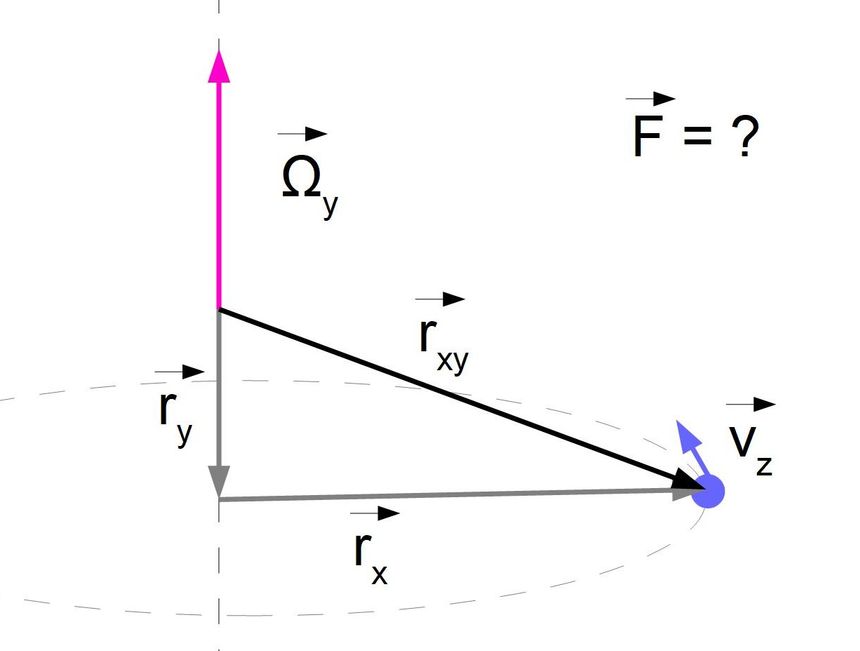
Bardzo długo brałem pod uwagę poprawność interpretacji podręcznikowych że siła ta jest siłą centralną i idzie wzdłuż ramienia. Czyli
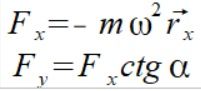
jednak wyliczając teraz prędkość kątową na podstawie tych sił dośrodkowych otrzymujemy
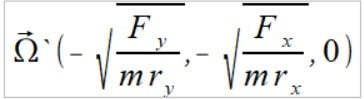
czyli prędkość kątowa uzyskana z tych sił jest inna niż pierwotna prędkość kątowa
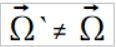
Próbowałem na wiele sposobów ale nie udawało mi się uzyskać zgodność wyników, aż nie zrozumiałem że istotą prędkości kątowej jest wzór (1). Punkt posiada swój wektor prędkości v na który działa wektor przyspieszenia (czyli tez siły) dośrodkowej a. Wektor prędkości kątowej Ω tworzy wektor prędkości v na który działa wektor przyspieszenia a i wektory te v, Ω i a muszą być zawsze do siebie prostopadłe.
Bardzo ciekawy jest też mechanizm działania prędkości kątowej na punkt. Punkt ma prędkość kątową prostopadłą do wektora położenia ale też prędkość kątową równoległą do wektora położenia, która obraca punktem wraz z jego wektorem prędkości v.
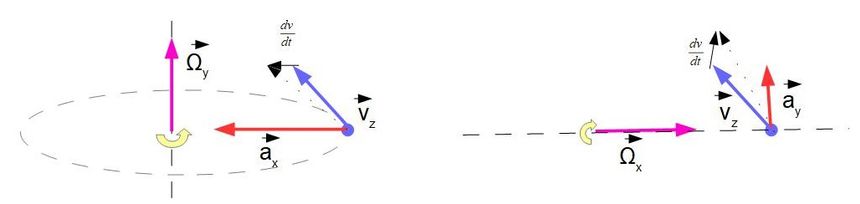
Sprawdzamy
m(rx, 0, 0)
Ω(ωx, ωy, 0)
używając (1) mamy
a=(-ω2y rx , -ω2y rx , 0)
licząc teraz prędkość kątową na podstawie naszego wektora przyspieszenia a otrzymujemy pełną zgodność
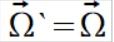
Z powodu braku czasu muszę na tym skończyć. W następnej notce o konsekwencjach jakie niesie za sobą ta interpretacja oraz pokazanie zgodności tej interpretacji z równaniami Eulera.
Dla Tadeusza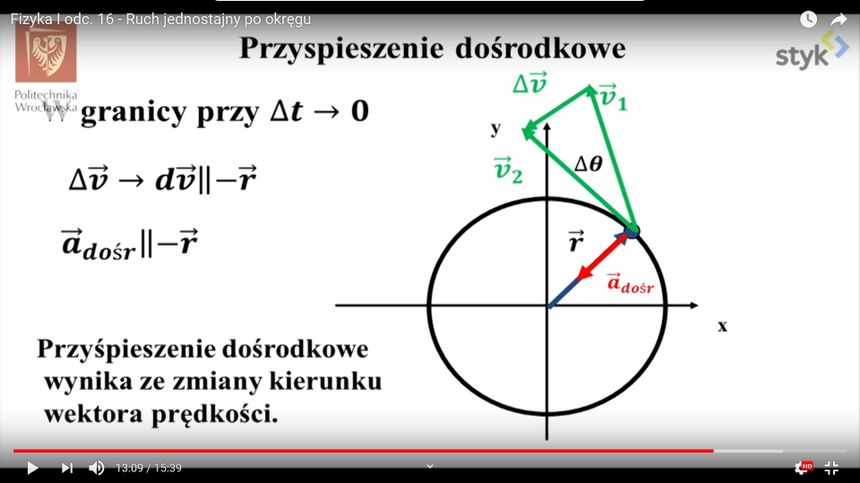
Inne tematy w dziale Technologie

