Dzisiaj policzymy energię i pęd dwóch rotujących wokół siebie czarnych dziur. Zakładam sobie model z miarę przystępnie okrągłymi liczbami, ale też, by z grubsza odpowiadał tym dziurom zaobserwowanymi przez LIGO.
Oto schemat:

oraz jego parametry:
Masy – każda z dwóch czarnych dziur ma masę 10 słońc.
Rodzaj orbity - kołowa.
Prędkość – v=1/3c = 100 000 km/s
Częstość kołowa - 50hz - z tego wynika promień orbity r= 318,31km, okres T=0,02s i prędkość kołowa ω=100pi
Zauważmy, że znaczna prędkość – 1/3 prędkości światła powoduje, że w przypadku gdy jedna z czarnych dziur będzie za drugą - grawitacja z tej tylnej czarnej dziury będzie na nas oddziaływać na tle przesuniętej pierwszej.
Dzielę okres obrotu na 16 części, by obliczyć przesunięcie czasowe faz i właściwą energię/ped widoczną przez nieruchomego obserwatora z zewnątrz dla każdej z faz osobno.
Przesunięcie faz można przedstawić przy pomocy schematu poniżej, gdzie linie pod kątem 45 stopni oznaczają prędkość światła.

Prędkość czarnych dziur względem obserwatora jest oznaczona falistą linią zawartą wewnątrz stożka światła. Ten schemat opracowałęm na podstawie podobnego diagramu Minkowskiego dostępnego w wikipedii: https://pl.wikipedia.org/wiki/Paradoks_bli%C5%BAni%C4%85t
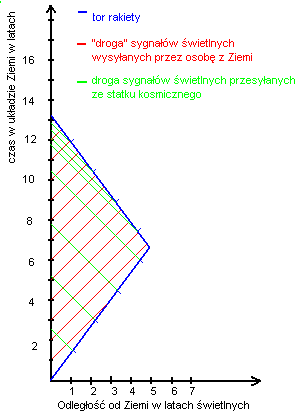
Wykreślając taki wykres – możemy wyznaczyć przesunięcia czasowe cyrklem i linijką.
Możemy też i obliczyć. W tym celu wystarczy zbudować proste równanie z niewiadomą tn , gdzie po jednej stronie mamy odległość jaką pokonała czarna dziura w kierunku obserwatora w czasie tn + czas jaki już minął od startu w pkt. 0 , a po drugiej drogę jaką pokonuje światło czasie tn :
r sin (ω *(tn+ (T/16 *n))= c tn które powtarzamy dla n od 1 do 16.
Przy okazji znając czas w którym zachodzi zdarzenie od 1 do 16 wyznaczamy kąty pomiędzy wektorem prędkości, a prostą łączącą z obserwatorem:
ϴ = ω *(tn+ T/16*n)

Z kątów możemy obliczyć relatywistyczny efekt dopplerowski wg wzoru z poprzedniej notki: fs/fo= γ(1+β cosϴ) . Mnożąc fs/fo przez masę spoczynkową uzyskamy łączną energię i pęd relatywistyczny.

Powyżej przedstawiam obliczone wyniki w formie wykresu masy relatywistycznej i pędu dla układu rotującego dwóch czarnych dziur o masach m=1. Mam wątpliwości czy całka z wykresów będzie właściwą wartością.
Podstawiając masę naszego słońca m=10ms uzyskany efekt będzie przez nas obserwowany jak znikająca i pojawiająca się grawitacja gwiazdy o masie około 2 słońc. Nie będzie on obserwowany w ustawieniu prostopadłym płaszczyzny obrotu do obserwatora. W następnej notce będzie o możliwości wykrywalności obliczonych fluktuacji pędu z odległości 1 mld lat świetlnych.
Inne tematy w dziale Technologie

