Czy poprawki relatywistyczne w systemie GPS wynikają z dylatacji czasu?

Teoria Względności zakłada szereg niezwykłości, które nadają jej szczególne miejsce w nauce. Przykładowo do realnych zjawisk fizycznych zalicza ona rozciąganie czasu i skracanie odległości, które wcześniej zarezerwowane były tylko dla... bajek. Jak łatwo się domyśleć nie od razu zaakceptowano taki obraz świata, ale pod naporem doskonałej zgodności TW z doświadczeniem oponenci musieli skapitulować.

Jeśli obecnie czasem jeszcze ktoś wyraża wątpliwości co do istnienia dylatacji czasu, to wtedy prawie zawsze pada argument dotyczący relatywistycznych poprawek w satelitach GPS. Chodzi o to, że satelity GPS nie mogą prawidłowo pracować bez uwzględnienia precyzyjnie wyliczonych przez TW poprawek czasowych wynikających z rozciągania czasoprzestrzeni.

Całkowita poprawka czasowa GPS wynika ze zjawisk:

- grawitacyjnych,

- relatywistycznych.

Zatrzymajmy się na tym drugim przypadku.

Zgodnie z STW wpływ zjawisk relatywistycznych powoduje, że sygnał GPS sterowany rezonatorem o okresie T₀ po dotarciu do ziemi ma inny okres T₁, stąd poprawka czasowa ∆t=T₁-T₀. Wynika ona wprost z dylatacji czasu wyrażanej współczynnikiem Lorentza γ dla ruchu satelity z prędkością v_L.

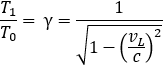
Ale my jesteśmy dociekliwi i chcemy wiedzieć skąd bierze się to bajkowe rozciągnięcie czasu? Przeanalizujmy zatem ruch przelatującego satelity. Załóżmy że satelita (w uproszczeniu) porusza się wzdłuż prostej x, a obserwator zadarł wzrok, żeby podziwiać zjawisko.

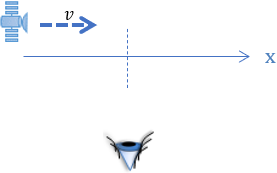
Niech proces mijania zaczyna się w momencie, gdy satelita znajduje się w punkcie –x₀, a kończy w momencie, gdy satelita znajduje się w punkcie x₀. Czyli początek i koniec sygnału są zlokalizowane w jednakowej odległość od obserwatora. Zobaczmy, jak wygląda to w układzie współrzędnych x, t. 

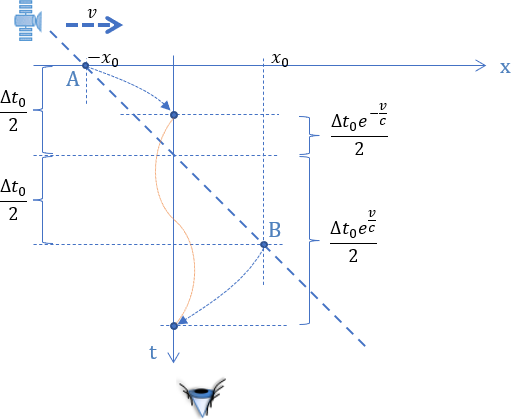
Oczywiście satelita nadal porusza się wzdłuż osi x, a pochylenie toru ruchu wynika tylko z dodania współrzędnej czasowej. Zależności na rysunku zostały wyprowadzone tutaj.

Punkty A i B to miejsca emisji odpowiednio początku i końca sygnału. Po lewej stronie rysunku zaznaczono okresy zegara satelity, a po prawej te same czasy rejestrowane przez obserwatora. Widzimy na tym wykresie, że grzbiety fal emitowane w odstępach czasu 1/2∆t₀, będą docierały do obserwatora w odstępach czasu odpowiednio 1/2∆t₀e^v/c i 1/2∆t₀e^-v/c. Możemy to zapisać poniższą zależnością.

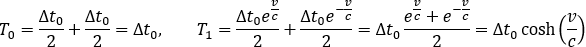
Jak widać sygnał docierający do obserwatora ma w naturalny sposób inny okres, niż wyemitowany przez satelitę. No i gdzie tu dylatacja czasu – nie ma. Toż to sama geometria. Dla formalności zapiszmy wynik w formie zgodnej z STW.

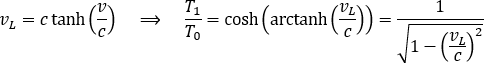
W efekcie za pomocą prostego rysunku i takichże obliczeń pokazaliśmy, że zmiana okresu emitowanego sygnału przez GPS jest całkowicie naturalną konsekwencją ruchu satelity i opiera się na klasycznej geometrii a nie wymyślnych czasoprzestrzennych niezwykłościach. Wystarczy tylko, że zaakceptujemy

- realną przestrzeń opartą na elastycznym ośrodku

- oraz wynikające stąd wzory Modelu Naturalnego,

aby wszystko stało się oczywiste i zwyczajne.

I tak oto uratowaliśmy zdrowy rozsądek w fizyce, a dylatacji czasu przywróciliśmy należne jej miejsce wśród rozwijających wyobraźnię baśniowych opowieści .