Dlaczego nie można obalić Teorii Względności? Najprościej mówiąc dlatego, że Teoria Względności daje prawidłowe wyniki. A prawidłowego wyniku nie można obalić. Skąd wiemy, że te wyniki są prawidłowe? Z tysięcy doświadczeń, które je potwierdzają i dowodzą poprawności wyliczeń.
Słowem obalacze nie mają szans. A potwierdzacze znajdą jeszcze jeden argument w tej notce. Dla zilustrowania zagadnienia zobaczmy, jak hipotetycznie mógłby wyglądać przykładowy dowód na nieprawdziwość Teorii Względności. Mamy plan taki: Porównamy dwie teorie (w tym STW), znajdziemy różnicę w obliczeniach, a potem za pomocą doświadczenia zweryfikujemy, który wynik jest prawdziwy.
To do dzieła. Analizę przeprowadzimy w kontekście następującego zadania:
Rakiety A i B mijają się w chwili t=0, a następnie w chwili t1=1h rakieta A wysyła sygnał laserowy w kierunku rakiety B. Sygnał odbija się od lustra w rakiecie B i wraca do rakiety A w chwili t2=4h. Pytanie brzmi, w jakiej chwili tS promień odbije się od lustra?
Zacznijmy od STW. Spojrzymy jak ta sytuacja wygląda w układzie odniesienia rakiety A.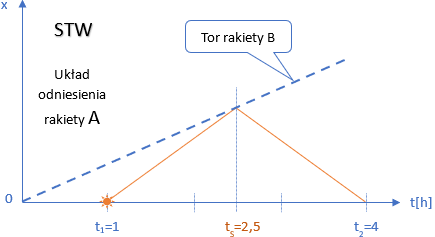
Przy założeniu, że promień porusza się z prędkością c rozwiązanie zadania jest natychmiastowe.
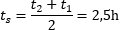
Możemy też obliczyć prędkość u, z jaką rakiety oddalają się od siebie.
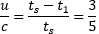
A teraz zobaczmy jak tę samą sytuacje opisuje druga teoria, niech to będzie Model Naturalny omawiany w poprzednich notkach.
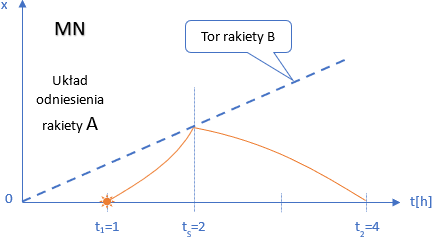
Tutaj (zgodnie z niniejszym wyprowadzeniem) szukaną wartość tS możemy wyliczyć z poniższych zależności.
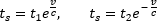
Powstaje układ dwóch równań, który po przemnożeniu stronami daje nam wynik.
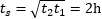
Jak widać otrzymany czas tS jest inny, niż w przypadku STW.
- zgodnie z STW uzyskaliśmy tS=2,5h
- zgodnie z MN mamy tS=2h
No to super, pierwsza część planu się udała – mamy różnicę w obliczeniach, o którą nam chodziło.
Teraz czas na doświadczenie rozstrzygające o tym, który wynik jest prawdziwy. Wykonujemy pomiar czasu tS w rakiecie B i otrzymujemy precyzyjną odpowiedź. Okazuje się, że sygnał dotarł do lustra dokładnie po czasie tS=2h. Czyli prawidłowe były wyliczenia Modelu Naturalnego. Ale zaraz… Czy to oznacza, że STW błędnie wyznaczyła ten czas? Ależ nie, przecież już mówiliśmy, że nie można obalić Teorii Względności. Wynik STW jest tak samo dokładny. Zobaczmy, jak to sprytnie zostało pomyślane. Einstein był geniuszem.
Pierwszy myk jest taki: Skoro czas zmierzony w rakiecie B okazał się inny, niż wyliczony w układzie rakiety A, to nie oznacza, że wynik jest błędny ale, że czas w obu rakietach biegnie inaczej. Zatem wystarczy przeskalować oś czasu i otrzymamy prawidłowy odczyt. Zobaczmy to na rysunku w układzie odniesienia rakiety B.
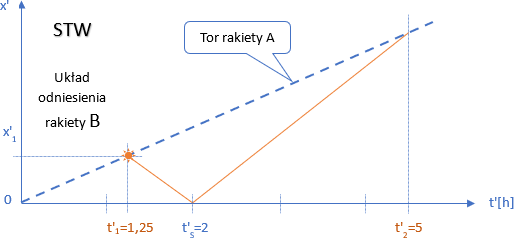
Dla odróżnienia nowe współrzędne zapisaliśmy w postaci primowalnej, ich wartości po przeskalowaniu t’1=1,25h i t’2=5h są tak dobrane, żeby otrzymać prawidłowy czas t’S=2h zgodny z doświadczeniem.
Poniżej są wyliczenia tych czasów, γ jest współczynnikiem Lorentza.
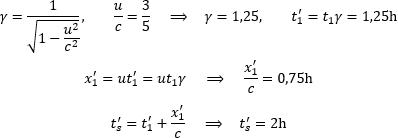
Jak widać, po korekcie wzory STW zwracają już prawidłowy czas t’S=2h zgodny z Modelem Naturalnym i potwierdzony eksperymentem.
Drugi myk jest równie pomysłowy: Skoro musieliśmy przeskalować współrzędne i one teraz nie pokrywają się z tymi w układzie własnym, to umawiamy się, że czas będziemy mierzyć wyłącznie w układzie własnym. Podkreślmy to wyraźnie – zgodnie z STW w każdym innym układzie tego czasu nie mierzymy.
A skoro nie mierzymy… O, to bardzo wygodne, ponieważ umożliwia takie jego umowne zdefiniowanie, żeby rachunki się zgadzały. Sprytne.
I właśnie dlatego nie można obalić Teorii Względności. Można jedynie wyjaśnić, dlaczego po wspomnianej korekcie zawsze otrzymamy dobry wynik. Dla jasności współrzędne, których nigdy nie mierzymy (a jedynie wyliczamy) zaznaczono na wykresach kolorem czerwonym.
Jeszcze na koniec wyjaśnienie, dlaczego w powyższych rozważaniach nie był nam potrzebny układ odniesienia rakiety B w Modelu Naturalnym. Otóż dlatego, że w tym układzie wszystkie czasy są takie same, jak w układzie odniesienia rakiety A. W MN wyniki są niezależne od układu odniesienia (bo w każdym istnieje ta sama chwila jednoczesności). Zobaczmy to dla formalności.
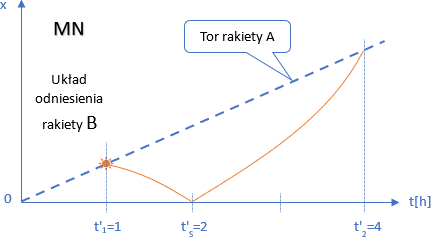
Rysunek przedstawia układ odniesienia rakiety B w MN. Współrzędne są zaznaczone na niebiesko, bo wszystkie możemy zmierzyć i doświadczalnie zweryfikować.
Inne tematy w dziale Technologie

