Eter nieruchomy, czy nawet wleczony został odrzucony doświadczalnie i nie ma co do tego wracać. Zostaje przestrzeń, którą zwykle rozumiemy jako próżnię czyli pustkę. Ale przecież próżnia ma swoje właściwości, choćby przenikalność elektryczną i magnetyczną, zatem jest to realny byt fizyczny a nie, jak zwykliśmy sądzić, po prostu nic. To dlaczego tę próżnię, czy cokolwiek wypełnia fizyczną przestrzeń, nie nazwać inną koncepcją eteru? Skoro propaguje tam fala EM, to jest to jakiś sprężysty ośrodek, który w dodatku pozwala pozbyć się paradoksów STW.
W poprzedniej notce, skąd głównie pochodzi powyższy lead, obiecaliśmy sprawdzić, jak omawiany model eteru tłumaczy zjawiska grawitacyjne. W tym, jak porusza się światło wewnątrz czarnej dziury, skąd wynika promień Schwarzschilda? I nie chodzi nam o „machanie rękami”, które zastępuje wzory i formuły. W naszych rozważaniach odwołujemy się ściśle do matematycznych wyprowadzeń i prezentujemy tylko to, co z nich wynika.
Nasz eter, to fizyczne punkty przestrzeni. Czym są te punkty? Łatwo to zobrazować przyrównując odcinek między dwiema drobinkami materii do nieskończenie rozciągliwej gumki, gdzie punkty przestrzeni to punkty na tej gumce.
Ale zanim korzystając z tej prostej definicji dojdziemy do matematycznego opisu toru fotonu poza horyzontem zdarzeń, musimy zacząć od pytania elementarnego. Jak pojedynczy punkt naszego eteru zachowa się w polu grawitacyjnym? Odpowiedź wymaga również elementarnego modelu układu pomiarowego.
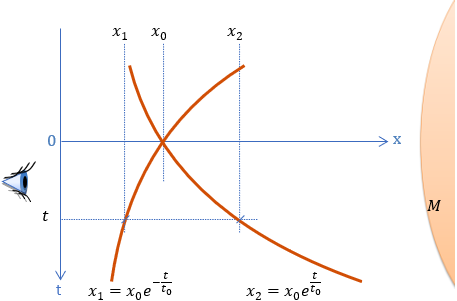
Zróbmy tak: Koniec naszego eteru-gumki umieśćmy przy powierzchni masy wytwarzającej grawitację, a drugi zaczepmy gdzieś daleko, poza zasięgiem sił przyciągania i właśnie z tego miejsca będziemy prowadzić obserwacje. Uzyskaliśmy sytuację (rysunek poniżej), w której odległy obserwator trzyma jeden koniec gumki, a drugi koniec spada sobie swobodnie w kierunku źródła grawitacji.
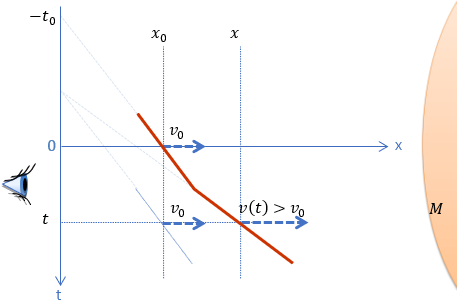
Zauważmy, że prędkość opadania gumki dla określonej współrzędnej x0 jest stała w czasie i zawsze równa v0. Natomiast koniec o współrzędnej x (czytaj dowolny fizyczny punkt przestrzeni) porusza się z narastającą prędkością v(t)>v0.
Literą M oznaczono masę, która jest źródłem grawitacji. Czerwoną linią zaznaczyliśmy tor opadania eteru dla dwóch wybranych współrzędnych czasowych oddalonych od siebie o t. Wykres ma postać łamanej, ponieważ został określony tylko dla dwóch współrzędnych na osi czasu.
Ale my szukamy nie łamanej, tylko dokładnego położenia x(t) w dowolnej chwili t. W tym celu skorzystajmy z następującej proporcji.
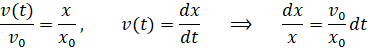
Aby obliczyć drogę opadania eteru x(t), należy rozwiązać poniższą całkę.
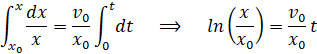
Po przekształceniu, otrzymamy szukaną postać wzoru na drogę eteru (lub pisząc bardziej obrazowo, na długość rozciąganej gumki).
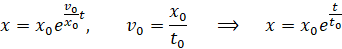
Powyższy wzór dotyczy warstwy rozciąganej eteru. Pamiętamy jednak z poprzedniej notki, że aby rozciągnąć jedną warstwę, drugą musimy ścisnąć. Drogę eteru w warstwie ściskanej obliczamy analogicznie, jak poprzednio. Zmienia się jedynie zwrot prędkości, co skutkuje minusem przed symbolem v0.
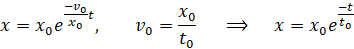
Nanieśmy tory ruchu obu warstw na jednym rysunku.
Uzyskane zależności stanowią wzory Modelu Naturalnego dla eteru przemieszczającego się swobodnie w polu grawitacyjnym:
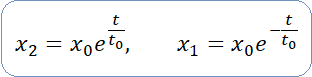
Zestawmy je z wzorami Modelu Naturalnego dla ruchu z prędkością v, które dobrze znamy w poprzednich rozdziałów:
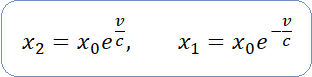
Co za uderzające podobieństwo, nieprawdaż? A przecież jedne dotyczą grawitacji, a drugie relatywistycznych prędkości. To nie może być przypadek, że wszystkie są jednakowo piękne i proste. Najwyraźniej natura w szczególny sposób upodobała sobie podstawę logarytmu naturalnego.
Wcześniejsze zależności (te z parametrem v/c) posłużyły nam do wyjaśnienia paradoksów Szczególnej Teorii Względności. Dodatkowo nowe wzory (te z parametrem t/t0) posłużą nam do opisu ruchu w polu grawitacyjnym. Zobaczymy, jak powstaje redshift grawitacyjny. Zrozumiemy, wyliczymy, narysujemy tor fali EM wyemitowanej także poza horyzontem zdarzeń i dlaczego wtedy nie jesteśmy w stanie zarejestrować jej w postaci docierającego fotonu.
Ale o tym już kolejnym razem.
Inne tematy w dziale Technologie

