Czy w kosmologii i relatywistyce potrzebujemy różnych definicji przestrzeni?

Na początek zagadnienie pomocnicze: Czy można przekroczyć prędkość światła? Oczywiście. W kosmologii jest to zjawisko powszechne i naturalne. Odległe galaktyki poruszają się względem nas znacznie szybciej, niż prędkość światła. Pojawia się pytanie, czy to nie narusza praw fizyki? Aby uratować Teorie Względności przyjęto, że to nie galaktyki się oddalają ale przestrzeń się rozszerza. Przez to relatywistyczne zależności pozostają nienaruszone, bo do takiej przestrzeni się nie odnoszą.

A zatem mamy już dwie przestrzenie, tę relatywistyczną i tę kosmologiczną. Czy faktycznie potrzebujemy obu, żeby opisać otaczający świat? Unifikacja w tym zakresie byłaby piękna, ale czy jest możliwa? Nie jesteśmy u Hitchcocka, to i napięcie nie musi narastać, dlatego powiem od razu, że tak, jedna wspólna definicja przestrzeni jest jak najbardziej możliwa, a przy tym jasno tłumaczy rejestrowane zjawiska.

Chodzi oczywiście o taką definicje przestrzeni, żeby wszystko się zgadzało z dotychczasową wiedzą zgromadzoną w obu dziedzinach, a przy okazji stało się logiczne bez paradoksów, żeby satelity działały jak dotąd, masa odpowiadała energii jak dotąd, a redshift odległych galaktyk w naturalny sposób wynikał z przyjętego modelu. Zaraz… Przecież mamy to już. Tą wspólną interpretację przestrzeni nazwaliśmy Modelem Naturalnym i szczegółowo omówiliśmy w poprzednich notkach:-)

No to skąd wiemy, że ta wspólna definicja przestrzeni jest zgodna z dotychczasową wiedzą zgromadzaną w kosmologii? To proste drogi Watsonie, bo tą wspólną przestrzenią jest właśnie przestrzeń kosmologiczna. Czyli zostaje do pokazania, że opisuje ona również zjawiska relatywistyczne, lepiej niż einsteinowska czasoprzestrzeń – bo bez paradoksów.

Zatem co można powiedzieć o fizyczności owej zunifikowanej przestrzeni? Jakkolwiek wydaje to się dość abstrakcyjne, spróbujmy zbudować model takiej przestrzeni, tej realnie występującej w przyrodzie.

Weźmy przestrzeń między dwiema ściankami pudełka i jakiś dowolny punkt tej przestrzeni. Co się stanie z tym punktem, gdy ścianki pudełka będziemy oddalać od siebie? Okazuje się, że odpowiedź na to pytanie nie jest oczywista.

W kosmologii przyjmuje się, że wspomniany punkt zachowuje się, jak rodzynek w rosnącym cieście. Przy takim ujęciu położenie dowolnego punktu przestrzeni jest zawsze jednoznacznie określone. Przykładowo punkt pośrodku pudełka zachowa swoje centralne położenie bez względu na to jak bardzo rozsuniemy ścianki i z której strony będziemy patrzeć. To jasne i nie wymaga rysunku.

W relatywistyce jest inaczej. Tutaj wszystko dzieje się względem jakiegoś obserwatora, układu odniesienia. Każdy punkt przestrzeni w układzie własnym obserwatora ma swoje stałe nieruchome położenie i nie oddala się wraz z rozsuwaniem ścianek. Tutaj przyda się rysunek.

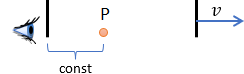
Odsuwanie ścianki z prędkością v nie wpływa na położenie wybranego punktu przestrzeni P w układzie własnym obserwatora. Analogiczną sytuację uzyskamy umieszczając obserwatora przy drugiej ściance.

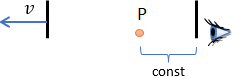
W efekcie ten sam punkt przestrzeni obaj obserwatorzy widzą niezmiennie w stałej odległości od siebie. Natychmiast pojawia się paradoks, jak to jest możliwe skoro ścianki (obserwatorzy) oddalają się? Widzimy, że przy takim ujęciu przestrzeni nie można określić położenia punktu P jednoznacznie, bo dla obu obserwatorów uzyskujemy sprzeczne wyniki. Możemy mówić jedynie o położeniu punktu w wybranym układzie odniesienia. Stąd nazwa Teoria Względności, bo wszystko można tu określić jedynie względem właśnie jakiegoś układu odniesienia.

W przypadku przestrzeni kosmologicznej nie ma takich problemów, tu wszystko jest jednoznaczne w czasie i możliwe do odtworzenia niejako w „zwolnionym tempie”. Pozwala to dokładnie prześledzić cały proces w 3D i obiektywnie pomierzyć odległości. W jaki sposób przestrzeń kosmologiczna pomaga realnie opisać zjawiska relatywistyczne, wynika wprost z naszych wcześniejszych wyprowadzeń. Jednak do tej pory wystarczyło nam podejście mechaniczne. Teraz z naszej wrodzonej ludzkiej ciekawości potrzebujemy wiedzieć coś więcej o fizyczności tej realnej przestrzeni?

Mówiąc o samej przestrzeni mamy zwykle ma myśli wypełniającą ją próżnię czyli pustkę. Ale przecież próżnia ma swoje właściwości, choćby przenikalność elektryczną i magnetyczną, czyli jest to realny byt fizyczny a nie, jak zwykliśmy sądzić, po prostu nic. To dlaczego tę próżnię, czy cokolwiek wypełnia tę przestrzeń, nie nazwać eterem? Skoro propaguje tam fala EM, to jest to jakiś sprężysty ośrodek.

No to zastanówmy się, jak musi być „zbudowana” ta przestrzeń, żeby możliwa była taka unifikacja zjawisk kosmologicznych i retatywistycznych. Przestrzeń składa się z punktów, nazwijmy je punktami swobodnymi. Jeśli w punkcie swobodnym umieścimy cząstkę, to na taką cząstkę nie działają żadne siły. Ale przestrzeń wypełniona eterem to nie tylko zbiór punktów, ona kipi życiem. Punt swobodny przestrzeni jest stanem równowagi procesów, które zachodzą w jego otoczeniu. Natomiast każda cząstka dąży do zajęcia miejsca w punkcie swobodnym przestrzeni, nieruchomo względem tego punktu.

W rzeczywistości eter wypełnia całą przestrzeń, a każdy element materialny jest zanurzony w eterze. Przejdźmy do konkretów i spróbujmy narysować model takiej przestrzeni o umownej grubości Δd, gdzie promieniująca cząstka spoczywa w punkcie swobodnym w odległości x₀ od jednej ze ścianek pudełka.

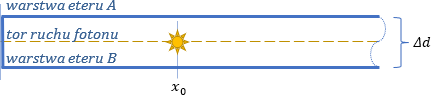
Zachodzi pytanie, jak możemy przemieścić cząstkę w tej przestrzeni za pomocą siły? Z poprzednich notek wiemy, że cząstki nie możemy dotknąć bezpośrednio, a jedynie możemy działać na eter, w którym cząstka jest zanurzona (bo każda cząstka to ostatecznie fala, a fale oddziałują poprzez sprężysty ośrodek, jakim jest eter). A zatem musimy rozciągnąć którąś warstwę tego eteru. Jednak, żeby to zrobić musimy mieć jakiś punkt podparcia. Co jest tym punktem? W świecie eteru, jedynym możliwym punktem podparcia jest tylko eter. Żeby jedną warstwę eteru rozciągnąć k razy, drugą warstwę musimy tyle samo razy ścisnąć.

W przyrodzie nie ma innej możliwości. Powiększmy nasz rysunek.

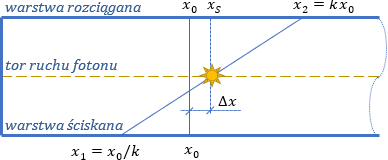
Zauważmy, że jeśli teraz warstwa rozciągana ma długość x₂ oraz warstwa ściskana ma długość x₁, to punkt swobodny przestrzeni przemieścił się o odcinek Δx, a tor ruchu fotonu uzyskał długość x_S.

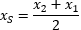
To uniwersalna zasada. Aby wyznaczyć drogę fali EM, należy obliczyć odległość, którą foton musiałby pokonać biegnąc po warstwie rozciąganej x₂ oraz drogę, która musiałby pokonać biegnąc po warstwie ściskanej x₁, dopiero wtedy możemy wyliczyć wartość x_S.

Analogicznie uzyskujemy czas podróży fotonu t_S. Gdyby fala EM poruszała się po warstwie rozciąganej, to dotarłaby do brzegu po czasie t₂. Gdyby biegła po warstwie ściskanej, to dotarłaby do brzegu po czasie t₁. Ale fala propaguje środkiem wzdłuż linii nazwanej „tor ruchu fotonu”, dlatego dotrze do celu po czasie t_S, zgodnie z poniższym wzorem.

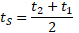
Pamiętamy ile wynoszą odległości x₁ i x₂ w przypadku rozciągania eteru ze stała prędkością v.

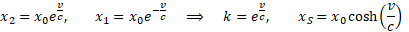
I jak powyższe zależności tłumaczą zjawiska relatywistyczne, np. efekt Dopplera, pęd, masę, czy energię kinetyczną. Przypomnijmy końcowe formuły opisujące dwa dwa ostatnie z tych pojęć:

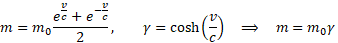
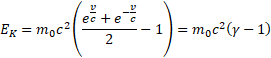
Gdzie γ w tych wzorach jest współczynnikiem Lorentza. Jak widać odwołanie się do przestrzeni kosmologicznej daje wyniki spójne ze wzorami Einsteina. W dodatku bez paradoksów, bo zamiast Transformacji Lorentza mamy tu zwykłą geometrię klasyczną, no i składanie prędkości odzyskuje wreszcie swoją naturalną postać v₃=v₁+v₂.

Akceptując istnienie eteru w tej zunifikowanej przestrzeni, mogliśmy „klatka po klatce” prześledzić cały proces ruchu, a także jednoznacznie i bez magii wskazać obiektywne położenie relatywistycznej cząstki w dowolnej chwili.

W kolejnych notkach sprawdzimy, jak niniejsza właściwość eteru oraz powyższe wzory tłumaczą zjawiska grawitacyjne. Zajrzymy do wnętrza czarnej dziury. Pokażemy, jak zrozumiałe są zachodzące tam procesy kiedy wynikają z prezentowanego modelu. A mając jasny obraz zjawiska, znajdziemy matematyczny opis toru fotonu także poza horyzontem zdarzeń. Wyliczymy i wykreślimy każdy etap podróży fali EM w polu grawitacyjnym precyzyjnie, jak wcześniej przy zależnościach relatywistycznych „klatka po klatce” i wreszcie wyjaśnimy (a wręcz zobaczymy) skąd wynika promień Schwarzschilda R_S. Odkryjemy jak zachowuje się światło, gdy masa ma promień mniejszy niż R_S, no i dlaczego to takie oczywiste i logiczne.