Ze zjawiskiem aberracji światła wiąże się fascynująca niezwykłość polegająca na tym, że aby zaobserwować gwiazdę za pomocą teleskopu – musimy skierować go w inne miejsce nieba odchylając o kąt θ od linii wyznaczającej położenie gwiazdy.
Link do poprzedniej notki
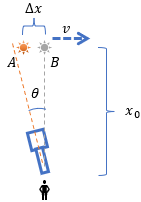
Zakładając, że gwiazda znajduje się dokładnie nad naszą głową w punkcie B, aberrację światła (aberrację gwiezdną) możemy zobrazować za pomocą poniższego rysunku.
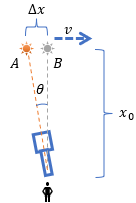
Zjawisko odkrył J. Bradley i wyliczył kąt θ porównując prędkość światła z prędkością Ziemi. W swoich obliczeniach uwzględnił fakt, że rejestrowany sygnał pochodzi z przeszłości, gdy gwiazda względem obserwatora znajdowała się jeszcze w punkcie A odległym o Δx od punktu B.
Drogę Δx łatwo wyliczymy znając odległość do gwiazdy x0 i prędkość gwiazdy względem obserwatora v. (Podkreślmy, że mówimy o prędkości względnej.)
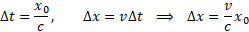
Stąd otrzymujemy kąt θ wyliczony przez Bradleya.
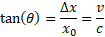
Wszystko zrozumiałe i jasno przedstawione na rysunku. Niestety problem w tym, że uzyskany w ten sposób kąt θ jest nieprawdziwy. Pojawiła się Teoria Względności i okazało się, że w rzeczywistości kąt θ jest większy od wyliczonego przez Bradleya, a jego dokładna wartość wynosi:
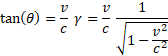
A zatem prawidłowy wynik różni się od poprzedniego współczynnikiem Lorentza γ.
Ktoś jednak w tym momencie może zadać zaskakujące pytanie: Ale jak teraz biegnie ten promień światła? Przecież droga Δx nie zmieniła się bo jasno wynika z prędkości światła c i znanej odległości x0 do gwiazdy. No i jeszcze z prędkości v, która też jest stała.
A tymczasem nowe pochylenie teleskopu powoduje, że teraz jego oś nie trafia w punkt A.
Jak logicznie wytłumaczyć, że obserwator pod tym katem widzi gwiazdę?
Całe zjawisko staje się zrozumiałe, jeśli narysujemy sobie, jak rozchodzi się fala EM.
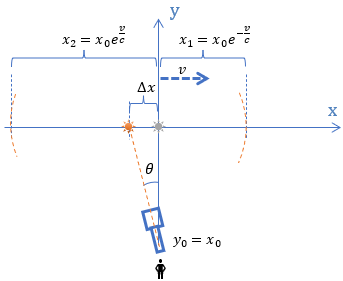
Ze wzorów Modelu Naturalnego wiemy, że jeśli długość emitowanej fali wynosi x0, to wtedy jej grzbiety propagują w odstępach x1 oraz x2. Obliczmy zatem nasz kąt θ, pod którym fala dociera do obserwatora.
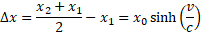
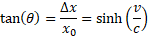
I oto chodziło. Otrzymaliśmy szukany wzór, który określa kąt aberracji. Zależność w jasny sposób wynika z powyższego rysunku i tłumaczy istotę zjawiska.
Ten sam wzór wyrażony za pomocą prędkości Lorentza vL przybierze przytoczoną na początku dobrze znaną postać:
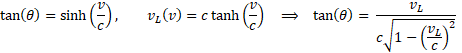
Tak właśnie należy ten wzór poprawnie zapisać, jako zależność od vL (gdzie vL jest funkcją rzeczywistej prędkości v, z jaką porusza się gwiazda względem obserwatora).
Inne tematy w dziale Technologie

