Rapidity w Transformacji Lorentza

Część #1: Teoria opisująca ruch obiektów poruszających się z dowolnymi prędkościami
Część #2: Mrówka relatywistyczna
Część #3: Prędkość Lorentza
Część #4: Szybciej, niż światło – wyprowadzenie formuły ruchu

Część #5: Rapidity w Transformacji Lorentza 

Zacznijmy od pytania z poprzedniej notki: Czy foton dogoni cel oddalający się z prędkością v większą od światła?

Odpowiedź wynika bezpośrednio ze wzorów Modelu Naturalnego.

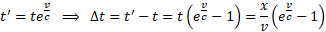
Przykład:

• Prędkość v=3c,
• Początkowa odległość x=1 sekunda świetlna.

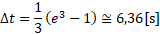
A zatem odpowiedź brzmi: Tak, foton dogoni trzykrotnie szybszy odbiornik z przykładu w czasie zaledwie kilku sekund. A dodatkowo uderzy w niego z prędkością c. 

Związek między prędkościami w Modelu Naturalnym i Teorii Względności.

Jak pamiętamy, prędkość w Transformacji Lorentza zdefiniowana jest następująca zależnością:

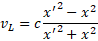
Natomiast prędkość w Modelu Naturalnym określona jest poniższym wzorem: 

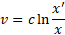
Pozwala to związać obie wielkości jedną formułą:

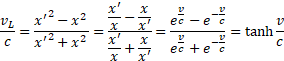
A zatem prędkość Lorentza v_L okazała się funkcją prędkości v. Czy coś nam ten wzór przypomina? Tak, wyrażenie v/c=φ jest znane, jako rapidity czyli pewien kąt hiperboliczny φ=atanh(v_L/c), który zdecydowanie uprasza obliczenia związane z Transformacją Lorentza. Współczynnik 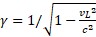, to po prostu γ=cosh(φ), a dodawanie prędkości  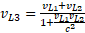zastąpione zostaje przez proste φ₃=φ₁+φ₂. 

Co to oznacza? To oznacza, że wszelkie zależności wyprowadzone na podstawie Modelu Naturalnego i dotyczące prędkości v, automatycznie tłumaczą się na dobrze znane i powszechnie używane rapidity. Gwarantuje to spójny opis zjawisk dokonany na podstawie naszego modelu i Szczególnej Teorii Względności.

To po co jest Model Naturalny i co on zmienia? Można by powiedzieć, że nic. Gdyby nie to, że Model Naturalny gruntownie odwraca znaczenie pojęć w zależności 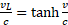, zmieniając ich interpretację. Dotąd za prawdziwą prędkość było uznawane v_L (właśnie stąd wzięło się tak dziwne dodawanie tych wielkości), Model Naturalny (na podstawie przyjętego postulatu) dowodzi jednak, że prawdziwą prędkością w przyrodzie jest v. Taki model ruchu nie potrzebuje do opisu skracania odcinków, wydłużania czasu, wystarczy mu zwykła geometria i klasyczne zależności. A skoro cały proces jest tak zrozumiały, intuicyjny i prosty, jak ruch mrówki po rozciąganej gumce… Można przypuszczać, że gdyby w czasach Einsteina znany był Model Naturalny, nikt by nie próbował tłumaczyć zjawiska ruchu za pomocą Transformacji Lorentza.

Wyjaśnienie efektu Dopplera dla światła

Skoro geometryczny aspekt ruchu fotonu umiemy opisać tymi samymi wzorami, co drogę mrówki (ściślej grupy mrówek, bo jedna mrówka to pojedynczy grzbiet fali) – sformułujmy następujące pytanie: Jeśli mrówki będą startować z jednego brzegu gumki z częstotliwością f₀, to z jaką częstotliwością dotrą na drugi brzeg?

Dla przypadku, gdy końce gumki oddalają się, napiszemy:

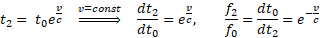
Jeśli brzegi przybliżają się, uzyskamy analogiczną zależność 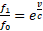. Oba wzory opisują Efekt Dopplera w Modelu Naturalnym.

Aby zobrazować, jak bardzo zwyczajne jest to zjawisko, zilustrujmy je rysunkiem.

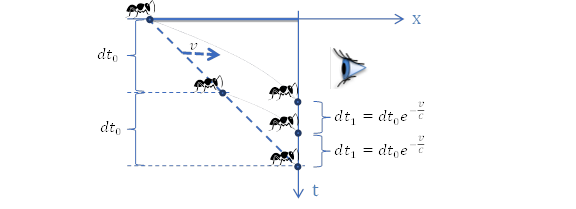
Obserwacje prowadzimy z jednego brzegu gumki, a drugi zbliża się z prędkością v. Zgodnie z uzyskanym wzorem mrówki startujące w odstępach czasu dt₀ dobiegną do obserwatora w odstępach czasu .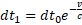

Analogicznie wygląda rysunek dla oddalającego się brzegu gumki.

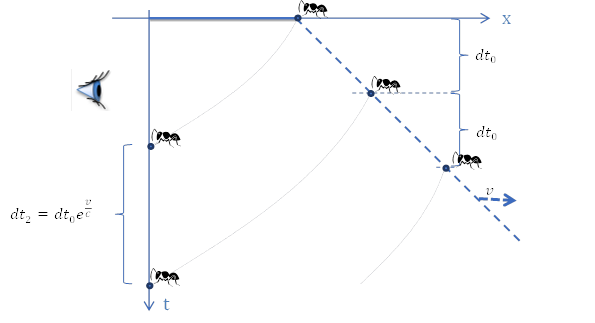
Mrówki startujące w odstępach czasu dt₀ dobiegną do obserwatora w odstępach czasu .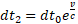
Porównajmy Efekt Dopplera w Modelu Naturalnym dla zbliżającego się końca gumki 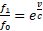 z relatywistycznym Efektem Dopplera danym wzorem  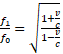dla tego samego przypadku. Skąd ta różnica w obu zapisach? Wszystko staje się jasne, gdy uświadomimy sobie, że w relatywistycznym wzorze nie występuje prędkość v ale funkcja v_L(v), która jak pamiętamy z wcześniejszej części została "skorygowana". A to prowadzi już bezpośrednio do wzoru w Modelu Naturalnym.

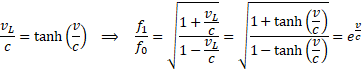
Jak widzimy, obie formuły definiujące Efekt Dopplera są równoważne. 

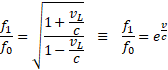
Musimy tylko pamiętać, że we wzorze relatywistycznym nie występuje prędkość v, ale funkcja v_L(v), w której prędkość v jest jedynie parametrem.

Trochę się rozgadałem… Nie chcę, żeby automat dzielił notkę. O przyroście masy, pędzie i energii będzie następnym razem.

Część #6: Relatywistyczny przyrost masy, pędu i energii