Opracowanie prezentuje model eteru zgodny z doświadczeniem Michelsona-Morleya oraz wyprowadza równania ruchu dla prędkości ponadświetlnych.
Część #1: https://www.salon24.pl/u/model-naturalny/678523,bedzie-sie-dzialo
Część #2: https://www.salon24.pl/u/model-naturalny/1186931,mrówka-relatywistyczna
Część #3: https://www.salon24.pl/u/model-naturalny/1187226,predkość-lorentza
(4) Model Naturalny
Wyprowadzenie formuły ruchu dla obiektów poruszających się z dowolnymi prędkościami
Mając do czynienia się z nieznanym, jakim jest natura fotonu gotowi jesteśmy przypisać mu magiczne właściwości. Jednak nie odmawiając zagadkowości tej tajemniczej formie energii nasze rozważania dowodzą, że ruch fotonu można opisać w klasyczny sposób, jeśli spełniony jest następujący postulat:
Foton porusza się miedzy nadajnikiem a odbiornikiem w ośrodku rozpiętym na wzór nieskończenie rozciągliwej i nieważkiej gumki. Możemy ten ośrodek nazwać eterem, próżnią albo ze względu na jego nieważkość właściwością przestrzeni.
Tak zdefiniowany eter jest zgodny z doświadczeniem Michelsona-Morleya oraz pozwala wszystkie obliczenia przeprowadzić w geometrii euklidesowej bez czwartego wymiaru i wręcz automatycznie wyjaśnia paradoksy związane z Teorią Względności.
W naszych obliczeniach występuje jeden zegar i wspólna chwila jednoczesności. Z tego też powodu nie ma potrzeby skracania odcinków, czy wydłużania czasu, a prędkość może przyjmować dowolne wartości aż do nieskończoności.
Uspokajam, że uwzględniając niniejszy model ruchu nadal będą potrzebne poprawki czasu w satelitach GPS, nasza teoria nie zmienia natury, tylko ją wyjaśnia.
Wyprowadźmy zatem formułę ruchu dla modelu zgodnego z zaprezentowanym postulatem. Dla zgodności z przyjętą konwencją foton będziemy wizualizować za pomocą zupełnie nietajemniczej mrówki, natomiast eterem będzie rozciągana gumka.
 Rysunek 4.1
Rysunek 4.1
Na rysunku przedstawiono podróż naszej mrówki (fotonu) w kierunku odbiornika oddalającego się z prędkością v. Zauważmy, że jej prędkość względem oka w chwili t wynosi c+u(t), ponieważ musimy uwzględnić prędkość „unoszenia” u(t) mrówki przez gumkę. A zatem prędkość mrówki względem obserwatora jest większa od c o prędkość u(t). Wyliczmy tę prędkość.
Prędkość unoszenia jest tym większą, im dalej od oka znajduje się mrówka. Jej chwilową pozycję oznaczyliśmy jako x(t). Jak widać, gdy mrówka jest w punkcie obserwacji x(t)=0, jej prędkość unoszenia równa jest zeru u(t)=0. To wyjaśnia tajemnicę stałej prędkości c.
Zapamiętajmy: Pomiar prędkości mrówki, dokonany w miejscu obserwacji, zawsze da wynik równy c, niezależnie od prędkości rozciągania gumki v.
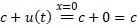
Logiczną konsekwencją tej zależności jest wbudowana w opisywane zjawisko następująca nieoznaczoność. Nie jesteśmy w stanie zaobserwować rzeczywistej prędkości fotonu (mrówki) podczas ruchu, ponieważ każda ingerencja pomiarowa zakłóca układ i przesuwa brzeg gumki w to miejsce, które badamy. Wniosek – nie umiemy zarejestrować innej prędkości mrówki niż c.
Nawet jeśli wiemy, że w punkcie x prędkość fotonu względem obserwatora wynosi c+u, to próba zmierzenia prędkości w tym punkcie da zawsze wynik c. Bez zrozumienia tego mechanizmu i opierając się tylko na dokonanych pomiarach, łatwo o wniosek, że foton porusza się z prędkością c względem wszystkiego jednocześnie.
Ale przejdźmy do pytania, które możemy sformułować tak: Jak porusza się foton biegnąc w kierunku ruchomego odbiornika? Albo jak naprawdę przemieszcza się nasz kwant światła wyemitowany z nadajnika oddalającego się z prędkością v?
W tym celu wróćmy do naszego modelu z mrówką w roli fotonu i wyprowadźmy wzory opisujące jej parametry ruchu. Obliczenia bardzo się uproszczają, jeśli posłużymy się poniższymi rysunkami. Drogę mrówki wykreśliliśmy we współrzędnych (x, t), żeby dokładnie prześledzić cały proces.
Oto tor ruchu mrówki obserwowany z lewej strony:
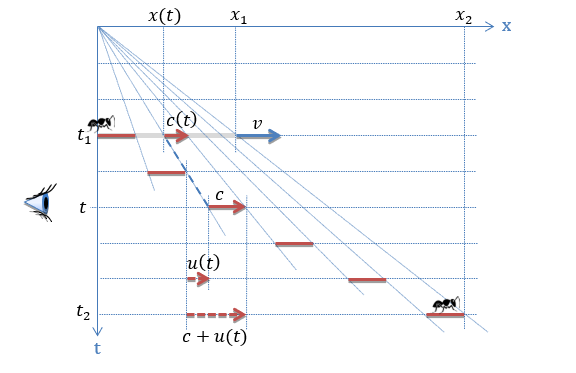 Rysunek 4.2
Rysunek 4.2
Ta sama sytuacja oglądana z prawej strony:
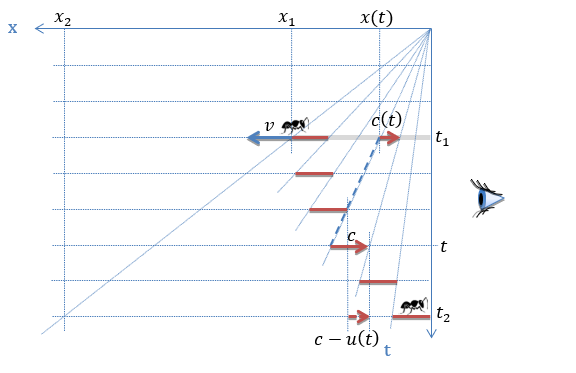 Rysunek 4.3
Rysunek 4.3
Opis:
- Gumkę (szara linia) rozciągamy z prędkością v.
- Czerwone odcinki, to droga mrówki w kolejnych jednostkach czasu.
- Mrówka startuje w chwili t1, gdy gumka ma długość x1.
- Mrówka dotrze na drugi brzeg w chwili t2, gdy gumka będzie miała długość x2.
- Wyrażenie u(t) oznacza chwilową prędkość unoszenia mrówki przez gumkę.
Dla lepszej wizualizacji, prędkości na rysunku są odniesione do pewnego czasu dt i naniesione na oś x, jako odcinki.
Zauważmy, że chwilowa prędkość mrówki względem obserwatora na rysunku 4.2 wyraża się zależnością c + u(t), natomiast na rysunku 4.3 funkcją c - u(t). Jednak, gdy zrzutujemy końcową długość gumki x2 na początkową x1, to w obu przypadkach możemy wyrugować z obliczeń funkcję u(t) i prędkość chwilową mrówki zapisać tym samym wyrażeniem c(t). Zobaczmy to w obliczeniach.
W nieskończenie krótkiej chwili dt mrówka pokona zrzutowaną drogę dx. Suma przebytych odcinków dx w czasie od chwili t1 do chwili t2 jest równa odległości x1. Możemy zapisać to w postaci całki:
Ostatecznie otrzymujemy:
Oto formuła ruchu dla obiektów poruszających się z dowolnymi prędkościami. Prosta, prawda? Dla zgodności oznaczeń z Transformacją Lorentza, zmieńmy symbole t2, x2 na wielkości primowalne oraz t1, x1 na nieprimowalne, wtedy możemy ją zapisać w postaci następujących równań.
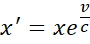 (4.1)
(4.1)
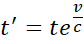 (4.2)
(4.2)
Definiują one zależności czasu i przestrzeni dla naturalnego modelu ruchu opartego na rzeczywistej prędkości rozciągania gumki v, nazwijmy go krócej Modelem Naturalnym. Zauważmy, że uzyskane wzory nie nakładają żadnych ograniczeń na prędkość v, która może być dowolnie większa od c.
W Modelu Naturalnym nie potrzebujemy też współczynnika dopasowującego obserwacje dokonane jednym okiem i drugim okiem (poprzez kontrakcje odcinka i dylatację czasu), bo nasz wynik jest taki sam dla obu przypadków.
Na marginesie zauważmy, że dla małych prędkości v wzory Modelu Naturalnego można wyrazić za pomocą Transformacji Lorentza. Spójrzmy na rozwinięcie funkcji ekspotencjalnej w szereg.
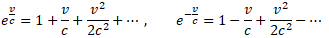
Pomijając dla małych prędkości v elementy rozwinięcia drugiego i wyższych rzędów oraz uwzględniając, że wtedy czas podróży mrówki możemy uznać za równy t=x/c, uzyskujemy dobrze znany wzór.
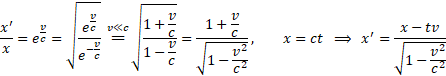
W odniesieniu do Modelu Naturalnego powiemy, że jeśli początkowe położenie cząstki poruszającej się z prędkością v było x, to w chwili t, gdy informacja o tym dotrze do obserwatora, cząstka będzie znajdowała się w położeniu x'.
A teraz pytanie: Czy mrówka dogoni trzykrotnie szybszy koniec gumki? Czy foton dogoni odbiornik oddalający się z prędkością większą od światła?
W następnej notce o tym, jak Model Naturalny pozwala wyliczyć masę, energię, pęd cząstki oraz dlaczego każde zjawisko opisane za pomocą Transformacji Lorentza automatycznie znajduje wyjaśnienie w Modelu Naturalnym bez odwoływania się do względności czasu.
Część #5: Rapidity w Transformacji Lorentza
Inne tematy w dziale Technologie

