Podaj fakty znane fizykom, chemikom, elektrotechnikom...

Technologie, Badania i rozwój

Sztuka to fizyka bez matematyki

Start-up: "inżynieria hydroelektronowa":
Jak myśleć w idei materialnymi elektronami swobodnymi i cząsteczkami wody?
Rzecz: przedmiot materialny, elektron cząstka materii, H₂O cząsteczka materii.
Jak obliczyć ile elektronów swobodnych można zgromadzić w zbiorniku z wodą?
Wirtualna konfrontacja idei hydroelektronowej w naturze ułożeń niemożliwych.

*

Inspiracja: "SNAFU niczego nie odkrył, tylko podał kilka faktów dobrze już fizykom znanych. Serdeczne pozdrowienia!" (link)

Chodzi o fakty związane z pomysłem na uzyskanie względnego wzrostu pojemności elektrycznej o milion razy w przypadku spełnienia podanych uwarunkowań, o których napisał SNAFU pod notka pt. "Fizyka rzeczy niemożliwych".

*

Zatem szkic ułożenia w postaci rysunku w labiryncie idei hydroelektronowej:

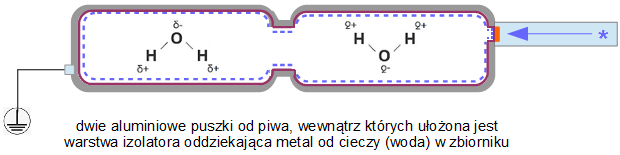
spojrzenie → na ułożenie idei w rysunku → jakie znane fakty w nauce i technice zawiera obraz?

Oczywiście można zapytać znajomego fizyka, chemika, elektrotechnika...

Co w rysunkach jest prawdą nauki lub fantastyką albo może ups-żartem?

"Fantastyka – gatunek literacki, a także filmowy, komiksowy, gier a niekiedy i malarstwa. Polega ona na kreowaniu świata przedstawionego, który w całości, lub w części różni się od rzeczywistości, na przykład przez dodanie elementów nadnaturalnych, lub stworzonej przez autora technologii" - link.

Można by na rysunku dodać wybrane znane fakty nauki, których w powyższych obrazach nie ma.

Jeżeli ładunek elektryczny w postaci wprowadzonych do zbiornika elektronów za pomocą działa elektronowego uda się utrzymać na wewnętrznej powierzchni zbiornika zamkniętego, to fakty znane fizykom będą spełnione dla naelektryzowania zamkniętej powierzchni wewnętrznej. I więcej, wykonanie zbiornika w postaci z idei metody SNAFU sprawi, że względny "wzrost pojemności może być rzędu MILIONA razy!" Zatem sukces eksperymentu potwierdzającego efekt prawie pewny, ponieważ zależy od umiejętności w zakresie inżynierii materiałowej i konstrukcji układu czyniącego udane pozostawienie na wewnętrznej powierzchni elektronów, czyli zależy od kosztów, pieniędzy.

Ułożenie:

wybór znanych faktów → hipoteza względem układu hydroelektronowego → sukces projektu technicznego

Więcej znanych faktów!

*
Dopisane 29-31.03.2024 r.

1. Ładunek cząstkowy:

δ(+) H₂O δ(-), ładunek cząstkowy dodatni 2 × +0,38 e, ujemny -0,76 e
δ(+) H₂O δ(-), ładunek cząstkowy H od +0,3 do +0,4, O od -0,6 do -0,8
3 * [ δ(+) H₂O] = 3 * δ(+0,3 ~ +0,4) = δ(+0,9 ~ +1,2) → w idei śred. 1,1

Elementarny ładunek elektryczny | e- | = 1,602 176 634 × 10^-19 C

W cząsteczce H₂O środek ładunku dodatniego, będący w połowie odległości między dwoma atomami wodoru, nie pokrywa się ze środkiem ładunku ujemnego na atomie tlenu w wyniku czego powstaje molekularny elektryczny moment dipolowy (link), moment dipolowy cząsteczki H₂O i skierowany jest od środka ładunku ujemnego do środka ładunku dodatniego. Wypadkowy moment dipolowy H₂O wynosi p = 6,15 × 10^-30 C · m. Moment dipolowy cząsteczki wody powoduje jej polarny charakter.

Wektor elektrycznego momentu dipolowego ma kierunek prostej łączącej ładunki i zwrot od ładunku ujemnego do dodatniego.

Dla momentu dipolowego H₂O, moment dipolowy równoważny jest jednostkowemu ładunkowi ujemnemu (jednemu elektronowi) oddzielonemu od jednostkowego ładunku dodatniego o 0,061 nm.

V_H2O - objętość cząsteczki wody ok. 0,03 nm³.
D_H2O - średnica cząsteczki wody ok. 0,27 nm.
1 nanometr równa się 10⁻⁹ m.

pole powierzchni zbiornika (S_Z) = k * objętość zbiornika (V_Z), k = S_Z / V_Z
S_G (Gaussa) = S_Z (zbiornika)

2. Obiekty w idei domeny elektrostatycznej obejmującej zbiornik i jego otoczenie:
"woda w zbiorniku" → izolator → metal puszki → otoczenie [ (→ uziemienie: ziemia, potencjał V = 0); powietrze; inne obiekt ]

3. Sfery w idei domeny elektrostatycznej:

sfera dipolowa - sfera dipoli H₂O stanowiąca powierzchnię wody w zbiorniku o średnicy H₂O

objętość dipolowa H₂O - część objętości zbiornika przy jego wewnętrznej powierzchni równa iloczynowi powierzchni zbiornika (wody) i średnicy H₂O

sfera elektronowa - sfera naelektryzowania elektronami swobodnymi wprowadzonymi z działa elektronowego w założeniu, że po wprowadzeniu elektronów lokują się pomiędzy powierzchnią wody i izolatorem.

4. Umowne rozmiary puszki (walca):

V = 1 dm³
h = 33,6 cm
r = 3,1 cm
S = 709,3 cm², pole powierzchni walca
Sp = 29,8 cm², pole podstawy
Sb = 649,8 cm², pole powierzchni bocznej
Grubość ścianki puszki dp = 0.097 mm
k = S_Z / V_Z, k = 709,3 * 0,01 dm² / 1 dm³, k =  7,093 / dm
1 cm² = 0,01 dm²

5. Ilość cząsteczek wody w objętości dipolowej H₂O:
N_H2O = V_d / V_H2O
V_d = S_Z *  D_H2O
1 nanometr = 1,0 × 10^-7 centymetra
V_d = 709,3 cm² * 0,27 nm
V_d = 709,3 cm² * 0,27 × 10^-7 cm
V_d = 191,5 × 10^-7 cm³
N_H2O = 191,5 × 10^-7 cm³ /  0,03 nm³
N_H2O = 191,5  × 10^-7 cm³ /  0,03 × 10^-21cm³
N_H2O = ~6383,33 × 10¹⁴ = ~6,4 × 10¹⁷
N_H2O = ~6,4 × 10¹⁷

6. Ilość dipoli H₂O zwróconych ładunkiem dodatnim w stronę sfery elektronowej (N_d):

6.1. N_d = N_H2O / 2, czyli połowa cząsteczek H₂O w sferze dipolowej z wektorem p skierowanym w stronę sfery elektronowej, a połowa skierowanym w stronę przeciwną

N_d = ~6,4 × 10¹⁷ / 2 = ~3 × 10¹⁷

6.2. Cztery ułożenia H₂O w idei statystyczno-termodynamicznej względem sfery elektronowej:

Rysunek 1.

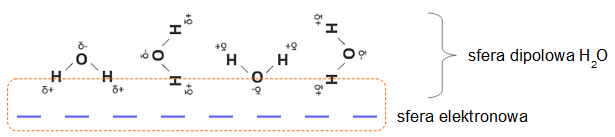
N_d = N_H2O / 4
N_d = ~6,4 × 10¹⁷ / 4 = ~1,6 × 10¹⁷ → jeden dipol H₂O zwrócony bezpośrednio w stronę sfery elektronowej.

Moment dipolowy równoważny molekularnemu elektrycznemu momentowi dipolowemu H₂O ładunkiem dodatnim "neutralizuje" w sferze elektronowej wpływ jednego elektronu swobodnego wprowadzonego do zbiornika.

N_d → 10¹⁷ elektronów swobodnych wprowadzonych do zbiornika związanych z dipolami H₂O

7. Zmienna w czasie pojemność elektryczna:

WieB:
-"Te wzory SNAFU są niesamowite: ja znalem tylko postać różniczkową: dV = 1/C * i * dt
Albo i = C * dV / dt
No a on to scałkował! Dobre!" (link)

-"Drug sprawa: równanie i = C * V(t) / dt można sparametryzować. Przecież C też może być funkcją czasu i wtedy, zakładając stałe napięcie V(t) = Constant, zmienione równanie pokazuje, że można otrzymać niezerowy prąd, jeśli tylko C się zmienia w czasie.
i = V * C(t) / dt
Można wręcz wytworzyć prąd, bez zewnętrznego źródła energii elektrycznej" (link).

-"Hydrozagadka: ile elektronów?
Ja myślę, że można by na oko, około jednego elektronu na molekułę wody - teoretycznie."

Rysunek 2.

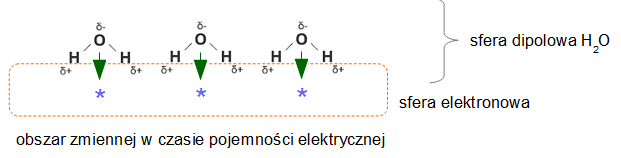
W tej idei dopływ elektronów swobodny czyni statystyczną ingerencję w ruch termodynamiczny cząsteczek wody w sferze dipolowej, a jej wpływ przemieszcza się w czasie głąb wody. Wraz ze wzrostem ilości elektronów swobodnych w sferze elektronowej oraz upływem czasu coraz więcej cząsteczek wody na jej powierzchni ma zorientowany moment dipolowy w stronę sfery elektronowej.

Zatem w tej idei wypada minimum 1 e- swobodny na 4 cząsteczki H₂O, a maksimum 1 e- na 1 H₂O.

8. Względny wzrost pojemności elektrycznej rzędu MILIONA razy:

Pod wskazaną na wstępie notką pt. "Fizyka rzeczy niemożliwych" SNAFU zainspirował opisem względnego wzrostu pojemności elektrycznej w przypadku naelektryzowania powierzchni zewnętrznej kuli oraz zamkniętej powierzchni wewnętrznej.

SNAFU:
"Natomiast, jeśli ładunek uda się pozostawić na wewnętrznej powierzchni -- czyli kula musi wtedy być zrobiona z materiału izolującego -- a dodatkowo zewnętrzną powierzchnię takiej kuli się pokryje warstwą metalu (może być całkiem cieniutka, np. napylona na zewnętrzną powierzchnię -- jakby np. zrobić coś w rodzaju bombki choinkowej, tylko posrebrzonej od zewnątrz, a nie od środka -- to pojemność takiego układu może wzrosnąć w stosunku do pojemności kuli "naelektryzowanej od zewnątrz" -- i to wzrosnąć niebagatelnie, nie tylko kilka, kilkanaście, czy kilkadziesiąt razy -- tylko ten wzrost pojemności może być rzędu MILIONA razy! Ja wcale nie żartuję!"

SNAFU podał również przykład obliczenia pojemności elektrycznej na powierzchni kuli o promieniu R = 1 m:
"Dla obiektu niczym nieotoczonego, trzeba wstawić wartość 1 jako "relative permittivity". Wynik podawany jest Faradach; 1 Farad = 1 Coulomb/1 Volt. Kalkulator podaje, że kola o promieniu R = 1 m ma pojemność 1,112 razy 10 do potęgi -10 Farada. Zatem kula naładowana do napięcia 20 000 V zawiera ładunek:
Q = 20000 Volt * 1,112*10^(-10) Coulomb/Volt = 2,224 *10^(-6) Coulomb, czyli 2,224 mikro-coulomba. Teraz trzeba tylko już podzielić otrzymaną wartość przez ładunek pojedynczego elektronu i w ten sposób dostajemy poszukiwaną liczbę elektronów."

Ułożenie A. Naelektryzowanie powierzchni zewnętrznej.
e = 1,602 × 10^⁻19 C
N_e = 2,224 *10^(-6) Coulomb / 1,602 × 10^⁻19 C
N_e = ~1,39 × 10^13

Ułożenie B. Naelektryzowanie powierzchni wewnętrznej (zamkniętej).
W idei hydroelektronowej - sfera dipolowa H₂O, objętość dipolowa H₂O, sfera elektronowa - zbiornik kulisty:

R = 1 m
V = 4,19 m³
S = 125 663,71 cm²

V_d = S_Z *  D_H2O
V_d = 125 663,71 cm² * 0,27 nm
V_d = 125 663,71 cm² * 0,27 × 10^-7 cm
1 nm = 1 × 10^-7 cm
V_d = 33.929,2 × 10^-7 cm³

N_H2O = V_d / V_H2O

N_H2O = 33.929,2 × 10^-7 cm³ / 0,03 nm³

N_H2O = 33.929,2 × 10^-7 cm3 / 0,03 × 10^-21 cm³

N_H2O = 1.130.973 × 10¹⁴

N_H2O = ~1,13 × 10²⁰ (jeden wprowadzony e- na jeden dipol H₂O → ~1,13 × 10²⁰ elektronów swobodnych)

N_H2O / Ne = 1,13 × 10²⁰ / 1,39 × 10¹³ = 0,81  × 10⁷ = 8,1 × 10⁶

N_H2O (dipol H₂O ~ e-) = ~8 × 10⁶ * N_e

N_H2O (dipol H2O ~ e-) to naelektryzowanie zamkniętej wewnętrznej powierzchni
N_e - naelektryzowanie zewnętrznej powierzchni

Zatem dla potencjału elektrycznego V = const. (potencjał taki sam w obu przypadkach, tj. dla elektryzowania zewnętrznego i wewnętrznego), "potencjału (czyli napięcia w odniesieniu do ziemi) 20 000 Voltów",  jeżeli w powyższej idei nie ma pomyłki w ułożeniu i w obliczeniach, to względem tego, od której strony jest powierzchnia naelektryzowana (powierzchnia zewnętrzna = powierzchnia wewnętrzna zamknięta), pojemność zmienia się - naelektryzowanie wewnętrzne jest rzędu MILIONA razy większe od naelektryzowania zewnętrznego.

Pojemność elektryczna:

Q_a = 20000 Volt * 1,112*10^(-10) Coulomb/Volt = 2,224 *10^(-6) Coulomb

e = 1,602 × 10^⁻19 C

Q_b =  1,13 × 10^20 * 1,602 × 10^⁻19 C = 1,8 *10^1 = 18 C
Przeciętny piorun ujemny niesie prąd elektryczny o natężeniu 30 000 amperów (30 kA) i przenosi ładunek elektryczny o wartości 15 C (kulombów).

Q_a / Q_b = 2,224 × 10^(-6) C / 18 C = 0,13 × 10^(-6)

C = Q/V; C_a = Q_a/V; C_b = Q_b/V

C_a / C_b = Q_a / Q_b

C_b = ( Q_b / Q_a ) * C_a

C_b = (18 C / 2,224 × 10^(-6) C ) * C_a

C_b = ~8 × 10^6 * C_a

9. Miara jonowa puszki w pkt 4 (puszka o objętości 1 dm³):
W idei hydroelektronowej miara jonowa to ilość wprowadzonych elektronów równa 10^-7 mol/dm³ (równoważna stężeniu jonów H⁺ w ramach jonu H₃O⁺ w wodzie w temp. 25 ℃, która wynosi w stanie równowagi 10^-7 mol/dm³):

N_e (e- → H⁺) = 10^-7 * 6,023 ×10²³ = 6,023 ×10¹⁶

N_H2O = 6,4 × 10¹⁷ (jeden wprowadzony e- na jeden dipol H₂O → 6,4 × 10¹⁷ elektronów swobodnych)

Zatem w tym ułożeniu względem 1 dm³ wody ilość wprowadzonych elektronów jest większa od ilości jonów H⁺, a tym samym dla reakcji: H⁺ + e- → H.

10. Bariera przemieszczenia się elektronów do zbiornika (okienko próżnioszczelne, izolator, strefa elektronowa):

SNAFU we wspomnianych komentarzach wytłumaczył zagadnienie elektryzowania obiektów:

SNAFU:
"Otóż, każdy obiekt, jeżeli mu przekazać jakiś ładunek elektryczny (naelektryzować, jak to się czasem mówi, albo "naładować"), wytwarza wokół siebie pole elektryczne. Im więcej ładunku, tym pole silniejsze. Jeśli ładujemy obiekt elektronami, to uzyskuje on ładunek ujemny i pole przez niego wytworzone będzie odpychać elektrony znajdujące się na zewnątrz obiektu. Im więcej tego ładunku będzie w danym obiekcie,  tym silniej będą takie "zewnętrzne" elektrony odpychane -- w szczególności, elektrony nadlatujące z "działka elektronowego". I w pewnym momencie odpychanie stanie się na tyle silne, że nowe elektrony już nie będą mogły do obiektu dotrzeć.

Dalej już nie da się wytłumaczyć bez matematyki -- nie, przepraszam, nie matematyki, to za duże słowo: bez prościutkich rachunków. Otóż, naładowany obiekt uzyskuje elektryczny potencjał -- innymi słowy, napięcie. Jeżeli to napięcie osiągnie wartość 20 000 Voltów, to elektron, żeby do obiektu "wniknąć", musi mieć energię większą, niż 20 000 elektronowoltów (eV). Każdy elektron o energii niższej, niż 20 000 eV, już zostanie odepchnięty, "zawrócony z drogi". Zatem, jeśli używany działka wytwarzającego elektrony o energii kinetycznej 20 000 eV, to możemy obiekt naładować do potencjału (czyli napięcia w odniesieniu do ziemi) 20 000 Voltów."

Elektrony z działa elektronowego przemieszczają się w idei przez okienko próżnioszczelne, izolator i strefę elektronową.

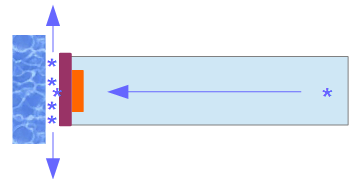
V = 20 000 eV ← Ek (e-) = 20 000 eV

Zatem w czasie przemieszczania się wyemitowanych z działa elektronów "przez trójbarierę" (3B) ich energia kinetyczna ulegnie zmianie: Ek (wyjścia) = Ek (wejścia) - W (3B), czyli energia kinetyczna za 3B równa jest energii kinetycznej przed 3B pomniejszonej o pracę przejścia W(3B), pracę sił hamujących przemieszczenie się przez 3B.

W tej idei, jeżeli elektrony w sferze elektronowej mogą się przesunąć pod wpływem odpychania kolejnego elektronu z działa elektronowego, to ten elektron przemieści się do zbiornika.

W prezentacji wprowadzania elektronów do powietrza za pomocą działa elektronowego poprzez przenikanie ich przez okienko próżniowe - link, YT: "Shooting an electron beam through air" (dostępne tłumaczenie PL)  - "Wystrzeliwanie wiązki elektronów w powietrze. Specjalne okno o grubości 100 nm pozwala elektronom o energii 25 KeV przejść z lampy próżniowej do atmosfery, gdzie uderzają w ekran fluorescencyjny – CRT w powietrzu!" - wspomniane jest o ilości emitowanych elektronów. Autor prezentacji informuje o użyciu maksymalnego natężenia 300 mikroamperów:

1 mikroamper = 1,0 × 10^-6 ampera; 1 A = 1C / 1 s; 1 C to 6,24 × 10¹⁸ ładunków elementarnych
e = 1,602 × 10^⁻19 C
100 μA = 100  × 10^-6 A = 10^-4 A
N_e (100 μA) = 10^-4 * 6,24 × 10¹⁸ =  6,24 × 10¹⁴ elektronów
Zatem w eksperymencie emitowana jest do powietrza w czasie jednej sekundy ilość elektronów rzędu 10¹⁴.

W idei puszki o objętości 1 dm³ względem miary jonowej:
N_H2O = 6,4 × 10¹⁷ (jeden wprowadzony e- na jeden dipol H₂O → 6,4 × 10¹⁷ elektronów swobodnych)
zatem przy emisji o natężeniu N_e (100 μA), emisja w czasie 1000 sekund daje porównywalne wielkości:
N_e (100 μA, czas emisji t = 1000 s) =  10³ * 6,24 × 10¹⁴ elektronów ~ N_H2O = 6,4 × 10¹⁷ elektronów

Wybrane wartości gęstości (temp. 20 °C):
- powietrze ρ_p = 1,205 kg/m³.
- woda ρ_w = 998,2 kg/m³.

Zasięg elektronów w wodzie, czyli odcinek w linii prostej, jaki w niej pokonują torem zygzakowatym w wyniku zderzeń z H₂O, zależy od ich Ek. W eksperymencie emisji elektronów do powietrza autor uzyskuj ok. 8 mm:

*

ps.

Internet:

Fotowtrysk elektronów w wodzie - "Gorące elektrony w wodzie: wtrysk i przyspieszenie ponderomotoryczne za pomocą nanoelektrod plazmonicznych" (link: PL, ANG)

Uzdatnianie wody za pomocą napromieniania wiązką elektronów - "Zarządzanie energią i środowiskiem" (link: PL, ANG)