Poprzednia notka choć wywołała sporą dyskusje, nie była dla mnie pozytywna. Praktycznie tylko jeden bloger zainteresował się jej sensem. Jednak dobre i to. Dzięki temu chce mi się napisać kolejną.
Ta notka wymaga znajomości założeń z poprzednich części z tego cyklu.Nie będę w niej tłumaczył co spada, a co porusza się po orbicie kołowej. Jeśli będą pytania, odpowiem jak zwykle w komentach.
Teraz zajmiemy się badaniem co widzi obserwator w spadającej windzie. Nie będą to pomiary, ale obliczenia. Nic strasznego, żadnej skomplikowanej matematyki. Naszym zadaniem jest obliczenie odległości satelity od obserwatora w spadającej windzie. Przypominam że spadek windy rozpoczyna się gdy satelita mija windę na godzinie 12. Początkowa prędkość spadania windy wynosi zero. Prędkość satelity, to jak zwykle
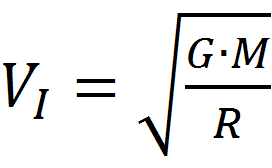
Zmienię jednak jej oznaczenie na Vo (prędkość orbitalna) na samo V. Nasz satelita musi spełniać to równanie, bo inaczej rozważanie nie będą prawdziwe. Schematyczny rysunek przedstawia nasze doświadczenie:
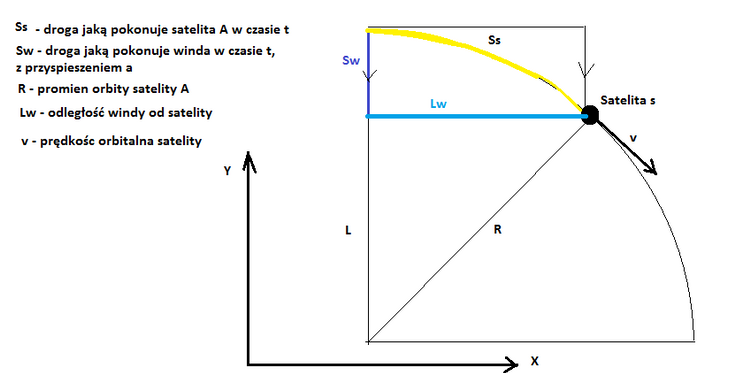
Winda i satelita są w spadku swobodnym, więc pokonują ta sama drogę wzdłuż osi Y. Znając prędkość V satelity wyliczymy drogę jaką on pokonał po czasie t: Ss=vt (kolor żółty)
Drogę spadku windy obliczymy równie łatwo, bo prędkość początkowa równa się zero. Wzór:
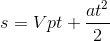gdzie : |a|=g
V początkowa równa się zero, wiec wzór jest skromniejszy:
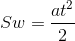wz.1a
Tak więc odcinek L wyliczymy dość prosto jako R-Sw, czyli:
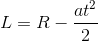wz.1b
Teraz wyliczymy sobie odległość satelity od windy po czasie t:
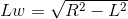, czyli:
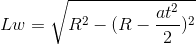wz.1c
Wzór ten oblicza odległość jaka dzieli windę od satelity. To wyliczenie też obrazuje zmianę prędkości satelity w układzie odniesienia (UO) windy. Jednak gdzy to liczyłem nie było dla mnie zaskoczeniem że ta prędkość maleje (odległość rośnie coraz wolniej), ale przebieg tej zmiany. Pokaże wiec wykres funkcji:
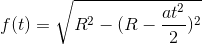
Pierwszy wykres jest dla R=1 i a=1:
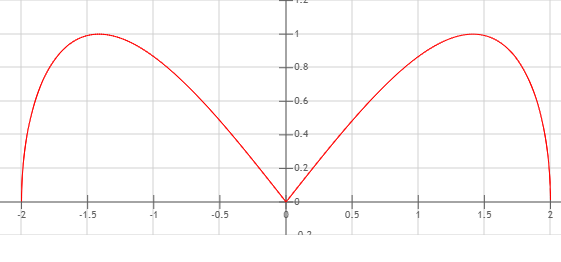
Oczywiście dla naszego przypadku bierzemy wartości dodatnie (na prawo od osi Y).
Dla R=10 oraz a=1:
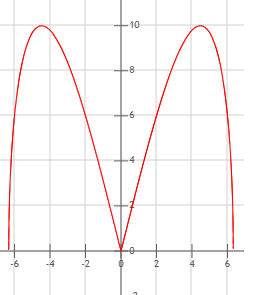
I trzeci wykres dla R=10 i a=10:
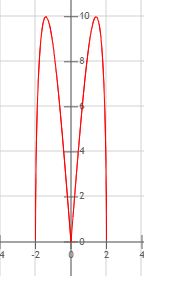
Nie wiem czy to już widać wystarczająco wyraźnie, ale relacja R do a nie jest liniowa. To w sumie nie jest wielkie zaskoczenie, bo a zależy od masy. Jednak jest to jak dla mnie mało intuicyjne. Odbieram to jako pewien czynnik skali. Być może że stosunek a/R ma głębsze znaczenie. Kiedyś się nad tym zastanowię.
Na koniec napiszę jedno. Te wyliczenia są psu na budę. Nie mają żadnego związku z grawitacją, ani spadająca windą. Dla czego jednak o nich napisałem? Odpowiedź jest prosta. Metodologia jest w nich prosta i przygotowuje do właściwych rozwiązań. Ułatwi zrozumienie kolejnej notki.
ps. dla tych co maja czas i ochotę się pobawić, to polecam stronę: rysowanie-wykresow-funkcji
Formuła według zapisu na tej stronie wygląda tak: sqrt(R^2-(R-((ax^2)/2))^2)
x to nasz czas t, a w miejsce R i a podajemy jakieś liczby. Strona rysuje wiele wykresów i jest bardzo intuicyjna. Polecam ją gorąco.
Mam nadzieję ze nie zrobiłem większych błędów i opis jest jasny.
tagi: nauka, fizyka, grawitacja
Inne tematy w dziale Technologie
