Kończąc poprzednia notkę napisałem że tabela ma wadę. Wadę jaka w mojej ocenie wymaga poprawy. Kolumny liczb pierwszych mają ścisłe reguły występowania w nich liczb złożonych. Reguły wyglądają tak:
Lr+x210 dla 7
Lr+x330 dla 11
Lr+x390 dla 13
Lr+x510 dla 17
..... ->oo
Lr to dowolna liczba pierwsza a x to dowolna dowolna porządkowa
Dość łatwo zauważyć że ten wzór można uogólnić do postaci:
Lr+30*x*Lr wz1
Można by się w tym miejscu pobawić w oznaczenie zbioru liczb pierwszych jako wynik różnic w regułach występowania dowolnych liczb w kolumnach 7...29 poza liczbami spełniającymi wz1. Mnie to jednak mało interesuje. Jak ktoś ma taka potrzebę to łatwo sobie to zrobi. To nie całki, różniczki ani żadne macierze.
Natomiast bardzo mnie zainteresowała kolumna 1 oraz liczby pierwsze 2,3 i 5. Kolumny jakie one generują w tabeli 30 elementowej odbiegają od reguł. Dla tego w pierwszej notce z tej serii dałem je do osobnej grupy. Zastanowić się należy czy to ma jakiś sens, czy jest jakiś inny problem. Liczby 2,3,5 nie generują kolumn w jakich pojawiają się liczby pierwsze. Wszystkie liczby w ich kolumnach to liczby złożone. Podstawiając do wzoru wz1 te liczby łatwo się o tym przekonamy. Dowód matematyczny na to twierdzenie nie powinien być specjalnie trudny.
Mamy natomiast kolumnę 1, jaka nie pasuje do schematu. To wada tabeli w moim rozumieniu. Pomimo że tabela wygląda ładnie optycznie, widać że kolumna pierwsza jakoś nie pasuje.
W związku z powyższym uznałem że trzeba tabele przebudować tak by pozbyć się tej anomalii. Na pierwszy strzał poszło wykluczenie z tabeli grupy liczb pierwszych jakie nie pasują do reguł i wyciągnięcie ich jakby przed nawias. Budowanie tabel jest czasochłonne, więc chciałem by zmiany miały jakiś sens. Nie chodziło mi o przypadkowe generowanie tabeli 30.
Wynik generowania nowej tabeli na załączonym obrazku:
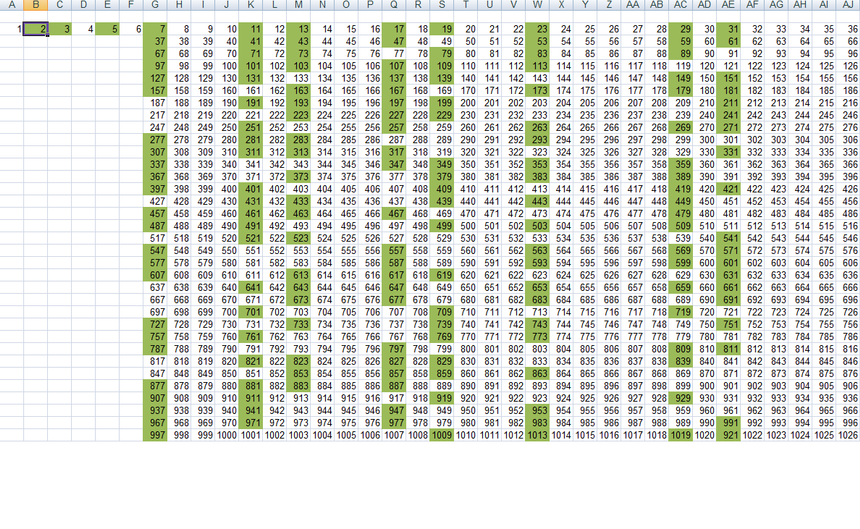
rys1
Kolorem zielonym zaznaczone liczby pierwsze.
Tabela straciła swoją symetryczność optyczną, ale kolumny nie uległy destrukcji. Liczby pierwsze nadal występują w kolumnach 7,11,13,17,19,23,29 i doszła kolumna 31 w miejsce kolumny 1. Symetryczność optyczną tabeli osiągniemy jeśli zbudujemy ją z wierszy po 60 elementów (hyhy czyli liczenie starymi metodologiami na kopy). Są opinie że tabela z 60 pozycjami jest wyższej wagi jak tabela z 30 pozycjami. Nie twierdze że nie. Jednak łatwiej analizować mi tabele 30 liczbowe. Na razie nie odbiłem się od muru, więc pozostanę przy wersji 30 liczbowej.
Popatrzmy teraz czy tak zbudowana tabela rozwiązała mój problem jaki wskazałem na początku tej notki. Zaznaczę więc podzielniki liczby 7:
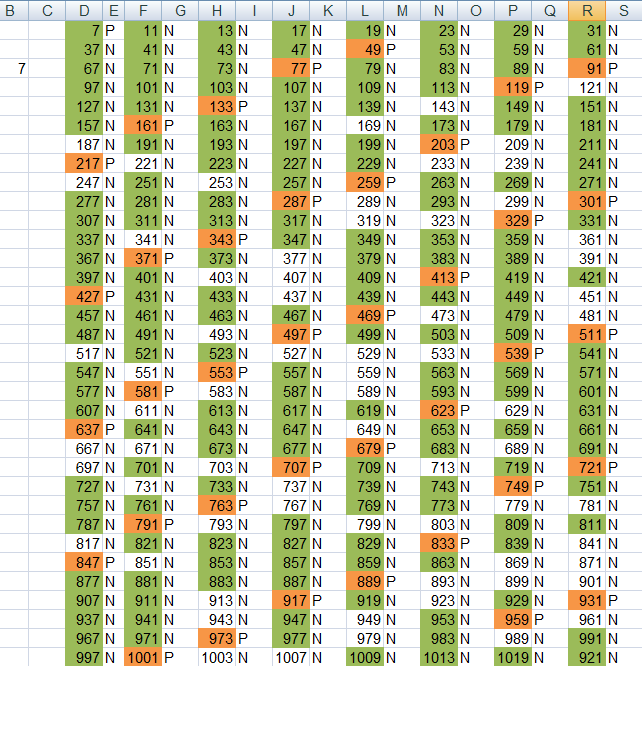
rys2
Tabela w wersji skróconej dla lepszej czytelności. Kolorem czerwonym zaznaczone są podzielniki liczby 7. Pozycje oznaczone jako P i N to miejsca gdzie wpisana jest reguła podzielności w exelu. Tabela nie utraciła reguł jakie były w poprzedniej wersji tabeli. Teraz jednak reguły są ładniejsze. Np liczby złożone podzielne przez 7 są na 1,8,15,22... pozycji. Tak samo podzielne przez 11 są na 1,12,23... pozycji (oczywiście w swoich kolumnach).
Tabela zrobiła się jakby bardziej "cywilizowana". Pokaże jeszcze tabele z liczbami podzielnymi przez 11.
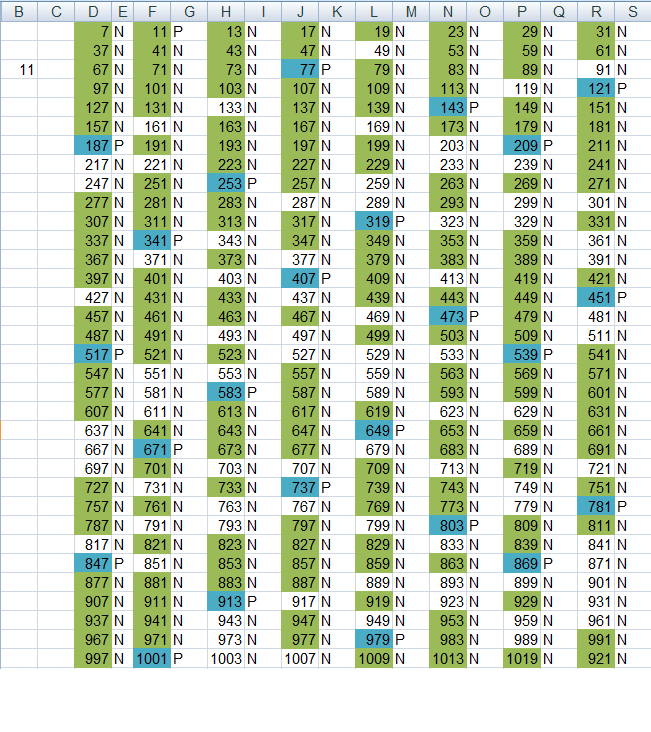
rys3
W wersjach skróconych nie widać węzłów sita Eratostenesa. To jest pewien problem, ale wystarczy pamiętać o tym. To nadal jest Sito Eratostenesa. Wszystko co o nim wiadomo nadal jest w mocy a ja nie buduje żadnych spiskowych teorii. Badam to sito pod kątem liczb złożonych i chce się coś o nich dowiedzieć. Można by dalej lać wodę o rozkładzie liczb złożonych w każdej kolumnie. Jednak to nie ma większego sensu, bo ten rozkład jest ustalony przez wz1 z tej notki. Miało by to rację tylko na gruncie estetycznym (tak mi się wydaje). W kolejnej notce zaproponuje inne obrazowanie sytuacji. Będzie mniej czytelne niż tabela, ale widzę w nim pewien potencjał.
Pozdrawiam
tagi: nauka, matematyka, fizyka, Eratostenes, liczby pierwsze
Inne tematy w dziale Technologie

