Obraz jaki widzimy (lub jaki przyjmujemy do wiadomości) jest kompilacją wielu, a czasem nieskończenie wielu obrazów istniejących czasem jednocześnie. Na pierwszy rzut oka wydaje się to irracjonalne. Ja jednak uważam że nie. Napiszę więc dla czego tak uważam na podstawie prostego przykładu.
Popatrzmy na liczbę np 5. To jedna, jedyna cyferka. Czy aby na pewno? Zastanówmy się co znaczy ten znak 5. Nie trzeba filozofa by wiedzieć że 2+3=5. No tak, ale 4+1 też równe jest 5. -3+8 też jest równe 5. Bez specjalnego zmęczenia możemy z całą pewnością powiedzieć że dla każdego n ze zbioru liczb rzeczywistych istnieje inna liczba m dla jakiej równanie n+m=5 jest prawdziwe. Rozumowanie możemy rozszerzyć dla innych zbiorów liczb i będzie prawdziwe. Pytanie więc brzmi co tak naprawdę jest pod znakiem 5? Ile tak naprawdę elementów jest ukrytych pod znakiem 5? Teoria mnogości mówi że zbiór nieskończony do jakiego dodam inny zbiór nieskończony, da nam też zbiór nieskończony. Dla czego więc zawsze istnieje takie m jakie dodane do n równe jest 5, a nie nieskończenie wiele rozwiązań? Musi istnieć jakaś reguła jaka precyzuje, że z dwóch zbiorów nieskończonych można dobrać tak elementy by n+m równe było 5. Takie pytania zadawałem sobie jeszcze w szkole. Nadal nie znam na nie odpowiedzi, ale bardzo chcę gonić tego króliczka.
Ten filozoficzny wstęp jest zwiastunem kolejnych notek. Być może natrafiłem na pewien ślad. Jednak nim do tego dojdę, muszę domknąć poprzednie notki. Być może to będzie trochę zaskakujące, ale było w moim mniemaniu nieodzowne. Poprzednio wskazałem regułę, jaka jest cykliczna w tabeli liczb utworzonej z pocięcia osi liczbowej na 30 elementów. Słusznie bloger @Robbaks zauważył że ta reguła obowiązuje nie tylko dla kolumn z liczbami pierwszymi, ale dla każdej z kolumny tej tabeli. Jednak kolumny w jakich nie ma liczb pierwszych, nie dają nam żadnej podpowiedzi o co może chodzić. Dla tego nadal będę rozpatrywał tylko kolumny w jakich pojawiają się liczby pierwsze.
Pytanie na dzisiaj to takie: czemu liczba 7 jest tak unikatowa. Odpowiedz na to pytanie jest wręcz banalna. Liczba 7 nie jest żadnym unikatem. W tej tabeli jest jedną z nieskończonej ilości liczb jakie maja swoje reguły występowania. Pokażę więc tabele dla kilku innych liczb. Najpierw wiec podzielniki pierwszej liczby (hyhy)pierwszej, czyli 2:
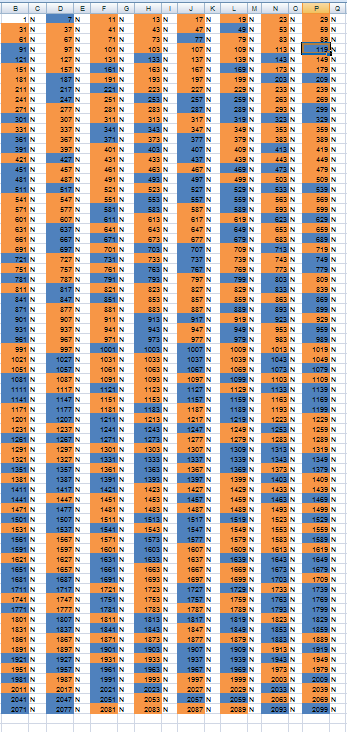
rys1
oznaczenia:
kolor czerwony liczby pierwsze
kolor niebieski liczby złożone
kolor biały to wynik z funkcji sprawdzającej podzielność. N oznacza że jest niepodzielna (w tym wypadku liczba nie jest podzielna przez 2), P podzielna (w tym wypadku podzielna przez 2)
Żadna liczba z kolumn zawierających liczby pierwsze nie jest podzielna przez 2. Ta sama procedura dla liczby 3 daje ten sam wynik. Kolejna liczba jest parzysta (4), więc nie ma co bardzo się spodziewać że wynik testu będzie pozytywny (bo w kolumnach 7,11,13,17,19,23 i 29 są tylko liczby nieparzyste. Liczba 5 choć jest nieparzysta nadal nie ma dzielników. Tak samo 6, a 7 omawiałem poprzednio. Kolumny zawierają liczby podzielne przez 7. 8 jest parzyste wiec odpada z automatu. A 9? Niestety też nie. Czemu więc pisałem że takich liczb jak 7 jest nieskończenie wiele? To nie takie skomplikowane jakby się zdawało. Kolumny zawierające liczby pierwsze, posiadają liczby złożone ale tylko takie, jakie są podzielne przez liczby pierwsze. Nie może to być liczba złożona, ani liczba nieparzysta. To musi być liczba pierwsza. Kolejna tabelka pokazuje liczby podzielne przez 11:
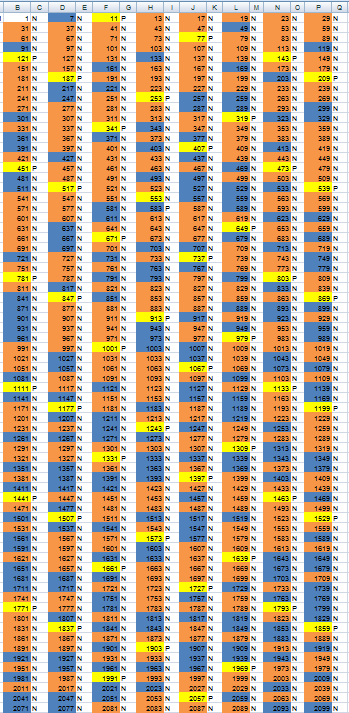
rys2.
Kolorem żółtym zaznaczone liczby podzielne przez 11. Jak widać liczba podzielna przez 11 występuje co 11 wiersz w każdej kolumnie. Bezwzględna odległość na osi liczbowej tych podzielników jest o 330, czyli każdy kolejny podzielnik występuje co 330 pozycji. Podobnie jak w przypadku podzielników liczby 7, możemy wskazać regułę:
Lr+x330 ### wz2
Lr to pierwsza liczba w każdej kolumnie jak jest podzielna przez 11 (czyli kolumn 7,11,17,19,23,29)
x to liczba porządkowa (jak w poprzedniej notce)
Kolejne badanie dla liczby 13:
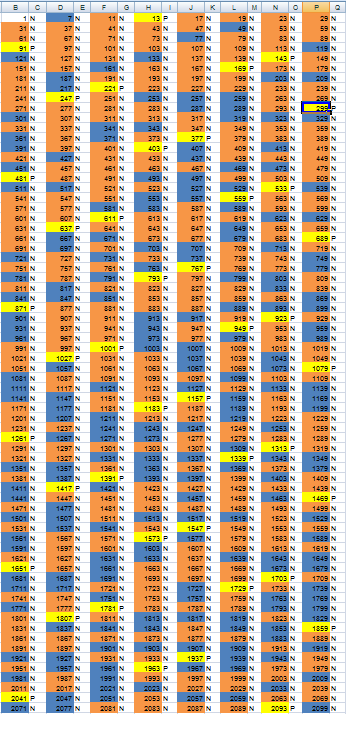
rys3
Ponownie mamy taka samą regułę. Jedyna zmiana to to, że powtórka w wierszach jest co 13, a liczba Lr=390. Jeśli ktoś potrzebuje prześle plik xml w jaki można sobie sprawdzić dowolny podzielnik. Wzór można zmałpować z poprzednich tabeli. Co zasługuje na uwagę, to liczba Lr, jaka ma wartości 210, 330 i 390. Wzrost tej liczby nie jest liniowy. Niestety to nie jedyny problem. Tabela ma poważna wadę. Pierwsza kolumna zaczyna się od liczby 1, a pozostałe od wartości swoich podzielników. Świadczy to o tym ze tabela jeszcze nie jest optymalna i wymaga poprawek.
Kiedy pierwszy raz liczyłem te tabele, wydawało mi się że już macam się z kurką. Okazało się jednak że to króliczek i dał drapaka w krzaki. Musiałem ponownie przewartościować swoje widzenie, bu wygrzebać go (króliczka) z tych zarośli. Kolejna notka będzie o tym jak te krzaki rozsadzić, bo zobaczyć więcej.
edit: w kolumnach 7,11,13,17,19,23 i 29 występują liczby złożone jakie mają podzielniki tylko w zbiorze liczb pierwszych. Nie ma ograniczenia że do liczby 29. Jeśli rozwiniemy tabelę na więcej wierszy, pojawią się podzielniki przez kolejne liczby pierwsze. Nie zrobiłem tego tylko dla tego że obrazki i tak są już mało czytelne. Przy większej tablicy, ich czytelność wykluczyła by jakiekolwiek zrozumienie reguł jakie występują w tabeli.
ps. dołożyłem wszelkich starań by tabele były bez błędów a tekst możliwie zrozumiały.
cdn
tagi: nauka, matematyka, fizyka, Eratostenes, liczby pierwsze
Inne tematy w dziale Technologie

