Szczegóły modelu heliocentrycznego Kopernika

Jest to kolejna notka przedstawiająca przyczyny i historię powstania modelu Kopernika. Osoby, które trafiły tu po raz pierwszy (albo zapomniały, o czym pisałem), proszone są o zapoznanie się z wcześniejszymi tekstami. Należy zacząć od Dlaczego Kopernik stworzył system heliocentryczny?, po czym posuwać się zgodnie z linkami zamieszczonymi na końcu każdej kolejnej notki.

Jest rzeczą zdumiewającą, że we współczesnych opiniach na temat modelu Kopernika tak często pojawiają się nieścisłości, a nawet przekłamania. Dla przykładu, gdzieś wyczytałem, że Kopernik traktował swój model tylko jako schemat rachunkowy służący do obliczania położeń planet na niebie, a nie jako prawdziwą wizję Wszechświata. Jest to kompletna bzdura! Świadczy o tym choćby cytat zamieszczony w poprzedniej notce. Takie fałszywe stwierdzenia wynikają zapewne z faktu, że mało kto zechciał zapoznać się z oryginalnymi pracami Kopernika lub choćby ze szczegółowymi analizami. Mamy do czynienia z zabawą w głuchy telefon: ktoś coś powiedział albo napisał, inny powtórzył jakiś fragment wyrwany z kontekstu, kolejny dodał własną interpretację... Spróbujmy więc wyprostować niektóre kwestie i przyjrzyjmy się szczegółom systemu Kopernika.

Formalnie rzecz biorąc, nazwa „model heliocentryczny” jest niepoprawna, gdyż Słońce nie znajduje się w centrach orbit planetarnych, ale jest względem nich przesunięte. Być może bardziej adekwatne byłoby określenie „model heliostatyczny” podkreślające nieruchomość Słońca, jednak ponieważ pojęcie „heliocentryzm” od wieków przyjęło się w literaturze, głupotą byłoby zmieniać je na siłę.

Od czasu do czasu można się spotkać z deprecjonującą opinią, że właściwie jedyną rzeczą, jaką uczynił Kopernik, było przeniesienie układu odniesienia z Ziemi na Słońce. W sumie – nic szczególnie istotnego... Gdyby to nawet była prawda, trzeba pamiętać, że przechodzenie od jednego układu odniesienia do innego jest procedurą powszechnie stosowaną dzisiaj – naukowcy skaczą z jednego układu na drugi i wybierają sobie taki, jaki im najbardziej pasuje do prowadzenia konkretnych obliczeń – ale w epoce Kopernika nikt czegoś takiego nie robił. Już sam fakt zmiany układu odniesienia byłby w jego czasach czymś absolutnie nowatorskim.

Jednakże model Kopernika jest czym znacznie więcej niż tylko prostym przeniesieniem punktu odniesienia z Ziemi na Słońce. To prawda, że z punktu widzenia współczesnej nauki można zastąpić opis heliocentryczny ekwiwalentnym opisem geocentrycznym, ale nie znaczy to, że każdy model heliocentryczny jest równoważny każdemu modelowi geocentrycznemu! Model Kopernika nie jest prostą transformacją modelu Ptolemeusza. Przypomnijmy sobie schematyczny rysunek wewnętrznych części modelu Ptolemeusza (Słońce porusza się tuż za strefą Wenus):

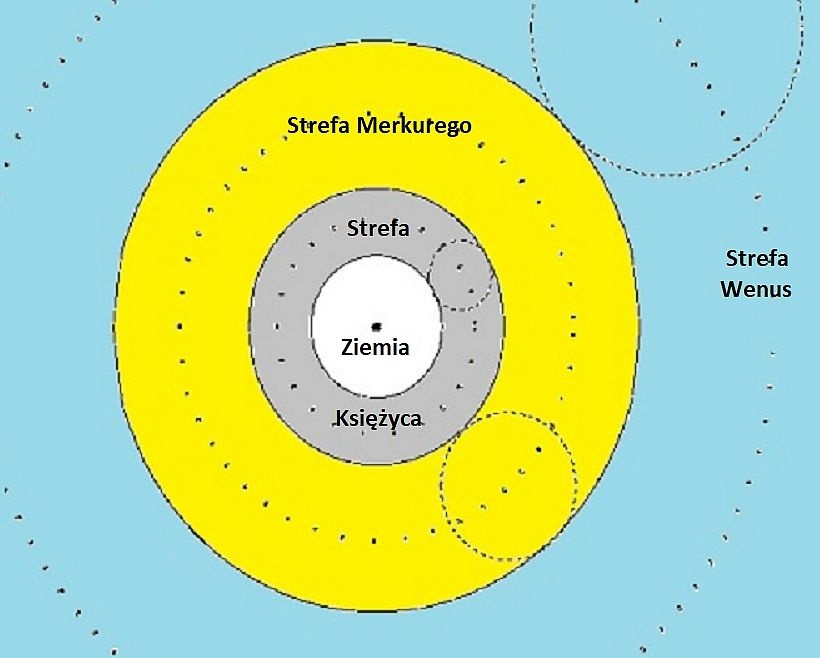
Gdyby Kopernik po prostu przetransformował model Ptolemeusza z Ziemi na Słońce, kolejność planet byłaby niepoprawna: Wenus obiegałaby Słońce bliżej niż Merkury!

Jest jeszcze jedna różnica między Ptolemeuszem a Kopernikiem. W modelu Ptolemeusza niektóre z epicykli są bardzo duże – zwłaszcza te, które mają tłumaczyć pętle na niebie. Kopernik je usunął, a za to wprowadził malutkie epicykle zastępujące ptolemeuszowy ekwant. W literaturze anglojęzycznej spotkałem się z określeniem „epicyclets”, które trudno przetłumaczyć na język polski – „epicykliki” brzmią durno, a „epicyklunie” jeszcze głupiej.

Inny zarzut, jaki Kopernikowi stawiają niektórzy, jest taki, że jakoby zaprezentowane przez niego kształty orbit nie są poprawne, a właściwe rozwiązanie znalazł dopiero Kepler, który dopasował do orbit elipsy. Ten zarzut też jest zdecydowanie chybiony. Kopernik, tak jak jego poprzednicy, opisywał ruch planet za pomocą deferentów i epicykli, ale przecież kombinacja deferentu i epicyklu daje bardzo dobre przybliżenie ruchu po elipsie. Ilustruje to poniższy rysunek:

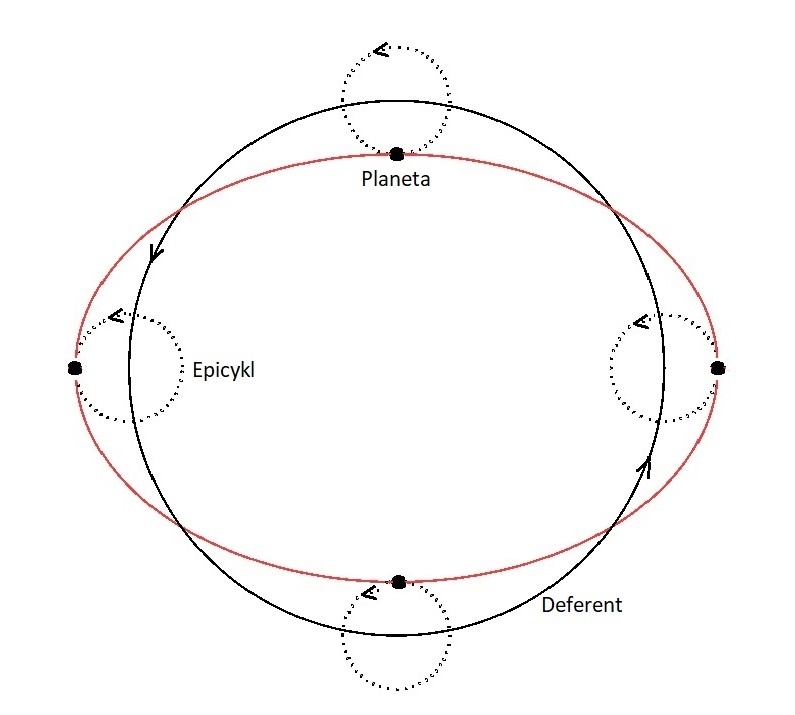
Jeszcze lepszą zgodność uzyskamy, gdy zwiększymy liczbę epicykli. Zastosowanie epicykli do opisu orbit eliptycznych przypomina przybliżanie funkcji okresowych za pomocą kombinacji funkcji trygonometrycznych. Wszyscy, którzy mieli na studiach wykład z analizy matematycznej, wiedzą że każdą funkcję okresową można aproksymować z dowolną dokładnością sumą odpowiednio dobranych sinusów i cosinusów – jest to tak zwane rozwijanie w szereg Fouriera. Im więcej sinusów i cosinusów, tym dokładniejsze przybliżenie. W opisie orbit epicykle są odpowiednikami tychże sinusów i cosinusów. I faktycznie, można pokazać, że opis za pomocą mimośrodowego deferentu i jednego epicyklu jest tożsamy, z dokładnością do wyrazów pierwszego rzędu w mimośrodzie, z niejednostajnym ruchem po elipsie. Ponieważ mimośrody orbit wszystkich planet nie są duże, to ich kształty, przedstawione przez Kopernika w O obrotach, dobrze odpowiadają rzeczywistości. Biorąc pod uwagę jakość obserwacji, jakimi dysponował, trudno im cokolwiek zarzucić. Tak naprawdę Kepler, mając znacznie lepsze dane, uprościł tylko opis Kopernika i uczynił go dokładniejszym.

Pisząc to, nie zamierzam w żaden sposób umniejszać ogromnych zasług Keplera. Prawa kinematyki planet, odkryte przez Keplera, stanowiły kamień milowy na drodze do zrozumienia grawitacji.

I teraz dochodzimy do gigantycznej wręcz przewagi, jaką miał model Kopernika nad modelem Ptolemeusza. Kolejność planet, jaką podał Aleksandryjczyk, nie była przez niego wyznaczona, ale odgadnięta. Ptolemeusz próbował też ustalić odległości do planet, ale poniósł kompletną porażkę. Zmuszony był wprowadzić dodatkowe założenie – konkretnie takie, że apogeum każdej planety odpowiada perigeum kolejnej. Jest ono absolutnie niezgodne z prawdą. Natomiast Kopernik, opierając się na swojej koncepcji, mógł w naturalny sposób wyznaczyć nie tylko kolejność planet, ale i względne rozmiary ich orbit planetarnych. Mówiąc dzisiejszym językiem, podał je w jednostkach astronomicznych. (Jednostka astronomiczna to średnia odległość Ziemi od Słońca).

Aby zrozumieć, w jaki sposób Kopernik otrzymał swoje wyniki, przyjmijmy upraszczające założenie, że Ziemia i inne planety poruszają się ruchem jednostajnym po okręgach leżących w jednej płaszczyźnie. Dla większości planet (z wyjątkiem Merkurego) nie jest to założenie złe. Szczególnie prostą sytuację mamy w przypadku planet wewnętrznych, czyli takich, których orbity leżą wewnątrz orbity Ziemi. Są to Merkury i Wenus. Wystarczy dla nich mierzyć tak zwaną elongację, czyli kąt ε, jaki tworzą ze Słońcem na sferze niebieskiej. Gdy elongacja jest największa, Słońce S, planeta P i Ziemia T ustawione są w trójkąt prostokątny:

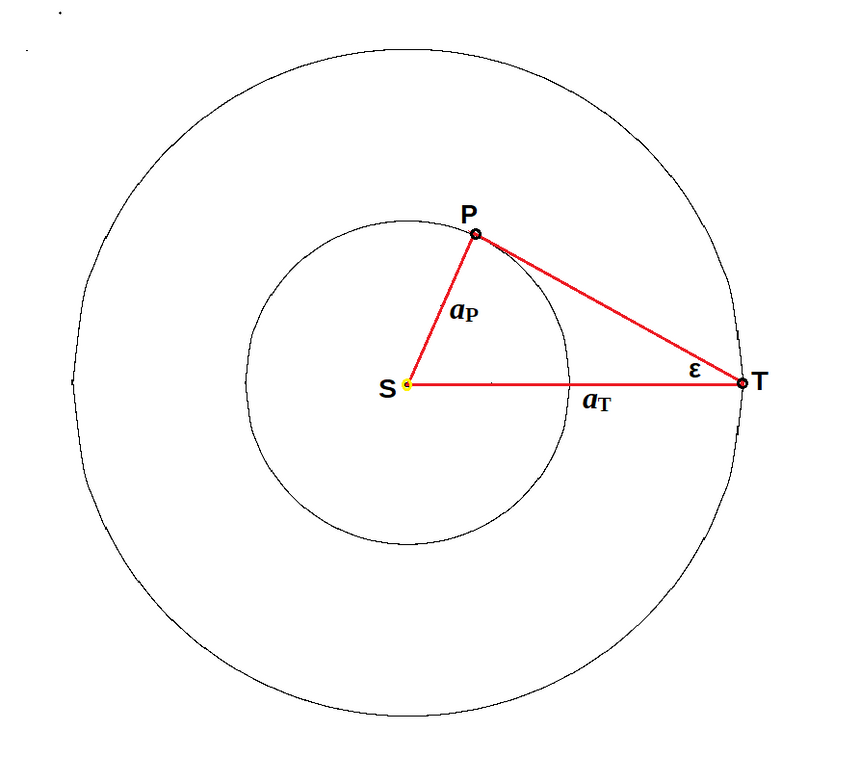
Wówczas, oczywiście, sin ε = a_P/a_T, gdzie a_P i a_T oznaczają odpowiednio promień orbity planety i promień orbity Ziemi. A zatem, znając maksymalną wartość elongacji, natychmiast otrzymujemy względny promień orbity planety.

Trochę bardziej skomplikowane jest wyznaczanie promieni orbit planet zewnętrznych: Marsa, Jowisza i Saturna. Dla tamtejszego obserwatora elongacja Ziemi jest największa, gdy dla nas kąt między planetą a Słońcem wynosi 90º. Taką sytuację nazywamy kwadraturą. Ale jak znaleźć ε? Ponieważ nie znajdujemy się na planecie zewnętrznej, nie można go zmierzyć, lecz trzeba wyznaczyć w sposób pośredni. Należy mianowicie zmierzyć czas między jakimś innym charakterystycznym układem na niebie a kwadraturą. Takim charakterystycznym układem może być opozycja planety, czyli sytuacja, w której planeta znajduje się dokładnie po przeciwnej stronie niż Słońce:

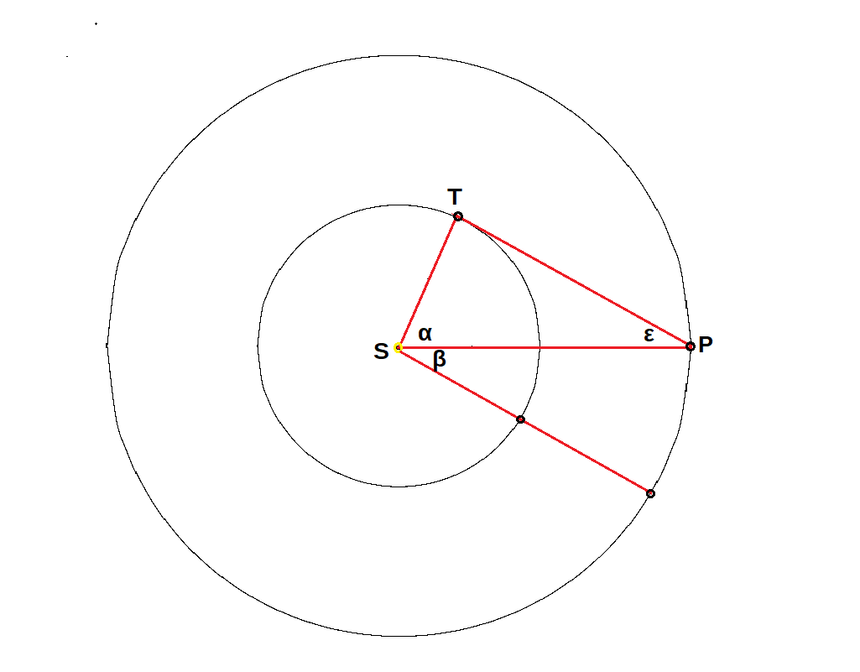
Między opozycją a kwadraturą upływa czas t_ok. W tym czasie Ziemia T przemieszcza się na orbicie o kąt α+β. Ponieważ Ziemia dokonuje obiegu w ciągu jednego roku, a my przyjęliśmy, że porusza się ruchem jednostajnym, kąt ten można wyliczyć z proporcji:

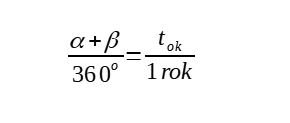
W tym samym czasie planeta zewnętrzna przemieszcza się o kąt β, który można obliczyć w analogiczny sposób:

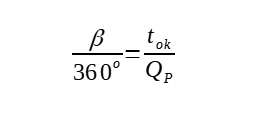
gdzie Q_P jest okresem obiegu planety wokół Słońca. Znając kąt β, wyznaczamy kąt α i możemy obliczyć kąt ε.

Mniej więcej w ten sposób postępował Kopernik i otrzymał następujące względne odległości planet od Słońca:

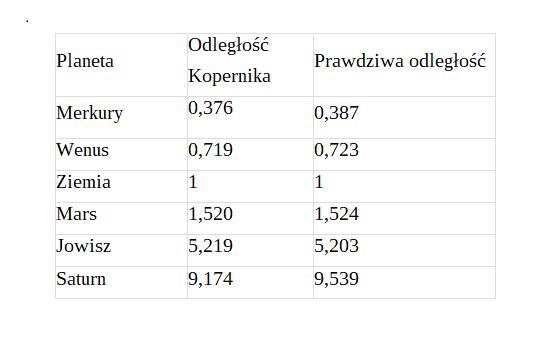
Jak widać, wyniki jakie otrzymał Kopernik, są naprawdę dobre. Jego obraz układu planetarnego jest bardzo zbliżony do prawdziwego.

Niestety, za czasów Kopernika bezwzględne odległości do Słońca i planet nie były wyznaczone poprawnie. Za odległość Ziemi do Słońca przyjmowano wartość otrzymaną w Starożytności przez Arystarcha, która była 19 razy mniejsza od rzeczywistej. Oceny zgodne z prawdą co do rzędu wielkości uzyskano dopiero w 2. połowie XVII wieku, a bliską rzeczywistości wartość jednostki astronomicznej otrzymano w 1761 roku (patrz moja notka Halley: magnetyzm, komety i Wszechświat).

Ciąg dalszy nastąpi.