Jest to czwarta notka z serii; przed przeczytaniem prosiłbym o zapoznanie się z poprzednimi:
Dlaczego Kopernik stworzył system heliocentryczny?
Reakcje na wyzwanie Platona
Ku astronomii predyktywnej
Przez kolejne trzy wieki w astronomii koncepcyjnie niewiele się działo. Wreszcie w egipskiej Aleksandrii pojawił się uczony, który zbudował model matematyczny zawierający w sobie całość ówczesnej wiedzy o Kosmosie. Był to Klaudiusz Ptolemeusz (ok. 100-ok. 170 n.e.), zwany w skrócie Ptolemeuszem. O jego życiu wiemy niewiele, poza tym, że miał bardzo szerokie zainteresowania. Napisał dzieło Geografia, które stanowiło podsumowanie ówczesnej wiedzy o Ziemi i aż do czasów Odrodzenia służyło jako podstawowe kompendium. Zajmował się astrologią, optyką i teorią muzyki, najbardziej znany jest jednak jako autor Almagestu – pracy, która przez następne półtora tysiąca lat stanowiła Biblię astronomów. Przedstawiała ona całościowy obraz Wszechświata oraz metody obliczania tak zwanych efemeryd, czyli przewidywanych pozycji planet na nieboskłonie. (Oryginalny tytuł pracy to Synteza matematyczna, zaś słowo „Almagest” jest skrótem zniekształconego tytułu jego arabskiego tłumaczenia i pod taką nazwą dzieło to stało się ogólnie znane). Jedną z motywacji do opracowania Almagestu musiała być astrologia. Znajomość położenia planet na niebie w różnych momentach bez konieczności prowadzenia ciągłych obserwacji bardzo ułatwia przecież stawianie horoskopów.
Model Ptolemeusza był rozszerzeniem modelu Hipparcha. Ponieważ obu astronomów dzieliło 300 lat, zebrane w tym czasie kolejne obserwacje umożliwiły przeprowadzenie weryfikacji przewidywań Hipparcha. Okazało się, że mimośrodowy opis ruchu Słońca zgadzał się z pomiarami i Ptolemeusz mógł go włączyć do swego modelu zasadniczo bez zmian. Sprawdził jednak także model z deferentem i epicyklem i doszedł do wniosku, że nie można stwierdzić, który z obu modeli jest lepszy, gdyż oba równie dobrze pasują do obserwacji.
Na poniższym video można obejrzeć niezłą animację pokazującą oba modele ruchu Słońca:
Gorzej było z ruchem Księżyca. Położenie tego ciała niebieskiego w okolicach nowiu i pełni pasowało do modelu Hipparcha, ale w pozostałych momentach już nie. Nie ma w tym nic dziwnego: Hipparch stworzył opis ruchu Srebrnego Globu na podstawie historycznych zapisów o zaćmieniach, które występują zawsze wtedy, gdy Księżyc jest albo w nowiu (zaćmienie Słońca), albo w pełni (zaćmienie Księżyca). Hipparch nie miał wystarczająco dużo danych, żeby poprawnie odtworzyć ruch Księżyca poza nowiem i pełnią. Ptolemeusz już takie dane miał, co zmusiło go do dokonania poprawek i wprowadzenia dodatkowych ruchów.
Model Ptolemeusza znakomicie odtwarzał pozycje Księżyca na niebie w ciągu całego cyklu, ale stwarzał poważny problem, na który zwrócili uwagę późniejsi astronomowie. Z zastosowanej przez uczonego kombinacji deferentu i epicykli wynikało, że Srebrny Glob w punkcie orbity najdalszym od Ziemi (tak zwanym apogeum) znajduje się w odległości 64 promieni ziemskich, natomiast w punkcie najbliższym (perigeum) – w odległości tylko 33 promieni Ziemi. Tak wielka, prawie dwukrotna różnica odległości powinna implikować łatwo zauważalne zmiany w obserwowanym rozmiarze Księżyca. No a takich zmian przecież nie dostrzegamy...
Ptolemeusz nie ograniczył się do opisu ruchów Słońca i Księżyca, ale opracował także modele dla pozostałych pięciu planet. Ciekawy jest sposób, w jaki ustalił ich kolejność. Oczywiście, najbliżej Ziemi znajduje się Księżyc, gdyż porusza się najszybciej po niebie. Najdalej mieści się sfera gwiazd stałych. Najbliżej niej powinien być Saturn, ponieważ on najwolniej przemieszcza się na ich tle. Jowisz porusza się trochę szybciej, a Mars jeszcze szybciej, dlatego muszą one znajdować się odpowiednio bliżej Ziemi.
Najtrudniej było ustalić kolejność Słońca, Merkurego i Wenus. Patrząc z Ziemi, i Merkury, i Wenus nie oddalają się zbytnio od Słońca. Merkury jest zawsze tak blisko Słońca, że okazje do jego obserwacji są bardzo rzadkie, a może zostać zauważony wyłącznie tuż przed i tuż po wschodzie bądź zachodzie Słońca. Ptolemeusz uznał, że planety, dla których zmiany odległości od Słońca na sferze niebieskiej są ograniczone, powinny być od niego bliżej; uczciwie przyznał jednak, iż jest to czyste zgadywanie. Porządek Wszechświata według Ptolemeusza wyglądał zatem następująco: nieruchomą Ziemię obiegają w kolejności Księżyc, Merkury, Wenus, Słońce, Mars, Jowisz i Saturn, a wokół nich kręci się sfera gwiazd stałych.
Usiłując jak najlepiej odtworzyć ruchy planet na niebie Ptolemeusz stwierdził, że do tego celu nie wystarczą deferenty, mimośrody i znaczna nawet liczba epicykli, zmuszony był więc wprowadzić dodatkową konstrukcję geometryczną. W jego modelu środek epicyklu nie porusza się po deferencie ruchem jednostajnym, ale zmiennym. Prędkość tego ruchu jest taka, że dla obserwatora znajdującego się w pewnym punkcie zwanym ekwantem wydaje się być stała. Czyli, gdybyśmy siedzieli w ekwancie, widzielibyśmy że środek epicyklu porusza się jednostajnie po niebie. Ptolemeusz umieścił ekwant na prostej przechodzącej przez Ziemię i środek deferentu po drugiej stronie niż Ziemia, w takiej samej odległości od środka:
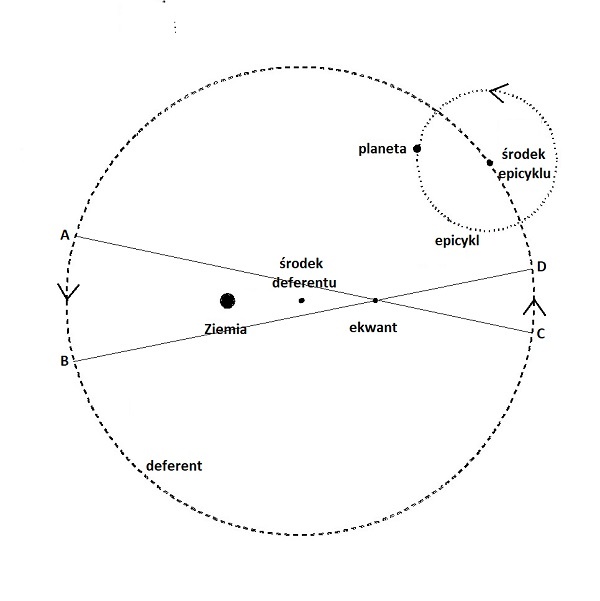
Model ruchu planety z ekwantem. Środek epicyklu przemieszcza się z punktu A do punktu B w takim samym czasie co z punktu C do punktu D.
Wprowadzenie ekwantu łamało zasady przyjęte w filozofii Arystotelesa, gdyż w miejsce ruchu jednostajnego po okręgach wprowadzało ruch niejednostajny. Ptolemeusz postąpił tak, jak powinien postępować każdy uczony: jeżeli wyniki doświadczalne nie pasują do modelu opartego na pewnych założeniach, należy podjąć próbę zmiany założeń, a nie na siłę naciągać wyniki. Arystotelesowski obraz świata zapuścił jednak korzenie w umysłach filozofów tak mocno, że ekwant stał się przedmiotem ostrej krytyki ze strony uczonych starożytnych i średniowiecznych, zarówno chrześcijańskich, jak i islamskich. Jak widzieliśmy, Ptolemeusz sam wprowadzał dodatkowe założenia, gdy uznał to za uzasadnione – choćby wtedy, gdy ustalał kolejność ciał niebieskich; założenia te nie stały wszelako w sprzeczności z ówczesnymi obserwacjami.
W modelu Ptolemeusza występuje jeszcze jedna charakterystyczna osobliwość. Dla wszystkich planet z wyjątkiem Księżyca okres jednego z wykonywanych przez nie ruchów wynosi dokładnie jeden rok. Oczywiście Słońce okrąża Ziemię w ciągu jednego roku, ale ten jeden rok pojawia się też w ruchach innych ciał niebieskich. W przypadku Merkurego i Wenus, czyli planet, które zdaniem Ptolemeusza leżą bliżej Ziemi niż Słońce, jeden rok to okres obiegu epicyklu po deferencie; z kolei dla planet dalszych od Słońca – Marsa, Jowisza i Saturna – jeden rok to okres obiegu planety po epicyklu. Dziś wiemy, że ten rok, obecny w opisie ruchu planet, to odbicie faktycznego ruchu Ziemi wokół Słońca, ale w modelu Ptolemeusza nie było dla niego żadnego głębszego uzasadnienia. Zastanawiający jest fakt, że aż do czasów Kopernika nikt na ten szczegół nie zwrócił większej uwagi.
Oprócz Almagestu Ptolemeusz napisał jeszcze jedno dzieło astronomiczne: Hipotezy planetarne. Kierując się przesłankami bardziej filozoficznymi niż obserwacyjnymi przyjął w nim kolejne założenie, a mianowicie, że między strefami, w których poruszają się poszczególne planety, nie ma pustej przestrzeni. Innymi słowy, maksymalna odległość jednej planety od Ziemi – odległość jej apogeum – jest jednocześnie minimalną odległością (odległością perigeum) kolejnej planety. I tak, odległość apogeum Księżyca odpowiada odległości perigeum Merkurego; odległość apogeum Merkurego to także odległość perigeum Wenus; itd. Pokazuje to poniższa ilustracja:
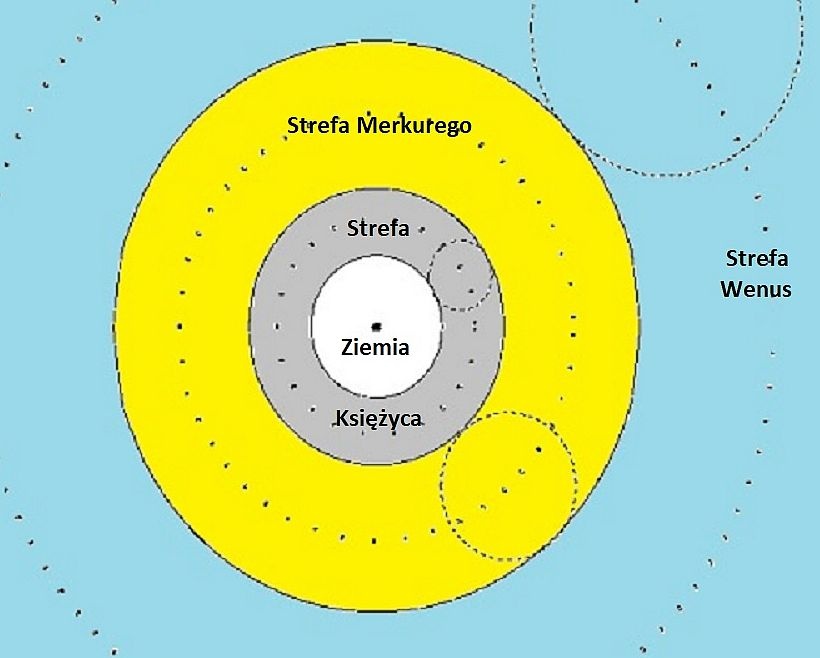
Schemat wewnętrznych części modelu Ptolemeusza
Jeżeli zatem odległość apogeum Księżyca wynosi (jak to wynikało z modelu) 64 promienie Ziemi, tyle samo musi wynosić odległość perigeum Merkurego. Z systemu epicykli koniecznych dla odtworzenia ruchów Merkurego można wyznaczyć apogeum jego orbity, które jest jednocześnie perigeum Wenus. Czyniąc kolejne kroki dochodzimy w ten sposób do apogeum Saturna, będącego również promieniem sfery gwiazd stałych. Zgodnie z obliczeniami Ptolemeusza wynosi on niecałe 20 tysięcy promieni Ziemi, czyli jakieś 120 milionów kilometrów. Dla nas ta wartość wydaje się koszmarnie mała (prawdziwa odległość Słońca to 150 milionów kilometrów, jest zatem większa niż wyznaczona przez Ptolemeusza odległość do gwiazd), ale Starożytni uważali ją za kolosalną.
Ptolemeusza można podziwiać za znakomitą wyobraźnię przestrzenną. Był on w stanie zwizualizować sobie ruchy wszystkich planet w taki sposób, aby można je było rozłożyć na składowe kołowe. Wyznaczone przez niego liczbowe parametry tych składowych umożliwiały zarówno jemu, jak i jego następcom obliczanie efemeryd (czyli przewidywanych położeń) wszystkich planet z ogromną jak na owe czasy dokładnością. Z drugiej strony, jego model przypomina obiad ugotowany przez kiepskiego kucharza. Dobry kucharz zna smak wszystkich ingrediencji i ich kombinacji, dlatego przyrządzając jakąś potrawę ma od razu przygotowane potrzebne składniki w odpowiednich ilościach. Gotując zupę może wrzucić wszystko do garnka, zalać wodą i spokojnie czekać przez przewidziany wcześniej czas. Dla odmiany zły kucharz musi w kółko próbować. Zupa jest za mało kwaśna? Doleję trochę octu. O, teraz jest zbyt kwaśna; dosypię nieco cukru. Ale teraz jest raczej mdła; trzeba dodać przyprawy. I tak dalej... Na zakończenie otrzymujemy potrawę, która może być nawet całkiem smaczna, ale tak naprawdę nie wiadomo dlaczego. I taki był właśnie model Ptolemeusza, w którym siedem ciał niebieskich wykonywało w sumie ponad 70 różnych ruchów po deferentach i epicyklach: działał dobrze, ale jego składniki sprawiały wrażenie wielkiej przypadkowości. Nie było w nim żadnej głębszej logiki.
Widzimy zatem, że model Ptolemeusza opierał się na pracach wcześniejszych uczonych. Był on ostatnim ogniwem łańcucha kolejnych pomysłów, z których pierwszym była idea Platona, że planety poruszają się ruchem jednostajnym po okręgach. Następnie Eudoksos i Arystoteles wymyślili układ współśrodkowych sfer z Ziemią w ich centrum, Apoloniusz przesunął Ziemię nieco w bok i wpadł na koncept deferentów i epicykli, zaś Hipparch na podstawie historycznych danych stworzył matematyczny opis ruchów Słońca i Księżyca. Ptolemeusz poprawił model Hipparcha i rozszerzył go na pozostałe planety wprowadzając dodatkowo ekwant. Mimo że koncepcja samego ekwantu stała w sprzeczności z filozofią Arystotelesa, całość modelu Ptolemeusza była głęboko w niej zanurzona. Chodzi tu szczególnie o podział Wszechświata na dwie rozłączne części, w których obowiązują odmienne prawa: świat podksiężycowy i obszar niebios.
Można się zastanawiać, co by się stało, gdyby arystotelizm nie zdominował myślenia większości greckich astronomów. Może zwrócono by wtedy większą uwagę na koncepcje Arystarcha i znaleźliby się jego następcy, którzy doprowadziliby do powstania matematycznego modelu ze Słońcem w środku układu? Nie jest to chyba nieprawdopodobne, ale są to rozważania typu „co by było, gdyby...”, z których w sumie wynika niewiele.
Zauważmy jeszcze, że od momentu rzucenia przez Platona wyzwania, by astronomowie stworzyli matematyczny opis Wszechświata, do chwili pełnego (choć błędnego) rozwiązania tego problemu przez Ptolemeusza upłynęło aż pięć wieków – czyli tyle samo, ile nas dzieli od epoki Kopernika. Niech mi teraz ktoś powie, że obecna nauka rozwija się wolno!
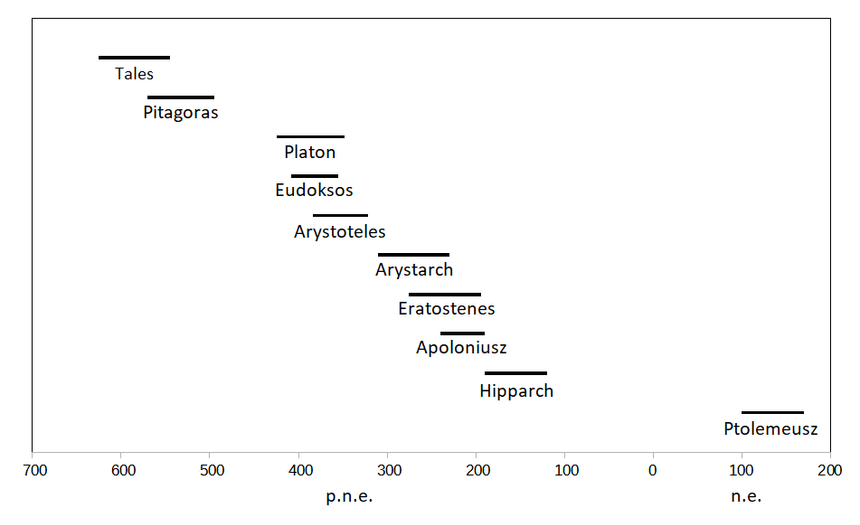
Chronologia greckich uczonych mających wpływ na rozwój astronomii
Ciąg dalszy nastąpi.
PS. Bibliografia (specjalnie dla kolegi blogera @eCitizen, żeby przestał jojczyć):
Hoskin, M. (red.) Historia astronomii
Kopernik, M. O obrotach ciał niebieskich i inne pisma (z obszernym wprowadzeniem L.A. Birkenmajera)
Ptolemeusz, K. Almagest (tłumaczenie angielskie)
Ptolemeusz, K. Hipotezy planetarne (tłumaczenie angielskie księgi I części A)
Wróblewski, A.K. Historia fizyki
oraz wiele, wiele artykułów w necie.
Sześć praw kierdela o dyskusjach w internecie: 1. Gdy rozum śpi, budzą się wyzwiska. 2. Trollem się nie jest; trollem się bywa. 3. Im mniej argumentów na poparcie jakiejś tezy, tym bardziej jest ona „oczywista”. 4. Obiektywny tekst to taki, którego wymowa jest zgodna z własnymi poglądami. 5. Dyskusja jest tym bardziej zawzięta, im mniej istotny jest jej temat. 6. Trzecie prawo dynamiki Newtona w ujęciu internetowym: każdy sensowny tekst wywołuje bezsensowny krytycyzm, a stopień bezsensowności krytyki jest równy stopniowi sensowności tekstu.
Nowości od blogera
Inne tematy w dziale Technologie

