Dlaczego Kopernik stworzył system heliocentryczny? 3. Ku astronomii predyktywnej

Jest to trzecia notka z serii; przed przeczytaniem prosiłbym o zapoznanie się z poprzednimi:

Dlaczego Kopernik stworzył system heliocentryczny?

Dlaczego Kopernik stworzył system heliocentryczny? 2. Reakcje na wyzwanie Platona

Dalszy rozwój astronomii starożytnej polegał w zasadzie na ulepszaniu i modyfikowaniu modelu Eudoksosa-Arystotelesa. Znaleźli się jednak uczeni, którzy go kwestionowali. Heraklides z Pontu (ok. 390–ok. 310 p.n.e.) uważał co prawda, że środkiem Wszechświata jest Ziemia, ale kręci się ona z zachodu na wschód, a my widzimy to jako dobowy ruch sfery niebieskiej. Jeszcze dalej poszedł Arystarch z Samos (ok. 310–ok. 230 p.n.e.). On z kolei twierdził, że środkiem Wszechświata jest Słońce, a Ziemia obiega je po okręgu. Ponieważ zachowało się jedynie krótkie omówienie oryginalnej pracy Arystarcha, które Archimedes zamieścił w jednym ze swych dzieł, szczegóły tego modelu nie są niestety znane.

Większość uczonych skłaniała się jednak ku nieruchomej Ziemi. Przemawiały za tym przesłanki nie tylko filozoficzne, ale i doświadczalne. Starożytni nie znali jeszcze zasady względności ruchu, więc przekonywał ich argument, który na pozór trudno podważyć. Gdy zrzucimy kamień z wysokiej wieży, spadnie koło jej podstawy. Jeżeli łucznik wystrzeli strzałę pionowo w górę, to po chwili upadnie ona tuż obok niego. A przecież, gdyby Ziemia się obracała, w trakcie lotu kamienia czy strzały powinna się nieco przesunąć. Kamień spadłby więc w pewnej odległości od wieży, a strzała w pewnej odległości od łucznika. Tego efektu wszakże nie obserwujemy. Ergo – to Ziemia jest nieruchoma, a ciała niebieskie kręcą się wokół niej!

Innym argumentem przemawiającym na niekorzyść ruchu Ziemi był brak obserwowanego efektu paralaksy gwiazd. Jeżeli Ziemia obiega Słońce, to gwiazdy powinniśmy widzieć pod coraz to innym kątem, a zatem musiałyby one zmieniać swe widome położenia w rocznym cyklu. Arystarch uważał, że gwiazdy są zbyt daleko od nas, aby efekt ten był dostrzegalny, ale inni astronomowie greccy nie zaakceptowali takiego wyjaśnienia. Dziś wiemy, że to Arystarch miał rację: paralaksa gwiazd jest tak mała, że udało się ją wyznaczyć dopiero w XIX wieku, a żeby tego dokonać, do pomiarów trzeba było użyć silnych teleskopów.

Model Eudoksosa-Arystotelesa był jednak krytykowany z innych powodów; mianowicie, nie potrafił on wytłumaczyć obserwowanych zmian jasności planet. Dla przykładu, Mars przez większość czasu jest dość słaby, ale raz na kilka lat staje się jednym z najjaśniejszych obiektów na niebie. Astronomowie greccy słusznie interpretowali te zmiany jako następstwo zmian odległości planet od Ziemi. W modelu Eudoksosa-Arystotelesa odległość każdej planety jest stała i zmiany jasności nie powinny występować.

Z problemem tym poradził sobie Apoloniusz z Pergi (ok. 240–ok. 190 p.n.e.). Ten matematyk i astronom, o którego życiu wiemy niewiele, znany jest głównie z odkrycia krzywych stożkowych: elipsy, paraboli i hiperboli. Chcąc wytłumaczyć zmiany jasności planet, przyczynił się jednak także do rozwoju modelu geocentrycznego wprowadzając doń dwie istotne modyfikacje.

Pierwsza modyfikacja jest stosunkowo prosta, a polega na przesunięciu Ziemi z centrum współśrodkowych sfer nieco w bok. Planeta nadal porusza się ruchem jednostajnym, ale ponieważ nie znajdujemy się w środku sfery, jej odległość od nas się zmienia.

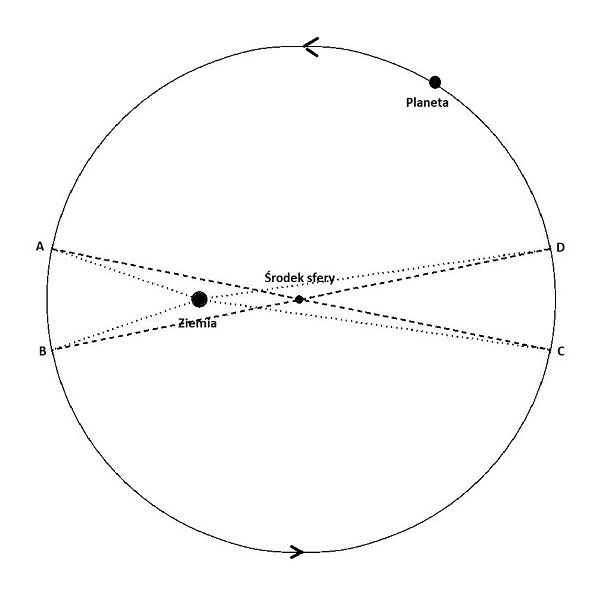
Mimośrodowy model ruchu planety Apoloniusza

W tym „mimośrodowym” modelu zmienna jest także obserwowana z Ziemi prędkość kątowa ciała niebieskiego na tle gwiazd. Przyjrzyjmy się powyższemu rysunkowi. Planeta przyczepiona jest do sfery obracającej się z jednostajną prędkością wokół osi przechodzącej przez jej środek. Przyjmijmy, że długość łuku AB jest równa długości łuku CD. Skoro tak, czas pokonania łuku AB przez planetę jest taki sam jak czas przesunięcia się z punktu C do punktu D. Ale dla obserwatora z Ziemi, która jest odsunięta od środka sfery, łuk AB stanowi większy kąt niż łuk CD. A zatem, dla nas Ziemian planeta ma większą prędkość kątową poruszając się od A do B, niż wtedy, gdy porusza się od C do D.

Efekt ten może tłumaczyć zmienną prędkość Słońca na sferze niebieskiej. Jej skutkiem jest różna długość pór roku. Słońce przebywa nad półkulą północną Ziemi dłużej niż nad półkulą południową, dzięki czemu wiosna i lato są u nas dłuższe od jesieni i zimy w sumie o siedem i pół dnia (co mnie osobiście bardzo cieszy).

Mimośrodowe położenie Ziemi nie jest jednak w stanie wyjaśnić pętli kreślonych przez planety. Z tego powodu Apoloniusz zaproponował drugi model, w którym planeta porusza się ruchem jednostajnym po okręgu zwanym epicyklem; z kolei środek tego okręgu przesuwa się wokół Ziemi, też ruchem jednostajnym, po innym okręgu – deferencie.

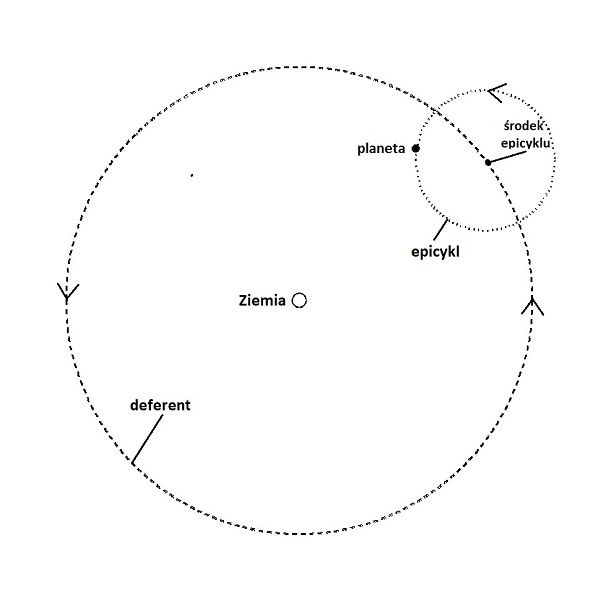
Model ruchu planety z deferentem i epicyklem

W modelu tym zmienia się odległość planety od Ziemi, a jeśli promienie i prędkości ruchów po deferencie i epicyklu są odpowiednio dobrane, planeta może na niebie zakreślać pętle. Jeżeli wierzymy w realne istnienie przezroczystych sfer, epicykl należy utożsamić z równikiem takiej sfery. O ile zajdzie taka potrzeba, do głównego epicyklu można doczepiać kolejne epicykle – kolejne sfery.

Zwróćmy uwagę na istotną różnicę między modelem Eudoksosa-Arystotelesa i deferentowo-epicyklowym modelem Apoloniusza. W tym pierwszym sfery planetarne otaczają Ziemię, podczas gdy w drugim sfery-epicykle krążą wokół Ziemi.

Nie wiadomo, jak daleko Apoloniusz rozwinął swój model epicykli i deferentów, gdyż jego pisma astronomiczne zaginęły. Patrząc z perspektywy wielu wieków mamy do czynienia ze swoistym paradoksem. Deferenty i epicykle, które wymyślił Apoloniusz chcąc stworzyć opis prawdziwego ruchu planet, już dawno odeszły w niebyt. W rzeczywistości ciała niebieskie poruszają się po krzywych stożkowych, które Apoloniusza interesowały z czysto matematycznego punktu widzenia...

Wszystkie opisane dotychczas modele miały charakter czysto jakościowy i nie można było wykorzystywać ich do przewidywania zjawisk na niebie. Przełom nastąpił dzięki Hipparchowi (ok. 190–ok. 120 p.n.e.). Hipparch, który większą część życia spędził na wyspie Rodos, był jednym z największych uczonych Starożytności. Tego astronoma i matematyka można uznać za prekursora trygonometrii, bo choć nie używał jeszcze funkcji trygonometrycznych (sinusy i cosinusy wymyślili dopiero Hindusi w VI wieku n.e.), to opracował tablice długości cięciw łuków dla różnych kątów. Stworzył katalog ponad tysiąca gwiazd i wprowadził stosowany do dzisiaj sposób oceny ich jasności za pomocą tak zwanych wielkości gwiazdowych. To dzięki niemu używamy sformułowania „gwiazda pierwszej wielkości” na określenie kogoś, kto wyróżnia się w swojej dziedzinie. Zmierzył odległość Księżyca od Ziemi, zaproponował metodę określania długości geograficznych za pomocą zaćmień Księżyca (patrz moja notka Jaka jest twoja długość?) i dokonał wielu innych pomiarów i odkryć, ale dla naszej historii najważniejszy jest jego model ruchów Słońca i Księżyca.

Hipparch w jakiś sposób wszedł w posiadanie danych o zaćmieniach, które Babilończycy zbierali w celach astrologicznych przez wiele setek lat. Jak na owe czasy były one niezwykle precyzyjne. Dzięki temu zestawowi danych mógł obliczyć dokładne położenia Słońca i Księżyca w przeszłości – zaćmienia występują przecież wtedy, gdy te ciała niebieskie są ustawione w określony sposób względem Ziemi. To z kolei pozwoliło Hipparchowi na stworzenie matematycznego opisu ich ruchów. Do opisu ruchu Słońca posłużył mu mimośrodowy model Apoloniusza, zaś dla Księżyca – model z deferentem i epicyklem. Hipparch w sprytny sposób wyznaczył promienie deferentu i epicyklu, a także prędkości, z jakimi poruszał się po nich Księżyc. Dzięki modelowi Hipparcha można było w końcu precyzyjnie przewidywać czasy przyszłych zaćmień.

Jak widać, już w Starożytności w rozwiązywaniu problemów naukowych przydatna była stosowana dziś powszechnie strategia, która polega na żmudnym gromadzeniu danych i nawiązywaniu współpracy międzynarodowej – w tym przypadku grecko-babilońskiej.

Ciąg dalszy nastąpi.