Poniższa notka nie stanowi odrębnej całości, ale jest integralną częścią cyklu o historii wyznaczania współrzędnych geograficznych. Jeżeli jakiś punkt wydaje się niezrozumiały, istnieje duże prawdopodobieństwo, że został wytłumaczony w którymś z wcześniejszych tekstów. Aby przeczytać całość, lekturę należy zacząć od Jakie jest twoje miejsce na Ziemi?, po czym posuwać się zgodnie z linkami zamieszczanymi na końcu każdej kolejnej notki.
W poprzednim tekście opisano sposób wyznaczania różnicy długości geograficznych za pomocą pomiarów odległości księżycowych gwiazd. Inną, równie wizjonerską, a jednocześnie znacznie mniej skomplikowaną metodę wymyślił niderlandzki kartograf Gemma Frisius (którego parę razy już wspominałem). W 1530 roku przedstawił sposób, w jaki do pomiaru długości można wykorzystywać zegary. Kapitan albo nawigator nastawiałby zegar na lokalny czas portu wypłynięcia, a w trakcie podróży porównywał ten czas z aktualnym czasem na statku (który można wyznaczać metodami astronomicznymi). Różnica tych czasów dawałaby różnicę długości geograficznych portu i pozycji statku na morzu. Proste, nieprawdaż?
Prawdaż, tyle tylko, że w czasach Frisiusa najlepsze zegary mechaniczne spieszyły się bądź spóźniały nawet o 15 minut na dobę, a nikt wtedy nie wiedział, jak można by poprawić ich chód. Łatwo obliczyć, że niedokładność równa 15 minutom czasowym przekłada się na błąd w położeniu wynoszący nawet kilkaset kilometrów… Tak więc metodę Frisiusa trzeba było odłożyć na półkę i czekać, aż ktoś wynajdzie wystarczająco precyzyjny czasomierz.
Jeszcze inną metodą miało być wykorzystanie kompasów magnetycznych. Z tego urządzenia nawigacyjnego korzystano w Europie od końca XII wieku. Początkowo sądzono, że igła kompasu dokładnie wskazuje na biegun północny Ziemi, jednakże w XVI wieku zdawano już sobie sprawę, iż nie jest to prawdą: faktycznie igła zwraca się ku biegunowi magnetycznemu, który leży dość blisko bieguna geograficznego, ale nie jest z nim tożsamy. Kąt między kierunkiem na biegun geograficzny a kierunkiem na biegun magnetyczny nosi nazwę deklinacji magnetycznej (której rzecz jasna nie należy mylić z deklinacją – współrzędną na sferze niebieskiej). Wybitny kartograf flamandzki, Gerardus Mercator (1512-1594), dzisiaj znany głównie z tak zwanego rzutu Mercatora, za pomocą którego tworzone są mapy całej Ziemi, zauważył, że to właśnie deklinacja magnetyczna być może stanowi klucz do określania współrzędnych geograficznych na morzu.
Metodę tę Mercator wyłożył w swym epokowym dziele "Nowe i pełniejsze przedstawienie ziemskiego globu odpowiednio zaadaptowane do celów nawigacyjnych", opublikowanym w 1569 roku. Gdyby udało się stworzyć mapę deklinacji magnetycznej, mogłaby ona służyć do wyznaczania pozycji statków. Nawigatorzy sposobami astronomicznymi określaliby kierunek na biegun geograficzny i porównywali z kierunkiem wskazywanym przez kompas; kąt między tymi kierunkami dawałby wartość lokalnej deklinacji magnetycznej. Następnie należało poszukać na mapie miejsca, gdzie deklinacja magnetyczna ma taką właśnie wartość, i sprawa załatwiona. Zaletą stosowania metody deklinacji magnetycznej byłby brak konieczności precyzyjnego pomiaru czasu, natomiast wadą – konieczność stworzenia kompletnych map oceanów.
A zatem, w XVI wieku sytuacja wyglądała następująco. Uczeni zaproponowali trzy różne metody wyznaczania długości geograficznej: odległości księżycowe, dokładny pomiar czasu i wykorzystanie deklinacji magnetycznej. Wszystkie te koncepcje wydawały się poprawne, ale ówczesny poziom technologii nie pozwalał na ich realizację. Dlatego, aby przezwyciężyć impas, władcy państw uczestniczących w dalekomorskich wyprawach ustanawiali ogromne nagrody pieniężne przeznaczone dla tych, co rozwiążą problem długości.
* * *
Na początku XVII wieku pojawił się w Europie wynalazek, który pomógł rozwiązać część omawianych wcześniej problemów. Niderlandzcy optycy stworzyli instrument, który pozwalał „widzieć odległe rzeczy tak, jakby były blisko” – czyli teleskop. O wynalazku usłyszał Galileo Galilei (1564-1642), po naszemu Galileusz, i skonstruował własną wersję tego urządzenia, po czym jako pierwszy skierował je na niebo. Za jego pomocą odkrył niesamowite, nieznane wcześniej rzeczy: góry i kratery na Księżycu, fazy Wenus, plamy na Słońcu i wiele gwiazd, których nie widać gołym okiem. Te obserwacje zmieniły całą ludzką wiedzę o Wszechświecie, dla nas jednak ważne będzie inne jego odkrycie.
W nocy 7 stycznia 1610 roku Galileusz skierował swoją lunetę na Jowisza. Dostrzegł tarczę planety, a obok niej trzy jasne gwiazdy. Przez następne kilka nocy uczony kontynuował obserwacje i stwierdził, że te cztery gwiazdy (odkrył bowiem także czwartą) cały czas znajdowały się blisko Jowisza, choć ich konfiguracja stale ulegała zmianom. Zdarzało się, że któraś z tych gwiazd znikała za planetą. Wniosek mógł być tylko jeden: zauważone obiekty to nie gwiazdy, ale satelity Jowisza, razem z nim pędzące w przestrzeni.

Jowisz i Księżyce Galileuszowe widziane przez amatorski teleskop (fot. Jan Sandberg, wiki; no commercial use)
Galileusz, jak każdy wykształcony Europejczyk żyjący w owej epoce, wiedział o problemie długości geograficznej (i o nagrodach za jego rozwiązanie). Wpadł na pomysł, jak do tego celu wykorzystać swoje odkrycie. Zjawisko zaćmień Księżyców Galileuszowych (ich znikanie za tarczą Jowisza) możne posłużyć do wyznaczania długości tak samo, jak zaćmienia Księżyca: należy porównać lokalny czas tego zdarzenia z czasem przewidzianym dla jakiegoś konkretnego miejsca. Ponieważ jednak Księżyce Galileuszowe okrążają Jowisza stosunkowo szybko – okresy ich obiegów wynoszą od kilkudziesięciu do kilkuset godzin – ich zaćmienia zdarzają się znacznie częściej niż zaćmienia naszego Księżyca. Można więc dokonywać pomiarów co kilka dni (a nie raz na rok).
W 1612 roku Galileusz przedstawił swój pomysł królowi Hiszpanii Filipowi III, który 14 lat wcześniej ustanowił wysoką dożywotnią pensję jako nagrodę dla tego, kto znajdzie sposób określania długości. Komisja uznała jednak, że nagrodę przyzna uczonemu dopiero wtedy, gdy ten zademonstruje użyteczność swojej koncepcji w praktyce.
Największą bolączką metody Galileusza była trudność obserwacji Jowisza z pokładu chybocącego się statku. Galileusz wymyślił więc sprytne urządzenie, które nazwał celatone. Miało ono umożliwić wykonywanie tej czynności. Był to hełm z dwoma otworami na oczy. Jeden otwór był otwarty, natomiast do drugiego przymocowano lunetkę. Nawigator miał gołym okiem lokalizować Jowisza na niebie, natomiast drugim – tym uzbrojonym w lunetkę – obserwować księżyce planety.

Współczesna rekonstrukcja celatone (fot. Museo Galileo, wiki; CC license)
Wiosną 1617 roku Galileusz próbował użyć celatone stojąc na pokładzie statku w porcie w Livorno. Niestety, kołysanie statku uniemożliwiło mu dostrzeżenie księżyców Jowisza. Kolejną próbę podjął we wrześniu tego roku, tym razem umieszczając siebie na wiszącej platformie. Mimo że już dobrze widział niebo, komisja znowu odrzuciła jego pomysł twierdząc, iż obserwacje nie były wystarczająco dokładne.
Galileusz powrócił do celatone prawie 20 lat później, usiłując wcisnąć swój wynalazek Stanom Generalnym Niderlandów (które też oferowały wysoką nagrodę odkrywcy metody pomiaru długości geograficznej). Tym razem przedstawił konstrukcję składającą się z dwóch półkul. W wykonanej z brązu półkuli wewnętrznej miał siedzieć obserwator z celatone. Półkula ta umieszczona była w półkuli zewnętrznej, a między nimi znajdowała się warstwa oleju. Taki układ miał zapewniać stabilność nawigatora nawet na wzburzonym morzu. Admirał floty holenderskiej odrzucił jednak ten projekt, gdyż uznał, że marynarze „to prości ludzie, którzy tylko powierzchownie znają się na astronomii i matematyce”, i dlatego nie będą potrafili stosować metody Księżyców Galileuszowych w codziennej żegludze. Mimo to, za wysiłki, jakie Galileusz podjął w celu rozwiązania problemu długości, dwór holenderski postanowił uhonorować go czymś w rodzaju nagrody pocieszenia w postaci złotego łańcucha; Galileusz tę nagrodę z niesmakiem odrzucił.
Pomysł wykorzystania Księżyców Galileuszowych w nawigacji dalekomorskiej okazał się więc bezużyteczny, ale można było z niego korzystać na lądzie obserwując Jowisza przez stabilnie ustawione teleskopy. W 2. połowie XVII wieku powstała we Francji Królewska Akademia Nauk, a przy niej Obserwatorium Paryskie, którego dyrektorem został ściągnięty z Włoch astronom Jean-Dominique Cassini (1625-1712). Jednym z głównych zadań Akademii było stworzenie dokładnej mapy Francji. Dla określania długości stosowano metodę Księżyców Galileuszowych. Szybko okazało się, że poprzednie mapy obarczone były błędem: atlantyckie wybrzeże tego kraju wysuwano za bardzo na zachód. W rezultacie powierzchnia Francji była mniejsza niż wcześniej sądzono. Podobno Ludwik XIV, gdy mu pokazano nową mapę, miał powiedzieć, że uczeni odebrali mu więcej terytorium niż stracił we wszystkich przegranych wojnach.
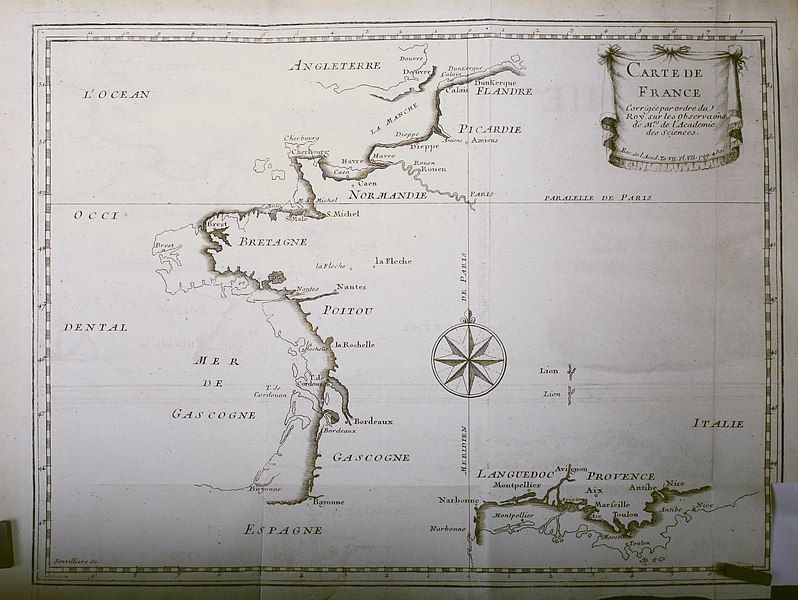
Wyznaczony w 1684 roku kształt wybrzeża Francji (gruba linia) nałożony na starszą mapę (cienka linia) (wiki; public domain)
Innym zadaniem, jakiego podjęli się francuscy astronomowie, był pomiar różnicy długości między Paryżem a duńską wyspą Hven. Na wyspie tej w 2. połowie XVI wieku miał swoje obserwatorium znakomity uczony Tycho Brahe (1546-1601). Zostawił on po sobie potężną ilość danych obserwacyjnych, ale żeby je powiązać z późniejszymi o wiek obserwacjami w Paryżu, trzeba było wyznaczyć różnicę długości obu obserwatoriów. Cassini wysłał grupę astronomów pod kierownictwem Jean-Félixa Picarda na Hven, gdzie obserwowali księżyce Jowisza, a on sam prowadził takie obserwacje w Paryżu. Następnie porównano wyniki i w ten sposób poznano dokładną różnicę długości geograficznych między Hven a Paryżem.
Do grupy kierowanej przez Picarda należał Duńczyk Ole Rømer (1644-1710). Przyglądając się Księżycom Galileuszowym zauważył ciekawe zjawisko. Gdy Jowisz znajduje się stosunkowo blisko Ziemi, zaćmienia następują wcześniej niż wtedy, gdy jest bardziej oddalony. Rømer słusznie zinterpretował ten fakt skończoną prędkością światła: kiedy planeta jest dalej, światło musi przebyć dłuższą drogę i dociera do nas później. Było to jedno z najważniejszych odkryć w historii nauki. Skończona prędkość światła stanowi dziś jedną z podstaw fizyki i astronomii.
O odkryciu Rømera słyszał pewnie każdy, kto interesuje się historią nauki, ale nie wiem, czy wszyscy zdają sobie sprawę, że był to niejako produkt uboczny walki o znalezienie metody wyznaczania długości geograficznej. Takich ważnych „produktów ubocznych” było zresztą więcej. Pojawią się one w dalszej części cyklu.
Ciąg dalszy nastąpi.
Sześć praw kierdela o dyskusjach w internecie: 1. Gdy rozum śpi, budzą się wyzwiska. 2. Trollem się nie jest; trollem się bywa. 3. Im mniej argumentów na poparcie jakiejś tezy, tym bardziej jest ona „oczywista”. 4. Obiektywny tekst to taki, którego wymowa jest zgodna z własnymi poglądami. 5. Dyskusja jest tym bardziej zawzięta, im mniej istotny jest jej temat. 6. Trzecie prawo dynamiki Newtona w ujęciu internetowym: każdy sensowny tekst wywołuje bezsensowny krytycyzm, a stopień bezsensowności krytyki jest równy stopniowi sensowności tekstu.
Nowości od blogera
Inne tematy w dziale Technologie

