Jakie jest twoje miejsce na Ziemi? Część 2.

W poprzedniej notce opisałem, jak mierzy się szerokość geograficzną w nocy korzystając z Gwiazdy Polarnej. Wartość tę można otrzymać także w dzień za pomocą Słońca. Co prawda w ciągu roku Słońce zmienia swoje położenie względem równika i gwiazd: w dzień przesilenia letniego znajduje się najdalej na północ od równika niebieskiego, a w dzień przesilenia zimowego – najdalej w kierunku południowym, ale nie stanowi to żadnego problemu, gdyż już od czasów starożytnych znane były tabele jego pozycji na sferze niebieskiej, podawane na każdy dzień.

Pozycje Słońca (a także innych ciał niebieskich) na sferze niebieskiej przedstawia się w postaci dwóch liczb w jednym z kilku stosowanych układów współrzędnych. Najwygodniejszy układ nosi mądrą nazwę układu współrzędnych równikowych równonocnych. Jedna z występujących w nim liczb, deklinacja (oznaczana zwykle grecką literą δ), odpowiada ziemskiej szerokości geograficznej; jest to zatem kąt między prostą przechodzącą przez dany punkt na sferze niebieskiej i środek Ziemi (a praktycznie przez obserwatora) a płaszczyzną równika. Druga liczba, rektascensja (oznaczana jako α), jest odpowiednikiem długości geograficznej. A zatem w tabelach można znaleźć deklinację i rektascensję Słońca na każdy dzień roku.

Szerokość geograficzną wyznaczać należy wtedy, gdy Słońce znajduje się najwyżej na niebie, czyli w południe, gdyż oznacza to, że w tym momencie przechodzi przez południk. Położenie Słońca względem horyzontu zależy od jego deklinacji oraz punktu obserwacji. Dla przykładu, w sytuacji gdy wartość deklinacji Słońca δ jest mniejsza od szerokości geograficznej φ obserwatora, południk wygląda tak:

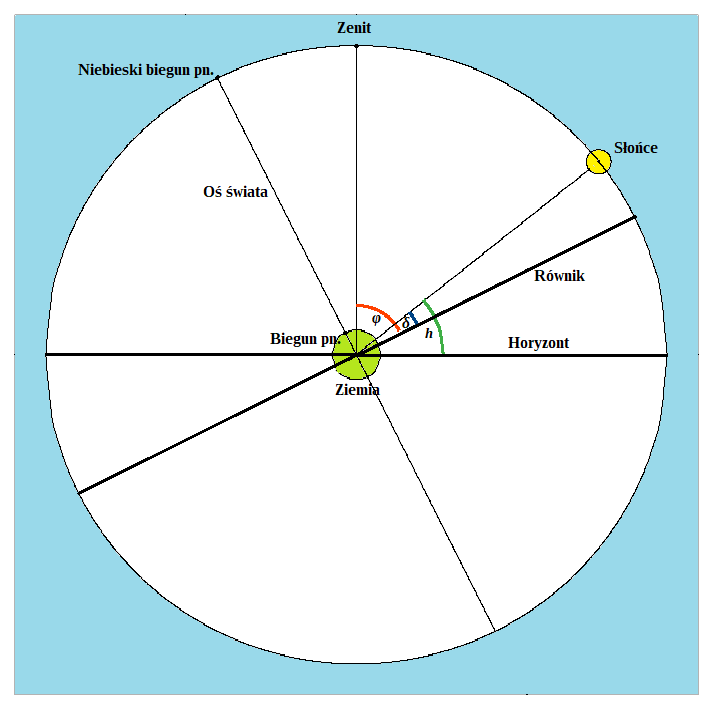
Żeby nie komplikować rysunku, na ilustracji horyzont nie jest styczny do powierzchni Ziemi, ale przechodzi przez jej środek. Nie powoduje to błędu, gdyż, jako się rzekło, rozmiar naszej planety (tu narysowanej przesadnie dużej) jest zaniedbywalnie mały w porównaniu z odległościami do ciał niebieskich, w tym także do Słońca. Z rysunku widać natychmiast, że kąt będący dopełnieniem do kąta prostego wysokości Słońca nad horyzontem h (czyli kąt 90^o−h) jest równy różnicy wartości szerokości geograficznej obserwatora φ i deklinacji Słońca δ. Stąd mamy wzór na szerokość geograficzną: φ = 90^o+δ−h.

Wyznaczanie szerokości geograficznej za pomocą Słońca przebiega zatem następująco. W okolicy południa mierzymy zmieniającą się kątową wysokość Słońca nad horyzontem, która najpierw rośnie, a potem maleje. Największa wysokość przypada w momencie, gdy Słońce przechodzi przez nasz południk. Jest to właśnie poszukiwana przez nas wartość h. Znając z tabel wartość deklinacji Słońca δ przypadającą na dzień wykonywania pomiaru, ze wzoru obliczamy szerokość geograficzną miejsca obserwacji.

Dokładność wyznaczenia szerokości geograficznej zależy od precyzji pomiaru wysokości kątowej – czy to Gwiazdy Polarnej, czy też Słońca. Na stałym lądzie wysokość Słońca zasadniczo można wyznaczyć metodą zastosowaną przez Eratostenesa (którą opisałem w notce Jak zmierzono Ziemię?), czyli poprzez pomiar długości cienia rzucanego w południe przez pionową tyczkę. Niestety, sposób ten zawodzi na morzu, gdyż statki lubią się gibać, i dlatego cienie rzucane na pokład są bardzo niestabilne. Trzeba więc było wymyślić coś innego.

W dawnych wiekach do pomiaru kątów na niebie stosowano przeróżne urządzenia. Często używano kwadrantów, nazwanych tak, gdyż obejmowały zakres jednej czwartej koła. Najbardziej wyrafinowanym przyrządem było astrolabium. Znane już w Starożytności, jego wynalezienie przypisuje się bądź to Apoloniuszowi z Pergi (ok. 260-ok. 190 p.n.e.), bądź też Hipparchowi (ok. 190-120 p.n.e.). Obaj greccy uczeni byli zarówno świetnymi astronomami, jak i matematykami, więc każda z tych wersji jest prawdopodobna. Astrolabium zostało mocno ulepszone w świecie islamskim i stamtąd trafiło do Europy chrześcijańskiej.

Astrolabium z Sułtanatu Mameluków, rok 1282, Muzeum Sztuki Tureckiej i Islamskiej w Stambule (fot. Mustafa-trit20, wiki, CC license)

Podobnie jak opisany w poprzedniej notce nokturnał, astrolabium to instrument obserwacyjny połączony z analogowym kalkulatorem. Zwykle wykonywano je z brązu. Listwa obracająca się wokół środka służyła do pomiaru wysokości ciał niebieskich nad horyzontem, zaś skale wygrawerowane po obu stronach urządzenia pozwalały przeprowadzać wielorakie obliczenia astronomiczne, a nawet wyznaczać aktualny czas.

Ze względu na materiał, a także na konieczność niezwykle precyzyjnego wygrawerowania skal, koszt astrolabiów był wysoki. Z tego powodu nawigatorzy statków często zaopatrywali się w uproszczoną wersję urządzenia, czyli w tak zwane astrolabium morskie. Nie można było na nim wykonywać wszystkich obliczeń, które umożliwiało zwykłe astrolabium, wystarczało ono jednak w zupełności do pomiaru wysokości ciał niebieskich nad horyzontem:

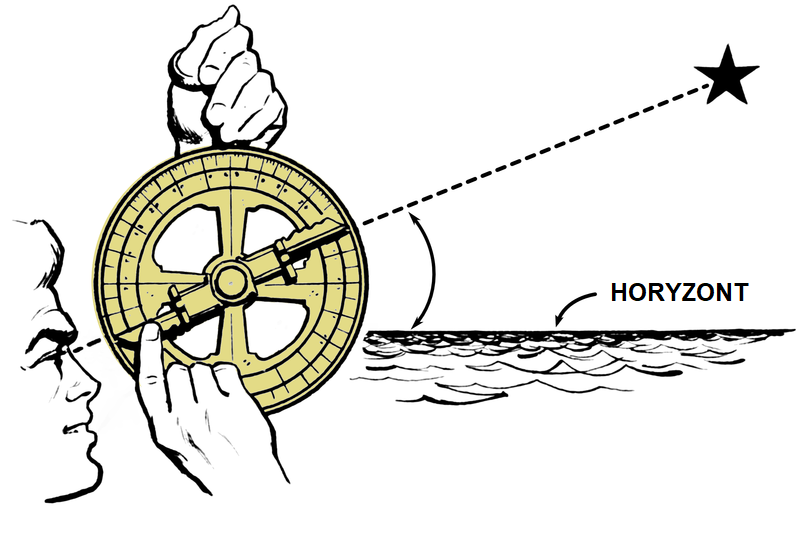
Pomiar wysokości gwiazdy nad horyzontem za pomocą astrolabium morskiego (rys. wiki, public domain)

Prostym, ale bardzo sprytnym przyrządem do pomiaru kątów była wymyślona w Średniowieczu laska Jakuba. Nie wiadomo, skąd wzięła się ta nazwa; według jednej z wersji nawiązuje ona do patrona pielgrzymów – świętego Jakuba. Opis laski Jakuba po raz pierwszy pojawił się w dziele żyjącego w Prowansji matematyka i astronoma Levi ben Gersona (1288-1344). Urządzenie składało się z dwóch prostopadłych do siebie listw, z których krótsza mogła być przesuwana wzdłuż dłuższej. Na dłuższej listwie narysowana była skala. Aby zmierzyć kąt między dwoma punktami, nawigator ustawiał poprzeczną listwę tak, żeby punkty te znajdowały się na jej końcach, po czym odczytywał wartość kąta ze skali. Laska Jakuba miała tę zaletę, że pozwalała mierzyć nie tylko wysokość nad horyzontem, ale i inne kąty na niebie i na Ziemi. Jej zastosowanie pokazuje rysunek umieszczony na okładce dzieła Petrusa Apianusa (1495-1552) pod tytułem Introductio geographica:

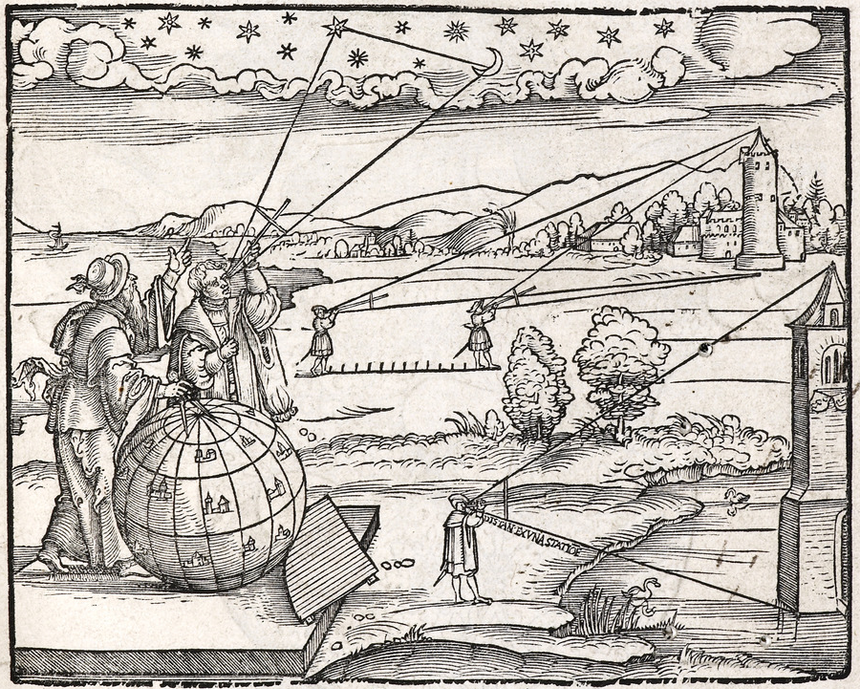
Pomiary różnych kątów za pomocą laski Jakuba

Poniższy filmik demonstruje, w jaki sposób za pomocą laski Jakuba mierzono wysokość Słońca:

Wczesne przyrządy do pomiaru kątów na niebie miały pewną szalenie istotną wadę: aby wyznaczyć wysokość Słońca nad horyzontem, trzeba było patrzeć na nie bezpośrednio. Wielokrotnie przeprowadzane pomiary musiały prowadzić do stopniowego pogarszania się wzroku, dlatego chorobą zawodową nawigatorów była ślepota. Z tego powodu stworzenie nowego rodzaju kwadrantu – kwadrantu Davisa – uznano za olbrzymie osiągnięcie. Wynalazca tego urządzenia, kapitan John Davis (ok. 1550-1605) był żeglarzem, który poszukiwał prowadzącej przez Arktykę północno-zachodniej drogi morskiej do Chin, odkrył Falklandy, bronił się przed fałszywymi oskarżeniami wysuwanymi przez kochanka swojej żony, a zginął zabity przez japońskich piratów. Zanim to jednak nastąpiło, zdążył skonstruować urządzenie, dzięki któremu nawigator mógł stać tyłem do Słońca i mierzyć cień rzucany przez pewien fragment instrumentu.

Jeszcze lepszym narzędziem stał się wymyślony w XVIII wieku sekstant. Dzięki skomplikowanemu połączeniu lunetki, lusterek i osłon przyciemniających można przez niego obserwować jednocześnie i horyzont, i Słońce (albo jakiś inny obiekt), a zamocowany kątomierz służy do odczytu kątów. Takie sekstanty są używane do dzisiaj przez tych, którzy nie lubią GPS-u lub chcą mieć jakąś niezależną alternatywę.