Jakie jest twoje miejsce na Ziemi?

Wyznaczanie swoich współrzędnych geograficznych to dzisiaj bułka z masłem: wystarczy posiadać smartfon i zainstalować na nim odpowiednią aplikację. Wokół naszej planety krąży flotylla kilkudziesięciu satelitów tworzących układ GPS (ang. Global Positioning System, czyli Ogólnoświatowy System Pozycjonowania). Sygnał z twojej komórki trafia do kilku z tych satelitów, a umieszczona na nich aparatura mierzy z nadzwyczajną precyzją czas jego nadejścia. Komputery systemu wykorzystują te dane i, dokonując obliczeń, w mgnieniu oka dokładnie określają twoje miejsce na Ziemi. Czy może być coś prostszego?...

Jednakże przez większość historii cywilizacji znalezienie metody dokładnego wyznaczania współrzędnych geograficznych stanowiło problem o kapitalnym wręcz znaczeniu. Nieumiejętność precyzyjnego określenia miejsca położenia, szczególnie na morzu, prowadziła do katastrof, w których masowo ginęli ludzie. Statki przepadały w bezkresie oceanów albo rozbijały się o ostre skały, które niespodziewanie wyrastały przed dziobem. Mniej więcej od połowy XV wieku, kiedy to rozpoczęła się epoka wypraw dalekomorskich, kwestia precyzyjnego określania swej aktualnej pozycji na naszym globie stała się naprawdę paląca. 

Długoletnie wysiłki znalezienia efektywnej metody wyznaczania współrzędnych geograficznych zaowocowały wieloma wynalazkami (z których część jest przydatna do teraz, zaś inne dzisiaj nas tylko śmieszą), a także nieoczekiwanymi odkryciami. Z problemem walczyli najwięksi geniusze naukowi Odrodzenia i Oświecenia: Galileusz, Huygens, Hooke, Newton, Halley, a także wielu innych. O ich zmaganiach pisze się rzadko, pewnie dlatego, że wszyscy oni ponieśli porażkę. Zwycięstwo udało się odnieść niepozornemu cieśli i dyrygentowi kościelnego chóru z wioski w północnej Anglii. Warto zapoznać się z fascynującą historią tej batalii. 

Wydaje się, że współrzędne geograficzne – szerokość i długość – jako pierwszy wprowadził Eratostenes (276-194 p.n.e.). To ten sam uczony, który jako pierwszy wyznaczył obwód Ziemi. Współrzędne pojawiają się w dziele Geographica, które niestety zaginęło, ale jego treść znamy z wykonanych później opisów. W XIX wieku udało się nawet odtworzyć umieszczoną w tym dziele mapę starożytnego świata:

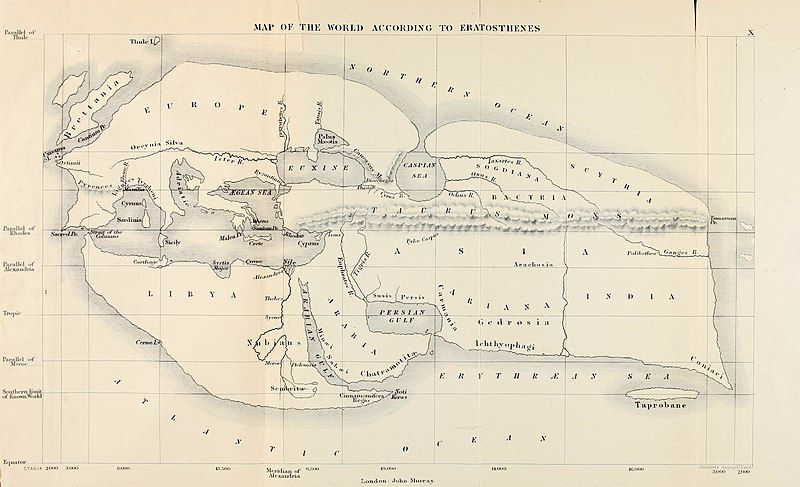
Rekonstrukcja mapy z Geographiki Eratostenesa

Podobieństwo mapy Eratostenesa do map dzisiejszych nie jest zbyt wielkie. Stosunkowo łatwo można rozpoznać kształt Morza Śródziemnego i Półwyspu Arabskiego, ale pozostałe obszary zupełnie nie przypominają realnej Ziemi. Pamiętajmy jednak, że była to pierwsza próba podsumowania ówczesnej wiedzy geograficznej, a samo wprowadzenie współrzędnych to osiągnięcie przełomowe. System współrzędnych geograficznych do dziś stanowi wygodny (i praktycznie jedyny) sposób określania miejsca na naszej planecie.

Jak zatem je wyznaczać? Zanim do tego przejdziemy, przypomnijmy sobie formalne definicje. Współrzędne geograficzne, czyli szerokość i długość, to dwa kąty na kuli ziemskiej, często oznaczane greckimi literami φ i λ.

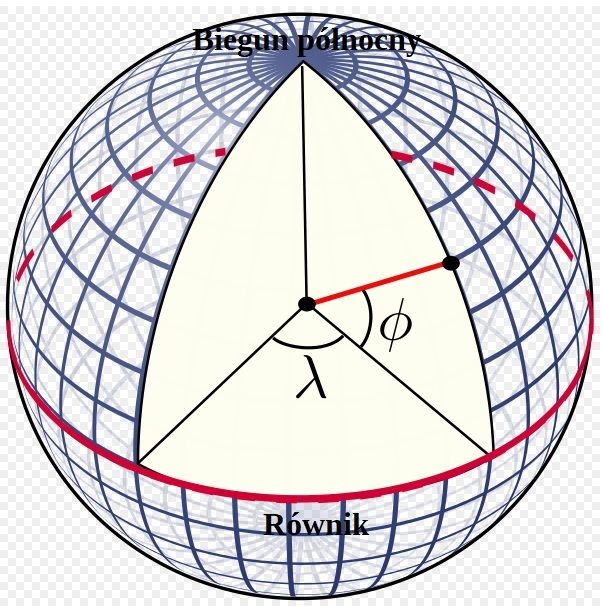
Współrzędne geograficzne (rys. wiki, free license)

Szerokość geograficzna danego punktu φ jest kątem między prostą przechodzącą przez ten punkt i środek Ziemi a płaszczyzną równika; z kolei długość geograficzna λ to kąt dwuścienny między płaszczyzną południka, na którym leży dany punkt, a innym, arbitralnie wybranym południkiem. Od ponad stu lat za południk referencyjny (południk „zerowy”) przyjmuje się południk przechodzący przez Greenwich w Anglii, wcześniej jednak dość dowolnie wybierano różne inne południki odniesienia.

Wyznaczanie szerokości geograficznej to procedura stosunkowo łatwa, przynajmniej w swej zasadzie. Przyjrzymy się płaszczyźnie południka niebieskiego, będącego rozciągnięciem południka ziemskiego aż do wyimaginowanej sfery niebieskiej. Łatwo zauważyć, że szerokość geograficzna konkretnego miejsca φ jest równa kątowi między pionem (kierunkiem na zenit) a równikiem, ale także między osią świata (przedłużeniem osi rotacji Ziemi aż do sfery niebieskiej) a równoległą do horyzontu płaszczyzną przechodzącą przez środek Ziemi.

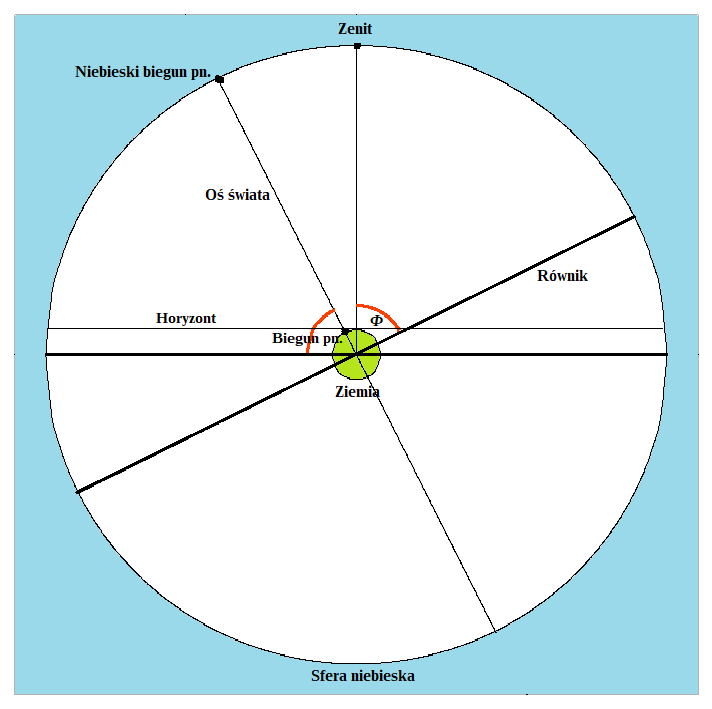
Południk niebieski

Ponieważ rozmiar Ziemi jest zaniedbywalnie mały w porównaniu z wielkością sfery niebieskiej (na ilustracji Ziemię pokazano przesadnie dużą), można przyjąć, że płaszczyzna ta pokrywa się z płaszczyzną horyzontu. Skoro tak, to wysokość kątowa bieguna niebieskiego (czyli punktu przecięcia osi świata ze sferą niebieską) nad horyzontem równa jest szerokości geograficznej danego miejsca. Należy zatem wyznaczyć tę wysokość.

Gdyby biegun niebieski był w jakiś szczególny sposób oznakowany – na przykład dokładnie na nim znajdowała się jakaś gwiazda – wyznaczenie szerokości geograficznej byłoby banalnie proste i sprowadzało się do pomiaru wysokości kątowej tejże gwiazdy. Niestety, takiej gwiazdy nie ma. Najbliższy jasny obiekt – Gwiazda Polarna – jest dzisiaj oddalona od bieguna o około ⅔ stopnia i w ciągu doby obiega go po kole o takim właśnie promieniu. (Oczywiście, jak świetnie wiemy od czasów Kopernika, to nie Gwiazda Polarna obiega biegun, lecz Ziemia kręci się z zachodu na wschód, a ruch wirowy naszej planety postrzegamy jako pozorny obrót sfery niebieskiej i znajdujących się na niej obiektów; często łatwiej jest jednak tłumaczyć pewne efekty przyjmując, tak jak czynili to starożytni, że nieruchoma jest Ziemia, a obraca się sfera niebieska). Wcześniej ta odległość była jeszcze większa. Według pomiaru przeprowadzonego przez niderlandzkiego kartografa Gemmę Frisiusa (o którym wspominałem już w jednej z wcześniejszych notek), w 1547 roku odległość Gwiazdy Polarnej od bieguna wynosiła nieco ponad 3 stopnie. Dlatego samo zmierzenie wysokości Gwiazdy Polarnej nad horyzontem nie wystarcza – należy wprowadzić jeszcze pewną poprawkę. Dla użytku morskich nawigatorów opracowano specjalne procedury obliczania poprawek pozwalających dokładnie określić szerokość geograficzną; nazywano je Regimentami Gwiazdy Polarnej. 

Wartość poprawki zależy zarówno od daty, jak i godziny, w której wykonuje się obserwację, trzeba więc mieć dobrą miarę czasu. Co prawda w późnym Średniowieczu pojawiły się już pierwsze zegary mechaniczne, jednakże ich chód nie był wystarczająco jednostajny, aby można je było stosować do celów astronomicznych. Na szczęście dla marynarzy natura dostarczyła im bardzo dokładny czasomierz: jest nim sama sfera niebieska. W ciągu doby dokonuje ona pełnego obrotu w kierunku ze wschodu na zachód, a jej ruch jest nadzwyczaj równomierny. 

Spójrzmy na okolice północnego bieguna nieba; wyglądają one mniej więcej tak:

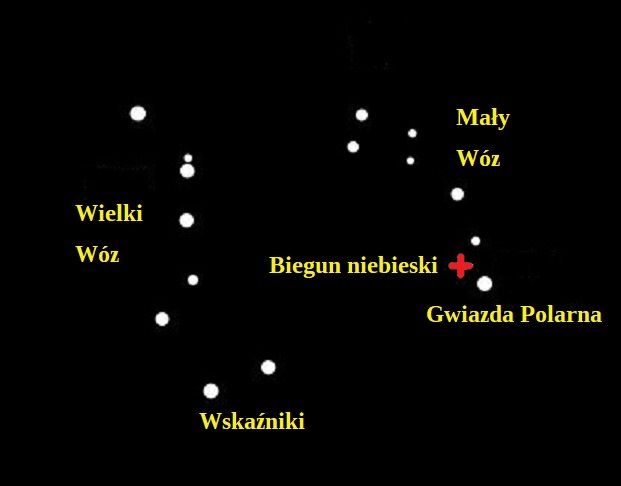
Okolice północnego bieguna nieba

Znajdują się tam dwa charakterystyczne asteryzmy: Wielki i Mały Wóz. Gwiazdy Wielkiego Wozu są bardzo jasne i bez problemu można je znaleźć na niebie. Gwiazdy Wozu Małego są nieco słabsze; dotyczy to także Gwiazdy Polarnej, którą niewprawnym oczom trudno czasem zidentyfikować. Leży ona jednak prawie dokładnie na przedłużeniu linii łączącej dwie tylne gwiazdy Wielkiego Wozu, które pomagają ją namierzyć (z tego powodu gwiazdy te nazywane są czasem Wskaźnikami).

Ponieważ sfera niebieska dokonuje obrotu wokół osi świata, położenie gwiazd na niebie stopniowo się zmienia:

Widok okolic północnego bieguna niebieskiego w odstępach sześciogodzinnych

A zatem gwiazdy (szczególnie te, które tworzą Wielki Wóz) mogą służyć jako wskazówki ogromnego kosmicznego zegara!

Aby na zegarze tym można było precyzyjnie odczytać czas, stworzono pomysłowe urządzenie nazwane nokturnałem. Był to instrument obserwacyjny połączony z analogowym kalkulatorem. Składał się z dwóch współosiowych okrągłych tarcz, wykonanych zwykle z drewna lub mosiądzu, do których dołączano jedną lub więcej wskazówek. Na zewnętrznym pierścieniu zaznaczano dni i miesiące, a na wewnętrznym – godziny.

Nokturnał (fot. Johann "nojhan" Dréo, wiki, CC license)

Obserwator najpierw ustawiał pierścienie w taki sposób, by północ znajdowała się przy odpowiedniej dacie, po czym, trzymając go pionowo, kierował go tak, by przez otwór w środku instrumentu widzieć Gwiazdę Polarną. Następnie obracał wskazówkę tak, by „dotykała” ona Wskaźników Wielkiego Wozu. Precyzyjny czas można było odczytać z przecięcia wskazówki z oznaczeniami godzinowymi na pierścieniu.

Zasadę działania nokturnału i sposób jego użycia pokazuje poniższy filmik:

Ciąg dalszy nastąpi.