Kształt Ziemi, Kartezjusz i Newton

Przed przeczytaniem tej notki proszę zapoznać się z Częścią 1, Częścią 2, Częścią 3, a już absolutnie koniecznie z Częścią 4!

Drodzy Czytelnicy, muszę uderzyć się w piersi – i to bardzo mocno. W poprzedniej części popełniłem aż dwa poważne błędy. Pierwszy spowodowany był nieuwzględnieniem pewnej geometrycznej własności elips, drugi – zbyt pobieżną lekturą.

Najpierw błąd pierwszy. Rysując elipsę, będącą przekrojem spłaszczonej bądź wydłużonej Ziemi, poprowadziłem linie pokazujące różne szerokości geograficzne do środka elipsy. Miały one pokazywać równe różnice między szerokościami geograficznymi:

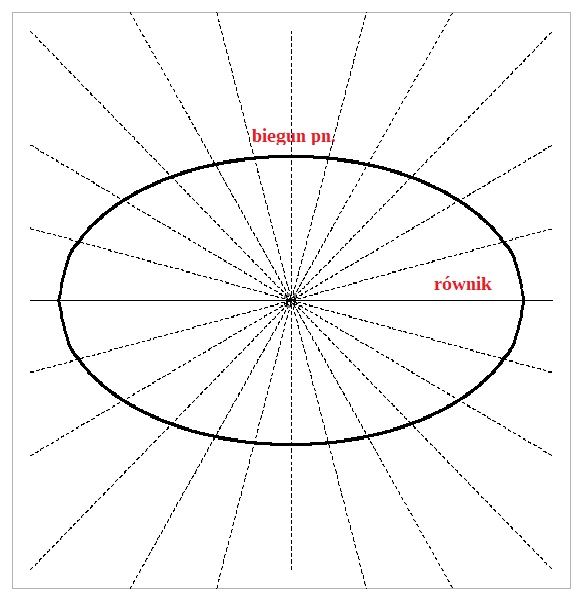
Ale w rzeczywistości astronomowie wyznaczają szerokość geograficzną nie poprzez pomiar kąta między prostą przechodzącą przez środek Ziemi a płaszczyzną równika – byłoby to nie do zrealizowania – lecz między kierunkiem lokalnego pionu a płaszczyzną równika. A jeśli Ziemia nie jest idealną kulą, to kierunek pionu nie pokrywa się z prostą przechodzącą przez środek Ziemi! Dlatego długość jednego stopnia łuku południka w przypadku spłaszczonej Ziemi jest większa w dużych szerokościach geograficznych niż w małych – przeciwnie niż napisałem w poprzedniej notce. I odwrotnie, w przypadku wydłużonej Ziemi długość łuku jest mniejsza w dużych szerokościach. Widać to dobrze na tej ilustracji:

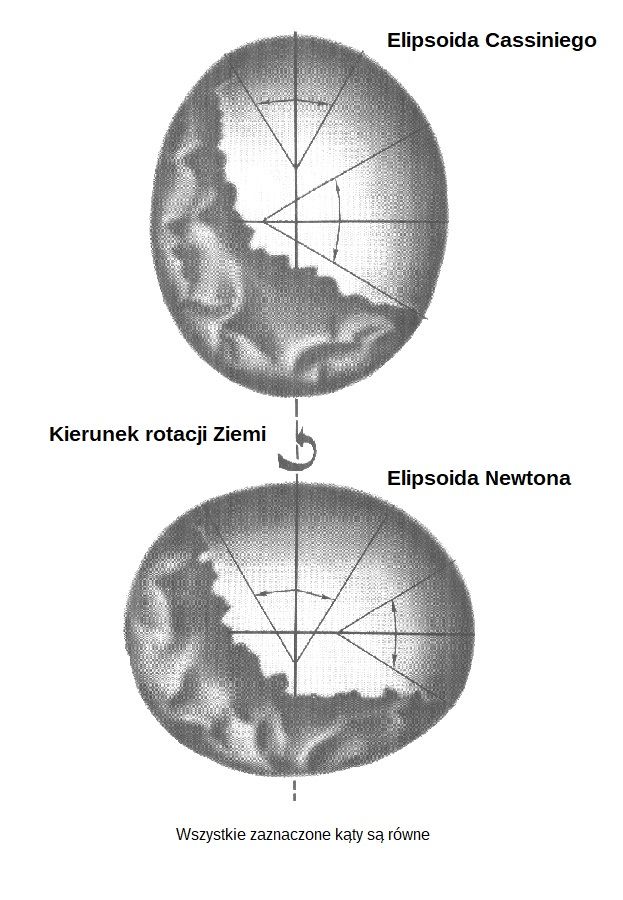
Drugi mój błąd wynikał ze zbyt pobieżnej lektury źródeł. Kiedy przeczytałem o pomiarach Cassiniego, automatycznie założyłem, że porównał swój wynik z wcześniejszym rezultatem Picarda. Faktycznie było inaczej: Cassini podzielił mierzony przez siebie łuk południka na dwie części: północną i południową. Wyszło mu, że część północna jest krótsza niż południowa, i stąd wyciągnął wniosek, iż Ziemia ma wydłużony kształt.

Ale wstyd... Mam nadzieję, że Czytelnicy mi to jednak wybaczą... 

Jeśli mimo moich błędów chcecie nadal to czytać, oto dalszy ciąg historii. Co prawda wynik Cassiniego sugerował, że Ziemia jest wydłużona, ale zdawano sobie sprawę, iż jego pomiary mogą być obarczone błędem. Dlatego Akademia Francuska postanowiła wysłać dwie ekspedycje do dwóch różnych zakątków świata: jednego w pobliżu równika, drugiego na dalekiej północy. Jak na owe czasy, koszty i trudności organizacji takich wypraw były olbrzymie. Myślę, że można je porównać do dzisiejszych problemów z wysłaniem ludzi na Księżyc. 

Szefem rozpoczętej w 1735 roku ekspedycji do dzisiejszego Ekwadoru był uczony Pierre Bouguer (1698-1758), a w jej skład wchodził m. in. przyrodnik Charles Marie de La Condamine (1701-1774). Wyprawa spotkała się z nieufnością tubylców, niemogących uwierzyć, że przywiezione przez nią niezwykle kosztowne i skomplikowane instrumenty przeznaczone są do ściśle naukowych badań, a nie do jakichś całkiem innych celów, takich jak poszukiwanie złota. (Niektórych salonowiczów też nic nie przekona, że można robić coś wyłącznie dla nauki, a nie dla kasy – zupełnie jak tych tubylców...) 

W trakcie ekspedycji panowie uczeni mocno się ze sobą pokłócili i pomiary przeprowadzali oddzielnie. Przy okazji zajmowali się też badaniami przyrody (La Condamine był pierwszym Europejczykiem, który zgromadził informacje na temat kauczuku). Wyprawa przeciągała się, a jej członkowie oddzielnie docierali do Europy wybierając różne trasy. La Condamine przepłynął Amazonkę, a potem musiał czekać na neutralny statek, gdyż właśnie wybuchła wojna między Francją a Wielką Brytanią i statki francuskie były narażone na ataki korsarzy. Takie to były „przyjemności” prowadzenia badań naukowych w owych czasach... Do Europy dotarł w 1744 roku, w kilka miesięcy po Bouguerze, który wybrał prostszą drogę. Niektórzy członkowie ekspedycji wrócili jeszcze później.  

Ekspedycja do Laponii zaczęła się na wiosnę 1736 roku. Kierował nią Pierre de Maupertuis (1698-1759), wybitny naukowiec, któremu fizyka teoretyczna zawdzięcza jedną z podstawowych zasad: zasadę najmniejszego działania. W jej skład wchodził m. in. szwedzki uczony Anders Celsius (1701-1744), którego nikomu przedstawiać nie trzeba, bo to dzięki niemu odstępy między kreskami na termometrach są dzisiaj właśnie takie, jakie są. Wyprawa, zmagając się latem z chmarami insektów, a zimą z pięćdziesięciostopniowymi mrozami, dotarła aż za koło polarne i tam dokonała pomiarów. Maupertuis zorganizował prace w bardzo przemyślany sposób: podczas długich letnich dni prowadzono triangulację naziemną; wiosną i jesienią w ciągu niezbyt jeszcze zimnych nocy dokonywano obserwacji astronomicznych, mających na celu precyzyjne określenie współrzędnych geograficznych miejsc prowadzonych badań; natomiast zimą wykonywano obliczenia. Ekspedycja powróciła do Francji pod koniec lata 1737 roku. 

Wyniki pomiarów obu ekspedycji były jednoznaczne: jeden stopień łuku południka w pobliżu równika jest krótszy niż w okolicach podbiegunowych. Długość jednego stopnia południka wyznaczona w Ekwadorze wynosiła 110,6 kilometra, natomiast w Laponii ta wartość to 111,9 kilometra. (Mam nadzieję, że nie pomyliłem się w przeliczaniu ówczesnych jednostek francuskich na dzisiejsze kilometry...) Różnica jest na tyle duża, by można było przypisać ją błędom pomiarowym. Kształt Ziemi jest dokładnie taki, jaki przywidywał Newton. 

Myślicie, że w ten sposób spór się zakończył? Ale gdzie ta, ale gdzie ta... Zwolennicy Kartezjusza z Cassinim na czele oskarżyli członków wypraw o sfałszowanie wyników, a Maupertuisa zaczęto złośliwie nazywać „wielkim spłaszczaczem”. (To również typowe zachowanie. Jeśli jakiś rezultat nie zgadza się z czyimiś powziętymi wcześniej zapatrywaniami, natychmiast zostaje uznany za fałszerstwo albo przynajmniej za manipulację, a wyśmiewanie to typowa broń, gdy brakuje konkretnych argumentów. Czy nie jest tak z obecnymi zarzutami wobec wyników otrzymanych przez LHC, LIGO, wielkie teleskopy astronomiczne itp.?...) 

Co więcej, w kilka lat później kartezjaniści dostali potężne wsparcie od teoretyków. W 1748 roku francuska Królewska Akademia Nauk ogłosiła konkurs na pracę o ruchach Księżyca. Do konkursu zgłosiło się trzech najwybitniejszych podówczas matematyków: Leonhard Euler (1707-1783), Jean le Rond d’Alembert (1717-1783) i Alexis Clairaut (1713-1765). Wszyscy trzej doszli do tego samego wniosku: obserwowanych ruchów Księżyca nie da się wytłumaczyć za pomocą teorii Newtona! Euler w liście do Clairauta napisał: 

Mogę podać szereg dowodów na to, że siły, które działają na Księżyc, nie podlegają ściśle prawu grawitacji Newtona (…) Skłania mnie to do sądzenia, że przyczyną tych sił są wiry albo jakieś inne materialne czynniki, wtedy bowiem łatwo jest zrozumieć, że siły te powinny ulegać zmianie, kiedy są przenoszone przez jakiś inny wir. 

Czyżby Kartezjusz miał jednak rację?... 

Oczywiście, jak dzisiaj wiemy, nie miał. Wszyscy trzej wielcy uczeni popełnili podobne błędy. Problem ruchu Księżyca nie jest zagadnieniem dwóch ciał – Ziemi i naszego naturalnego satelity – ale trzech ciał, gdyż istotną rolę odgrywa także Słońce. Zagadnienie dwóch ciał rozwiązał już Newton, ale problem trzech ciał nie ma analitycznego rozwiązania: aby go ugryźć, trzeba stosować metody przybliżone. Obecnie świetnie wiemy, jak to robić, ale w połowie XVIII wieku mechanika ruchów ciał niebieskich dopiero się rodziła. Euler, d’Alembert i Clairaut zastosowali po prostu złe przybliżenia. Skoro ja mogłem się pomylić, to taki Euler też... (Wężykiem, Jasiu, wężykiem!) 

Pierwszym, który zdał sobie sprawę z błędu, był Clairaut. Poprawioną wersję swojej pracy opublikował pod tytułem „Teoria Księżyca, wydedukowana z jedynej zasady wzajemnego przyciągania z kwadratem odległości”, który miał podkreślać fakt, że autor korzystał wyłącznie z prawa grawitacji Newtona. 

Ostateczny cios koncepcji Kartezjusza zadała kometa Halleya. Halley w wydanym w 1705 roku dziele „Dyskusja astronomicznych komet” przeanalizował XVI- i XVII-wieczne obserwacje 24 komet za pomocą graficznej metody (opisanej w „Zasadach” Newtona) i odkrył, że orbity obiektów z lat 1531, 1607 i 1682 są bardzo podobne do siebie. Na tej podstawie wysnuł wniosek, że w ich przypadku mamy do czynienia nie z trzema różnymi, ale z jedną kometą obiegającą Słońce z okresem około 76 lat. W ten sposób przewidział, że kometa ta (dzisiaj nazwana jego imieniem) powróci w okolice Ziemi w 1758 roku. 

Bardziej szczegółowe obliczenia przeprowadził w 1757 roku Clairaut wraz ze współpracownikami. I faktycznie, pod koniec 1758 roku zaobserwowano kometę poruszającą się po orbicie wyznaczonej na podstawie prawa powszechnego ciążenia. Od tego momentu właściwie wszyscy poważni naukowcy akceptowali fizykę newtonowską, a teoria wirów Kartezjusza popadła w zapomnienie. 

Na zakończenie krótka uwaga. Z opisanej przeze mnie historii widać, jak bardzo krytykowana była teoria newtonowska. Przeciwko niej wytaczano argumenty zarówno teoretyczne, jak i eksperymentalne. Strzelano z najcięższych armat, a kanonierami byli najwybitniejsi uczeni epoki: Huygens, Leibniz, Bernoulli, Euler, d’Alembert i inni. Mimo to na koniec okazało się, że wszystkie strzały chybiły. Przy tak potężnej artylerii celującej w Newtona wszystkie obecne argumenty przeciwników Wielkiego Wybuchu, czarnych dziur, ciemnej materii itp. wyglądają jak pistoleciki na wodę.