Jaki kształt ma Ziemia i co z tego wynika?

Przed przeczytaniem tej notki proszę zapoznać się z wcześniejszymi z cyklu (Część 1, Część 2, Część 3).

W poprzednich notkach przyjmowałem, że Ziemia jest idealną kulą. Ale czy tak jest rzeczywiście? Problem kształtu naszego globu nabrał ogromnego znaczenia w 1. połowie XVIII wieku, a jego rozwiązanie przyczyniło się nie tylko do lepszego poznania samej Ziemi, ale także do rozstrzygnięcia jeszcze ważniejszej, a odległej na pozór kwestii. W owym czasie naczelnym tematem w nauce było pytanie, jaka siła jest odpowiedzialna za ruch planet wokół Słońca oraz księżyców wokół planet, i właśnie zbadanie kształtu Ziemi pomogło znaleźć na nie odpowiedź. Aby wyjaśnić, na czym polegał ten problem i dlaczego kształt naszej planety miał takie znaczenie dla jego rozwiązania, muszę najpierw opowiedzieć dość długą historię. 

Losy odkrywania prawa grawitacji zwykle przedstawia się w następujący sposób. Najpierw Kopernik stwierdził, że planety poruszają się wokół Słońca, następnie Kepler podał szczegółowe zasady tego ruchu, na ich podstawie Newton wydedukował prawo grawitacji, a kiedy to zrobił, od razu wszyscy byli szczęśliwi, przynajmniej do momentu, gdy pojawił się Einstein, który pokazał, że opis newtonowski jest przybliżeniem bardziej ogólnej teorii – co prawda znakomitym w przypadku niezbyt silnych pól grawitacyjnych, ale jednak tylko przybliżeniem. W rzeczywistości historia ta jest znacznie bardziej skomplikowana. 

Mikołaj Kopernik (1473-1543) w swoim dziele „O obrotach sfer niebieskich” zmienił ciało centralne Wszechświata z Ziemi na Słońce, ale nie rozważał szczegółowo przyczyny ruchu planet. Przyjmował za Arystotelesem i innymi uczonymi Starożytności, że są one doczepione do systemu kryształowych sfer, które obracają się bez tarcia, a w ruch wprawił je Pierwszy Poruszyciel (czyli Pan Bóg). Jednakże niedługo po śmierci kanonika z Fromborka, w 1577 roku duński astronom Tycho Brahe (1546-1601) stwierdził, że jest to niemożliwe. Z jego obserwacji jasnej komety wynikało bowiem, że porusza się ona pomiędzy planetami, czyli musiałaby przebijać się przez sfery – gdyby takowe faktycznie istniały. (Przed Tychonem sądzono, że komety nie są ciałami niebieskimi, ale zjawiskami zachodzącymi w ziemskiej atmosferze; dopiero Duńczyk odkrył ich kosmiczną naturę). 

Chyba pierwszym uczonym, który poważnie zastanawiał się nad przyczyną ruchu planet, był Johannes Kepler (1571-1630). Najbardziej znany jest ze swych trzech praw: pierwszego, które stwierdza, że planety poruszają się po elipsach; drugiego, opisującego zmiany prędkości planety na orbicie; i trzeciego, podającego matematyczny związek między odległością planety od Słońca a jej okresem obiegu (kwadrat okresu obiegu jest proporcjonalny do sześcianu odległości od Słońca). Prawa te są czysto kinematyczne, to znaczy nie mówią nic o siłach wywołujących ruch, a jedynie o jego własnościach. Kepler uczynił jednak także pierwszy krok w kierunku dynamiki Układu Słonecznego, starając się dociec, jakie siły zmuszają planety do krążenia. Słusznie uznał, że obiektem za to odpowiedzialnym jest Słońce, którego wpływ maleje wraz z odległością, niesłusznie zaś, że siła poruszająca planety to magnetyzm działający wyłącznie w płaszczyźnie równikowej Słońca. Chociaż akurat ta koncepcja Keplera była zasadniczo błędna, miała ogromne znaczenie dla dalszego rozwoju astronomii. Nauka ta wcześniej ograniczała się do opisu zjawisk obserwowanych na niebie, i dopiero Kepler przeniósł ją na wyższy poziom: od jego czasów zaczęto poszukiwać fizycznych przyczyn tych zjawisk. 

W następnych latach zaproponowano różne mechanizmy wyjaśniające orbitalny ruch planet. Dla przykładu, sugerowano, że popychać je może promieniowanie słoneczne. Największą popularność zdobyła jednak hipoteza wirów eteru, wysunięta przez René Descartesa (1596-1650), nazywanego w Polsce Kartezjuszem. 

Kartezjusz w swym wydanym w 1644 roku dziele „Zasady filozofii” przedstawił obraz Wszechświata, w którym wokół Słońca istnieje wir jakiejś subtelnej materii, a ciśnienie tego wiru popycha planety na orbitach. Z kolei planety mają swoje wiry, które pchają księżyce. Gwiazdy to odległe słońca, i też otoczone są przez wiry:

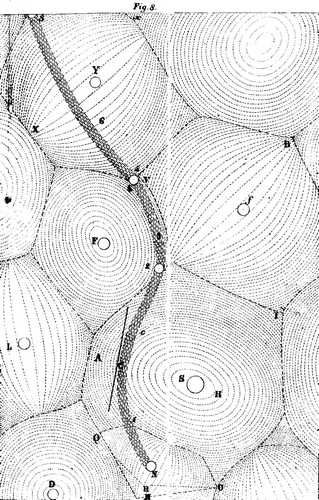
Ilustracja zamieszczona w „Zasadach filozofii” Kartezjusza

Oryginalna koncepcja wirów Kartezjusza miała charakter czysto jakościowy, ale stała się bardzo popularna, prawdopodobnie dlatego, że silnie przemawiała do wyobraźni. Łatwo było zwizualizować sobie obiekty, które przypominają wiry na wodzie, i sposób, w jaki poruszają one planety i księżyce.

Dla dalszego rozwoju nauki ogromne znaczenie miały inne osiągnięcia Kartezjusza. Stworzył geometrię analityczną, zajmował się optyką i fizjologią. Dla naszej historii ważny jest fakt, że jako pierwszy poprawnie (choć w dość skomplikowany sposób) sformułował zasadę bezwładności oraz zauważył, iż w przyrodzie musi istnieć coś, co dzisiaj nazywamy siłą odśrodkową (aczkolwiek nie podał opisującego ją wzoru). 

W 2. połowie XVII wieku koncepcja wirów Kartezjusza zdominowała fizykę (nazywaną wówczas filozofią naturalną). Byli jednak tacy, którzy poszli inną drogą – dziś wiemy, że słuszną, gdyż w końcu doprowadziła ona Newtona do sformułowania prawa grawitacji. Szczególną rolę odegrał tu Robert Hooke (1635-1703). To być może najbardziej niedoceniany uczony w historii. W szkołach uczymy się jedynie prawa Hooke’a, które podaje zależność odkształcenia jakiegoś materiału od przyłożonej siły, a jest to tylko jedno z wielu jego osiągnięć – i wcale nie najważniejsze. Tutaj opiszę tylko jego wkład w powstanie teorii grawitacji. 

W 1670 roku Hooke wygłosił w Londynie wykład, którego treść została opublikowana cztery lata później. Wysunął w nim trzy „przypuszczenia”. W pierwszym z nich stwierdza, że 

wszystkie bez wyjątku ciała niebieskie są obdarzone właściwością ciążenia, czyli przyciągania do swych środków, dzięki temu przyciągają (…) wszystkie inne ciała niebieskie. 

Jest to pierwsze sformułowanie prawa powszechnego ciążenia. Wynika z niego, że nie tylko Słońce ma wpływ na ruch planet (co już od dawna postulowano), ale i odwrotnie – planety wywierają wpływ na Słońce i na inne planety (co było absolutną nowością i stanowiło ogromny krok ku zrozumieniu grawitacji). 

Drugie przypuszczenie jest powtórzoną za Kartezjuszem zasadą bezwładności, ale w znacznie klarowniejszej formie: 

wszystkie ciała będące w ruchu jednostajnym po prostej pozostają w tym ruchu, dopóki nie zostaną przez jakieś działające moce odchylone i zmuszone do ruchu po okręgu, elipsie lub jakiej innej złożonej krzywej. 

Trzecie przypuszczenie mówi o zmniejszaniu się siły ciążenia wraz z odległością. Hooke nie potrafił jednak podać faktycznej postaci zależności, stwierdzając jedynie 

jakie są tego stopnie, tego jeszcze nie potwierdziłem doświadczalnie. 

Zależność tę znalazł Edmond Halley (1656-1742) – tak, ten od komety. Skorzystał on z wyniku otrzymanego przez holenderskiego uczonego Christiaana Huygensa (1629-1695). W 1673 roku Huygens opublikował pracę, w której podał wzór na wartość siły odśrodkowej. Halley zauważył, że jeśli siła odśrodkowa ma równoważyć przyciąganie Słońca, a jednocześnie ma być spełnione trzecie prawo Keplera (to o związku między okresem obiegu planety a jej odległością od Słońca), to siła przyciągania grawitacyjnego musi maleć wraz z kwadratem odległości. 

W ten sposób stworzono podstawy teorii grawitacji. Pozostawała jednak otwarta kwestia, czy teoria ta tłumaczy eliptyczny kształt planet. Tego ani Hooke, ani Halley nie potrafili wykazać. Udało się to dopiero Isaacowi Newtonowi (1643-1727), który musiał w tym celu wymyślić rachunek różniczkowy i całkowy. Wynik ten przedstawił w swych „Matematycznych zasadach filozofii naturalnej” – prawdopodobnie najważniejszym dziele w całej historii fizyki. Stało się ono podstawą całej mechaniki (i nie tylko). Newton rozwiązał problem, który dziś nazywamy zagadnieniem dwóch ciał, czyli ruchu dwóch obiektów pod wpływem wzajemnie wywieranej na siebie siły. Okazało się, że jeśli dwa ciała działają na siebie siłą, która maleje z kwadratem odległości, muszą poruszać się po jednej z krzywych stożkowych: hiperboli, paraboli lub elipsie. Tak więc eliptyczny kształt orbit planet znalazł teoretyczne uzasadnienie. Opisane w „Zasadach” metody pozwalały obliczać parametry orbit wszystkich ciał niebieskich – nie tylko planet, lecz także księżyców, komet i (w latach późniejszych) asteroid, gwiazd podwójnych, wielokrotnych itp. 

Wbrew temu, co się często sądzi, „Zasady” Newtona wcale nie zostały zaakceptowane z entuzjazmem przez cały ówczesny świat naukowy. Dla wielu założenie, że wszystkie masy wzajemnie się przyciągają, było czysto arbitralne i nieudowodnione, a obraz świata zaproponowany przez Newtona nie miał nic wspólnego z rzeczywistością. W owym czasie nawet niektórzy najwybitniejsi uczeni nie byli w stanie zrozumieć istoty teorii Newtona. Sytuacja jako żywo przypominała dzisiejszą krytykę co bardziej abstrakcyjnych hipotez dotyczących struktury mikroświata. (Więcej na ten temat napisałem w notce „Newton w stringach, czyli o krytykowaniu nowatorskich idei w nauce”). 

Jednym z głównych zarzutów stawianych teorii powszechnego ciążenia było wprowadzenie w niej „siły działającej na odległość”. Sam Newton, pytany o jej pochodzenie, napisał słynne słowa: „hypotheses non fingo” (hipotez nie wymyślam). Dla wielu współczesnych koncepcja wirów Kartezjusza nadal była bardziej atrakcyjna, gdyż ich działanie łatwiej można sobie wyobrazić niż tajemniczą siłę operującą na ogromnych odległościach. 

Wydawać by się mogło, że teoria Newtona miała znaczącą przewagę nad koncepcją Kartezjusza, gdyż miała charakter ilościowy, podczas gdy ta druga – czysto jakościowy. Jednakże na początku XVIII wieku to się zmieniło: podjęto próby zmatematyzowania również teorii wirów. W 1707 roku Phillippe Villemot pokazał, że przy pewnych założeniach dotyczących wirów można uzyskać znaleziony przez Keplera związek między okresem obiegu planety a jej odległością od Słońca. W 1730 roku jeden z przedstawicieli wspaniałego szwajcarskiego klanu Bernoullich, Johann (1667-1748), pokazał z kolei, że – znowu przy pewnych założeniach – także eliptyczny kształt orbit nie jest sprzeczny z hipotezą Kartezjusza. 

Mieliśmy więc dwie teorie, przynajmniej na pozór równoprawne. Jak stwierdzić, kto ma rację: Kartezjusz czy Newton?... 

I tu, po tym długaśnym wprowadzeniu, wreszcie dochodzimy do sprawy kształtu Ziemi. Obie konkurencyjne teorie przewidywały, że nasza planeta nie może być idealną kulą. Newton w „Zasadach” pokazał, że z powodu swego wirowania Ziemia musi być spłaszczona przy biegunach, natomiast zwolennicy Kartezjusza na podstawie rozważań jakościowych wysnuli wniosek, że ciśnienie wiru powinno spowodować, iż jest ona wydłużona niczym jajko. A zatem, wyznaczenie precyzyjnego kształtu Ziemi powinno pomóc w rozstrzygnięciu sporu. 

Aby to uczynić, należało zmierzyć długość jakiegoś fragmentu południka – na przykład jednego stopnia – w różnych szerokościach geograficznych. Dla idealnej kuli ta długość jest w każdym jej miejscu jednakowa:

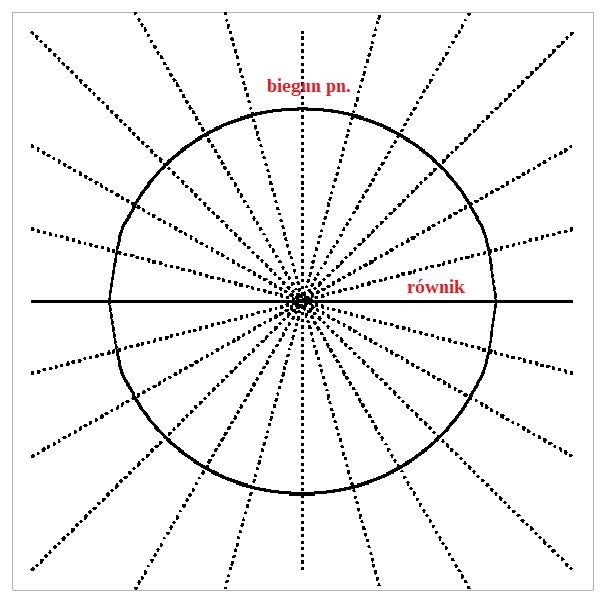
ale dla obiektu spłaszczonego przy biegunach jest ona większa bliżej równika, zaś mniejsza w dużych szerokościach geograficznych:

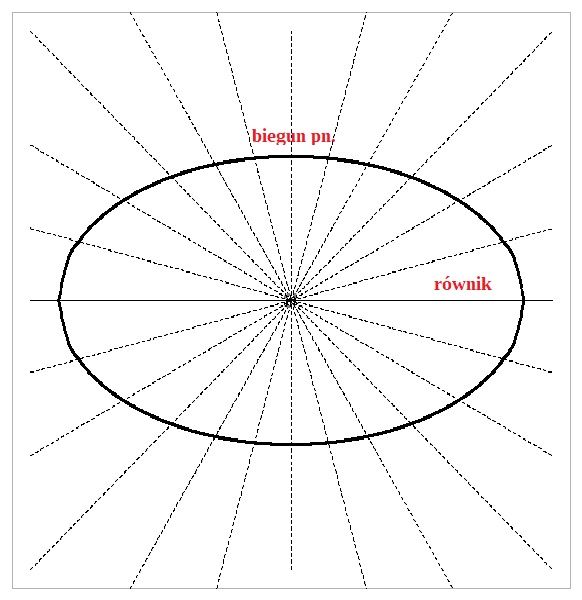
zaś dla obiektu wydłużonego odwrotnie – długość łuku jednego stopnia jest większa blisko bieguna niż w małych szerokościach geograficznych:

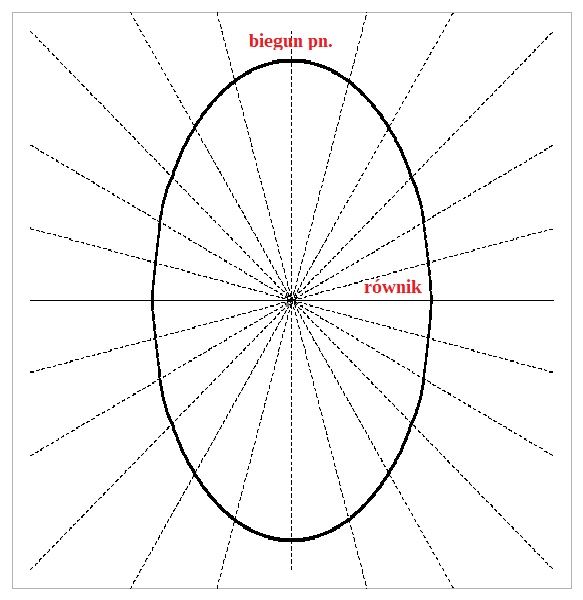
Na początku XVIII wieku, kiedy dyskusja między kartezjanistami a newtonowcami osiągnęła apogeum, kwestię kształtu Ziemi postanowili rozstrzygnąć uczeni francuscy. Tak się złożyło, że już wcześniej, bo w latach 1669-70, pracownik paryskiego Obserwatorium Astronomicznego, jezuita Jean-Félix Picard (1620-1682) zmierzył długość jednego stopnia łuku południka na odcinku od Paryża w kierunku południowym do miejscowości Sourdon. W pomiarach korzystał z opisanej w poprzedniej notce metody triangulacyjnej. Picard był świetnym astronomem praktykiem; jednym z jego osiągnięć było ulepszenie tzw. mikrometru pozycyjnego, czyli systemu nitek umieszczonych w polu widzenia okularu teleskopu, służących do precyzyjnego określania odległości kątowych. Ponieważ w urządzeniach pomiarowych używał lunetek, wyznaczona przez niego długość jednego stopnia południka – 110,46 kilometra – jest znacznie dokładniejsza niż wynik Snelliusa otrzymany ponad pół wieku wcześniej (błąd pomiaru Picarda jest mniejszy niż pół procenta).

W 1712 roku dyrektorem Obserwatorium Paryskiego został Jacques Cassini (1677–1756). Zastąpił na tym stanowisku swego ojca, Giovanni Domenico Cassiniego (1625–1712), znanego z odkrycia księżyców Saturna i przerw w jego pierścieniach, którego imieniem nazwano sondę wysłaną do tej planety. Jacques Cassini postanowił zmierzyć długość łuku południka na północ od Paryża w celu porównania jej z wartością Picarda. W 1713 roku dokonał pomiarów na trasie z Dunkierki do Perpignan, a wyniki opublikował siedem lat później. Z dwóch analiz wyszły mu wyniki odpowiednio 111,282 i 111,211 kilometra dla jednego stopnia szerokości geograficznej – czyli więcej niż wynik Picarda uzyskany w pomiarach prowadzonych bardziej na południe. Wyglądało na to, że długość jednego stopnia łuku wzrasta w stronę bieguna, a więc Ziemia ma kształt wydłużony. 

Czyżby Kartezjusz miał rację?… 

Dalszy ciąg nastąpi.

Apdejt. Do notki tej, niestety, wkradły się błędy, które skorygowałem w następnej części.