Przed przeczytaniem tej notki proszę zapoznać się z Częścią 1 i Częścią 2.
Przełom XV i XVI wieku to początek epoki wypraw dalekomorskich. Po oceanach świata zaczęło pływać coraz więcej statków i okrętów, najpierw hiszpańskich i portugalskich, ale niedługo dołączyły do nich także floty angielska, francuska i holenderska. Dobra znajomość rozmiarów Ziemi stała się koniecznością, należało więc przeprowadzić badania pozwalające wyznaczyć obwód południka znacznie dokładniej. Zadania tego podjął się żyjący w Holandii fizyk i matematyk Willebrord Snell (1580-1626), używający zlatynizowanej wersji swego nazwiska – Snellius. Uczony ten znany jest głównie z odkrycia matematycznego prawa załamania światła i sformułowania twierdzenia sinusów, którymi od wielu lat nauczyciele katują uczniów szkół średnich; wniósł on jednak także ogromny wkład w wyznaczenie rozmiaru naszej planety.
Snelliusa zainspirowała oryginalna praca Eratostenesa. Postanowił powtórzyć pomiary greckiego astronoma, ale o wiele bardziej precyzyjnie. W tym celu jako jeden z pierwszych zastosował w praktyce metodę triangulacji.
Wspomniałem już wcześniej, że największą trudność w dokładnym wyznaczeniu obwodu Ziemi stanowi precyzyjny pomiar odległości między dwoma dalekimi miejscami. W 1533 roku inny holenderski uczony, kartograf Gemma Frisius (1508-1555) zaprezentował pomysł, jak do tego celu można wykorzystać geometryczne własności trójkątów. Ze szkoły wiemy, że znając długość jednego boku i wartości dwóch kątów trójkąta można określić wszystkie jego parametry: pozostałe dwa boki, trzeci kąt, wszystkie wysokości itp. Zgodnie z koncepcją Frisiusa, aby zmierzyć dużą odległość, wystarczy precyzyjnie wyznaczyć tylko jedną, niezbyt wielką długość pewnego odcinka, a dalsza część pracy polega wyłącznie na pomiarze kątów. Wyjaśnia to poniższy rysunek.
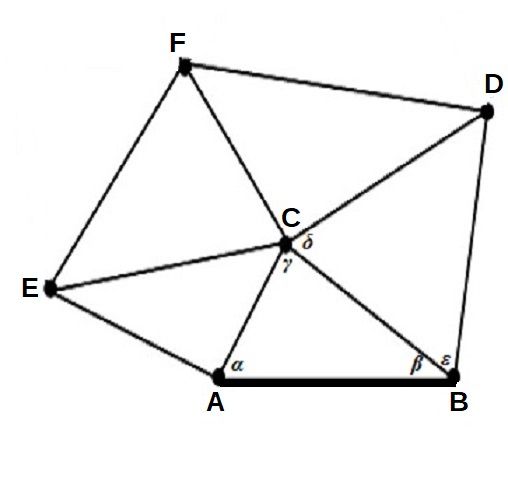
Wybieramy dwa punkty A oraz B i z największą możliwą dokładnością wyznaczamy dzielącą je odległość. Odcinek AB stanowić będzie tak zwaną bazę triangulacyjną. Wybieramy teraz punkt C i z punktu A mierzymy kąt α między bazą triangulacyjną a kierunkiem na punkt C, a następnie z punktu B mierzymy kąt β, również między odcinkiem AB a kierunkiem na punkt C. Znając długość jednego boku i wartości dwóch kątów trójkąta można określić inne jego parametry, w tym długość boku BC.
Skoro już ją znamy, to teraz możemy jej użyć jako bazy do dalszych pomiarów. Wybieramy punkt D, mierzymy kąty δ i ε i powtarzamy całą procedurę. Analogicznie robimy z trójkątem ACE (tutaj bazą dla nas będzie bok AC). W ten sposób za pomocą kolejnych takich kroków jesteśmy w stanie pokryć pomiarami cały interesujący nas obszar.
Tę właśnie metodę wymyślił Frisius. Zaletą triangulacji jest brak konieczności bezpośredniego dokładnego mierzenia dużych odległości, co jest niezmiernie uciążliwe. Wystarczy zmierzyć jeden niezbyt długi odcinek. Cała reszta pracy polega na wielokrotnym, ale o wiele łatwiejszym pomiarze kolejnych kątów. Urządzenia do precyzyjnego wyznaczania kątów na Ziemi znano już w XV wieku. Przypominały one dzisiejsze teodolity, choć oczywiście pozbawione były lunety, którą wynaleziono dopiero w XVII wieku. (Samo słowo teodolit pojawiło się po raz pierwszy w książce XVI-wiecznego matematyka angielskiego Leonarda Diggesa; co ciekawe, nikt nie wie, jaka jest etymologia tej nazwy. Teodolit Diggesa można zobaczyć TUTAJ.)
Jeżeli badany obszar jest znaczny, w obliczeniach trzeba uwzględniać kulistość Ziemi. Zamiast trójkątów na płaszczyźnie należy rozważać trójkąty sferyczne, czyli trójkąty leżące na powierzchni kuli:
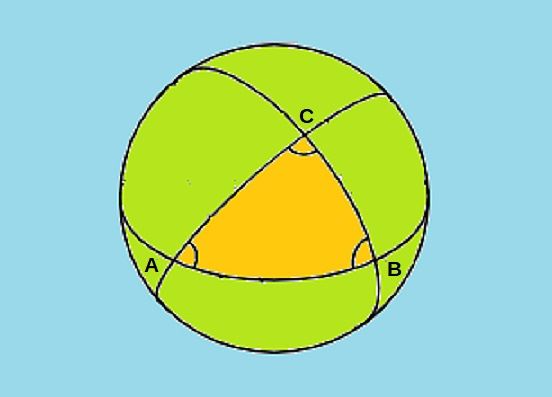
Oczywiście, pokazany na rysunku trójkąt sferyczny ABC jest znacznie większy od tych, jakie używa się w triangulacji. Trójkąty sferyczne mają nieco inne własności niż trójkąty płaskie. Dla przykładu, suma ich kątów jest większa od 180º. Mogą być trójkąty sferyczne z dwoma, a nawet z trzema kątami prostymi. Dla triangulacji nie jest to żaden problem, bowiem zasady trygonometrii sferycznej (czyli działu matematyki zajmującego się takimi obiektami) znali już starożytni.
Triangulacja do niedawna była jednym z najdokładniejszych sposobów określania odległości na Ziemi. Aby wyraźnie zaznaczyć wierzchołki trójkątów, specjalnie stawiano wysokie wieże triangulacyjne. Stały się one powszechnym składnikiem pozamiejskiego krajobrazu. Sam jako młody chłopak w czasie wakacji właziłem na takie trianguły, żeby z góry podziwiać okoliczną panoramę.
Wieża triangulacyjna na Baraniej Górze (fot. Pudelek, wiki, GNU Free Documentation License)
W 1615 roku metodę triangulacji wykorzystał Snellius do wyznaczenia odległości między dwoma miastami holenderskimi: Bergen op Zoom i Alkmaarem. Leżą one prawie na tym samym południku, a różnica szerokości geograficznych jest nieco większa niż 1º. W pracy pomagali mu dwaj uczniowie, austriaccy baronowie Sterrenberg. W owym czasie nie wybudowano jeszcze wież triangulacyjnych, ale Holandia już wtedy była gęsto zasiedlona, dlatego badacze jako punkty pomiarowe mogli wykorzystać niezbyt oddalone od siebie wieże kościołów. Do wyznaczania kątów używali tego oto kwadrantu:
Kwadrant Snelliusa, Museum Boerhaave, Lejda (fot. prof. Jos van den Broek, wiki, Creative Commons Licence)
W ten sposób Snellius zmierzył odległość między Bergen op Zoom i Alkmaarem. Znając różnicę szerokości geograficznych tych miast (którą można wyznaczyć metodą opisaną w Części 2 tego cyklu), nie ma już problemu z obliczeniem obwodu południka. W 1617 roku Snellius opublikował swoje wyniki w książce pod znamiennym tytułem „Eratosthenes batavus, de terrae ambitus vera quantitate”, który można chyba przetłumaczyć jako „Eratostenes holenderski, zakres prawdziwej wielkości Ziemi”. Jeśli przeliczymy używaną wówczas miarę długości na jednostki współczesne, okaże się, że wyliczony przez Snelliusa obwód Ziemi to 38 653 kilometry (co odpowiada promieniowi 6152 kilometrów), czyli zaledwie 3,4 procenta mniej od prawdziwej wartości.
Ciąg dalszy nastąpi...
