Choć atmosfera nie sprzyja dochodzeniu do porozumienia, pocieszać się można tym, że w ogóle zapowiada się dyskusja nad konstytucją. Solidnie zażenowany awanturą trybunalską, rezerwuję swoją pasję dla sprawy ordynacji. Dziś zapowiedziany model probabilistyczny systemu d'Hondta.
Rzecz przedstawiałem w poprzedni wtorek na sympozjum organizowanym przez Centrum Badań Ilościowych nad Polityką UJ (link na końcu). Od strony praktycznej jest to wyjaśnienie, w jaki sposób można przeliczyć wyniki ogólnokrajowych sondaży na spodziewany podział mandatów bez żmudnego a wątpliwego szacowania podziału głosów pomiędzy okręgi. To pokazanie kuchni notki z wieczoru wyborczego. Szerszy ogląd to pytanie o sens konstytucyjnego wymogu proporcjonalności. Tytułem zniechęcenia dla miłośników politycznych ustawek uprzedzę, że będzie trochę matematyki, nawet jeśli na poziomie szkoły podstawowej. Dociekliwych to nie powinno zniechęcać. Moja córka, gdy miała sześć lat, powiedziała kiedyś do siebie - "to trudne, ale nie za trudne dla takiej małej, zdolnej dziewczynki".
Na początek wyjaśnienie, jak dokładnie działa mechanizm stosowany w Polsce do podziału mandatów w okręgu. Powszechnie znana jest jego formuła ilorazowa (podziel głosy oddane na listy przez kolejne liczby całkowite, etc.). Taka formuła gmatwa niemożebnie całkiem prostą sprawę. W innej formule metoda sprowadza się bowiem do jednego zdania. Musimy znaleźć taką liczbę, że gdy podzielimy przez nią głosy zdobyte przez wszystkie listy i zaokrąglimy w dół, to rozdzielimy tyle mandatów, ile przysługuje danemu okręgowi. Uświadomienie sobie tego zawdzięczam dr Jackowi Hamanowi z UW, który rzecz opisał w swojej książce "Demokracja, decyzje, wybory".
Ten w sumie prosty mechanizm ma ciekawe konsekwencje. Ich zrozumienie wypada zacząć od wyjaśnienia, jak szukać należy kluczowej dla metody liczby, przez którą będziemy dzielić głosy. Pierwszym krokiem jest wyliczenie "kwoty prostej", czyli głosów odpowiadających w okręgu jednemu mandatowi. Dzielimy sumę głosów oddanych na wszystkie partie biorące udział w podziale mandatów przez liczbę mandatów w okręgu i już. Teoretycznie jest możliwe, że teraz wystarczy pójść w drugą stronę, by rozwiązać całe zadanie. Jeśli podzielimy wyniki każdej z partii przez taką kwotę, to rozdzielimy wszystkie mandaty. Stanie się tak jednak tylko wtedy, gdy każda partia dostanie idealnie wielokrotność takiej kwoty. Jest to skrajnie nieprawdopodobne. W praktyce przydzielonych tą metodą mandatów pełnych jest mniej niż mamy ich wszystkich rozdzielić. Każdej partii zostaje bowiem jakiś ułamek - naddatek na kolejny mandat. Naddatek ten obcinany jest przy okazji zaokrąglenia. Suma takich ułamkowych naddatków odpowiada liczbie mandatów, które nam zostały do rozdzielenia. Jedno jest tylko pewne - żadna partia nie dostanie mandatów mniej, niż ma mandatów pełnych, wyliczonych dzięki podzieleniu jej wyniku przez kwotę prostą.
Jeśli mamy rozdzielić pozostające ciągle w puli mandaty, musimy zmniejszyć kwotę, przez którą będziemy dzielić głosy. Każde zmniejszenie kwoty powoduje wzrost naddatków partii. W którymś momencie naddatek którejś z partii urośnie na tyle, że zrówna się z naszą nową kwotą. Przeskalowanie kwoty musimy robić aż do momentu, gdy rozdzielimy wszystkie mandaty.
Najlepiej zobaczyć jak to działa na przykładzie. Na podwójnym wykresie, w każdym z naszych okręgów, pokazano drogę ku mandatom dwóch partii - PiS i Nowoczesnej. Na szaro zaznaczono mandaty pełne. Ujemną wartość przypisano naddatkom, wyrażonym jako ułamek mandatu. Wreszcie na zielono pokazano mandaty zdobyte na skutek przeskalowania - czyli różnicę pomiędzy ostateczne zdobytymi mandatami a mandatami pełnymi.
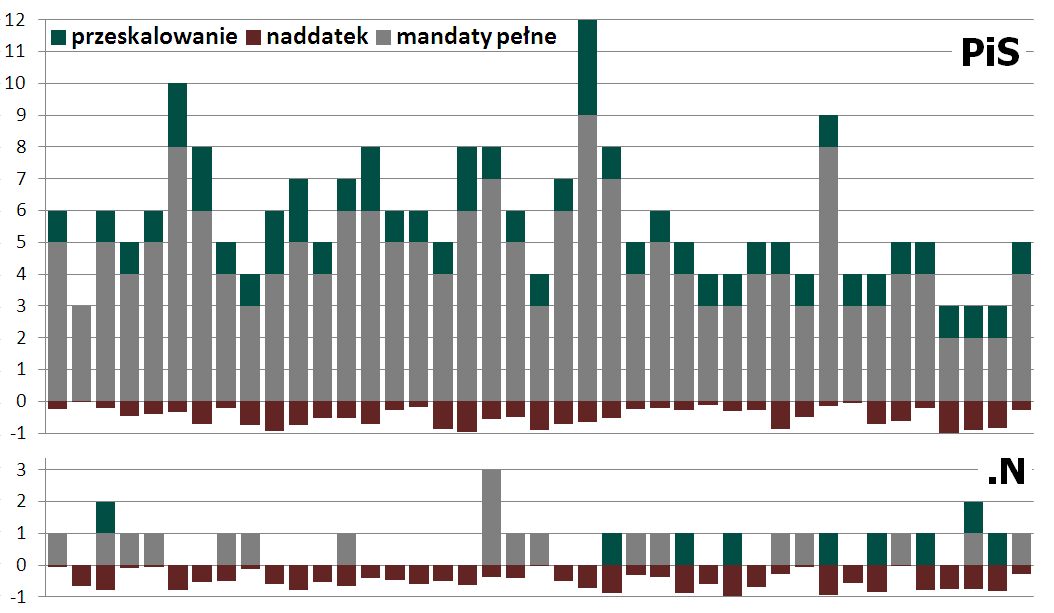Widać tu kluczową dla sprawy różnicę pomiędzy partią dużą i małą. To, że partia duża ma więcej mandatów pełnych jest oczywiste. Znacznie ważniejsze jest to, że partia największa ma średnio takie same naddatki jak partia o kilkukrotnie niższym poparciu. To wynika z rachunku prawdopodobieństwa - wartość oczekiwana takiego naddatku to pół mandatu. Pomimo podobnych naddatków, liczba mandatów otrzymywanych przez partie w wyniku przeskalowania jakościowo się różni. PiS dostał ich 48 zaś Nowoczesna tylko 9. Dlaczego - to właśnie kluczowy efekt systemu.
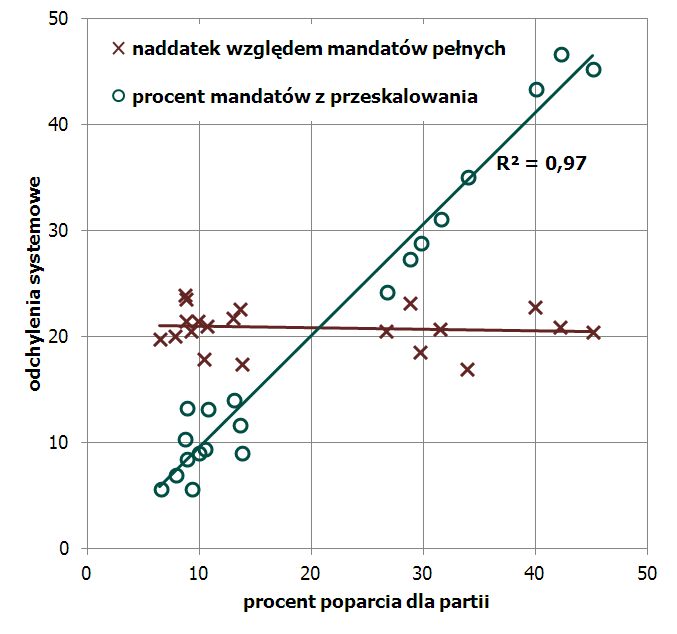
Jeśli zmniejszamy kwotę, prawdopodobieństwo zdobycia mandatu jest zależne od wielkości partii. Wydawać by się mogło, że decyduje o tym naddatek na kolejny mandat. Jest jednak czynnik ważniejszy. Im więcej ktoś już ma mandatów pełnych, tym więcej zyskuje na zmniejszeniu kwoty - każdy pełny mandat generuje mu dodatkowy naddatek na kolejny mandat. Gdy okręgów jest 41, prawo wielkich liczb może jeszcze nie działa, lecz prawdopodobieństwo nadzwyczajnego odchylenia od wartości oczekiwanej jest niewielkie. Widać to na wykresie, na którym pokazano oba efekty dla wszystkich czterech wyborów prowadzonych w obecnym systemie i wszystkich 20 ogólnopolskich komitetów, które załapały się w nich na mandat. Na osi poziomej efektywne poparcie dla partii (czyli po odliczeniu ugrupowań podprogowych). Krzyżykami pokazano sumę naddatków we wszystkich okręgach wyrażoną w mandatach. Kółkami - jaki procent mandatów przyznawanych dzięki przeskalowaniu kwoty zdobyła dana partia.
O ostatecznym podziale mandatów przesądzają zatem dwa kroki. Najpierw wszystkie partie wrzucają do wspólnego kociołka po 20,5 mandatu (w polskich realiach, czyli przy 41 okręgach). Ten "wsad do kotła" nie zależy od wielkości poparcia dla partii, jeśli ma ona więcej niż 5% głosów. Jednak z tak stworzonego wspólnego kociołka więksi wyjadają więcej. Tu rodzi się ich nagroda i strata mniejszych. Całość wyraża się wzorem:
S = V∙M – D/2 + V∙D∙P/2
S – liczba mandatów
M – liczba mandatów w parlamencie
V – udział partii w efektywnie oddanych głosach
D – liczba okręgów wyborczych
P – liczba partii biorących udział w podziale mandatów
Im więcej partii bierze udział w podziale mandatów, tym większy jest kociołek i tym więcej zyskują na mechanizmie ci, którzy są więksi od średniej. Jednocześnie każdy z mniejszych traci wtedy mniej. Wykres spodziewanego udziału w mandatach, w zależności od wielkości partii i liczby partii nad progiem, wygląda tak:
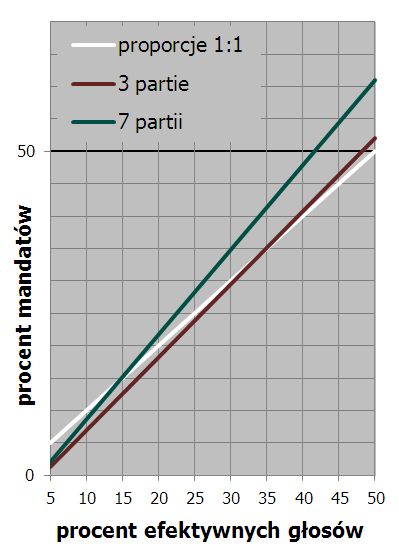
W czterech wyborach przeprowadzanych w tym systemie liczba partii wynosiła: raz 4, raz 6 i dwa razy po 5. Pokazane linie dla 3 i 7 partii są więc brzegami nieco poszerzonego wachlarza. Generalnie system jest proporcjonalny i to nawet liniowo, tyle, że nie jest to proporcja 1:1. Żeby była jasność - nie jestem wcale wrogiem takiego mechanizmu. Wręcz przeciwnie. Uważam, że większym partiom należy się premia za utrzymanie jedności. Ta, którą tworzy nasza liczba okręgów, jest bardzo rozsądna. Są tu jednak cztery "ale".
Po pierwsze nie wiem, jak z takim zjawiskiem mogą sobie radzić konstytucjonaliści. Co prawda w rachunek prawdopodobieństwa można po prostu nie wierzyć, lecz bardzo mnie ciekawi, co by powiedzieli na wpisanie takiego wzoru do procedury podziału mandatów w skali kraju.
Po drugie - to jest tylko wartość oczekiwana, zaś konkretne przypadki mogą się tu nieco różnić. Na przykład Kukizowi się poszczęściło i dostał o 3 mandaty więcej, niż można się tego było spodziewać - liczby otrzymanych przez niego głosów wpasowały się lepiej w ostateczne kwoty. Nie jest wcale wykluczone, że któregoś dnia takie odchylenia przesądzą o tym, kto stworzy rząd.
Po trzecie - podział na okręgi ze sztywną liczbą mandatów prowadzi do innych jeszcze systemowych odchyleń siły partii. Partie z wyższym poparciem w okręgach o wyższej frekwencji tracą, zaś zyskują te, które mają lepszy wynik w okręgach o niższej frekwencji. System przesuwał równowagę pomiędzy PiS i PO o średnio 6 mandatów na niekorzyść tej ostatniej partii. Jak dotąd nie przesądziło to nigdy o ostatecznym składzie rządu, lecz gdyby tak się stało, trudno byłoby dla tego stanu znaleźć przekonujące usprawiedliwienie.
Po czwarte (dla mnie najważniejsze) - okręgi wielomandatowe mają tragiczne skutki na polu napięć terytorialnych oraz dla relacji wewnątrz partii. Ten sam efekt można jednak uzyskać bez nich, tylko trzeba powiedzieć otwarcie, że się tego chce, nie zaś udawać, że tak to tylko wyszło mimochodem.
Tak, czy inaczej, zrozumienie jak to działa jest dla mnie bardzo ważne, nie tylko dlatego, że oszczędza czasu przy obliczaniu spodziewanej liczby mandatów. To uczytelnienie przekazu wysyłanego przez system do klasy politycznej: jeśli zamierzacie się podzielić i wystartować jako dwie partie, to d'Hondt be surprised - dostaniecie mniej mandatów, niż moglibyście zdobyć wtedy, gdybyście startowali razem.
PS. Nieocenioną pomocą w zrozumieniu tego mechanizmu byli dla mnie cierpliwi rozmówcy - profesorowie: Wojciech Słomczyński, Karol Życzkowski, Jacek Haman i Bartłomiej Michalak. Wielkie dzięki!
PS2. Puchar Pytii
Inne tematy w dziale Polityka
