59. Ostatnie dwie minuty. Rekonstrukcja trajektorii prezydenckiego tupolewa.

Końcowe zniżanie TU-154M z wysokości kręgu do lądowania na pasie 26 lotniska Siewiernyj w Smoleńsku dnia 10.04.10 trwało dwie minuty. Trajektoria nie była właściwa. Działo się wiele niepokojących rzeczy. Lecz skąd w ogóle wiemy, jaka dokładnie była? Nie została przecież zapisana bezpośrednio i w całości, w czarnych skrzynkach. Musi być jakoś odtworzona z parametrów lotu zapisanych w pamięci rejestratorów. Gdy badamy końcowe 4.6 s lotu po urwaniu skrzydła na brzozie lekarza Bodina, to pomagają nam świadkowie -- i ludzie i najważniejsi, niemi świadkowie - dziesiątki uszkodzonych drzew. Ale etap lotu, gdzie załoga podejmowała ostatnie świadome decyzje, miała jeszcze różne opcje, ukryty był prawie cały w chmurze.

W tej czysto technicznej notce rozważymy metody rekonstrukcji trajektorii podejścia przed utratą części skrzydła. Użyję trzech metod opartych na dynamice i aerodynamice. Najlepszą zgodność z danymi o położeniu samolotu w funkcji czasu:  alarmami TAWS/GPS, wysokościami wypowiadanymi w kokpicie, i w końcu z wysokościami uderzeń w drzewa, daje metoda, w której  rozwiązujemy złożone równanie algebraiczne do wyznaczenia kątów natarcia i nachylenia trajektorii w każdej chwili, korzystając z danych z rejestratorów. Dokładność rekonstrukcji jest wysoka, ok. dwóch metrów w okolicy brzozy, a kilkunastu metrów aż do odległości 11.28 km od pasa. Trajektoria prowadzi do zderzenia z brzozą, dokładnie odpowiadając prawdziwemu przebiegowi katastrofy; zgadza się czas zdarzenia, wysokość samolotu i chwilowa prędkość wznoszenia.

WSTĘP

Pierwszą całościową prezentację, zarówno danych z czarnych skrzynek jak i wynikowej historii zniżania i trajektorii lotu, zaprezentował rosyjski komitet badania wypadkow lotniczych MAK.   W r. 2011 umieścił trajektorię pionową na rys. 45-46 swego raportu końcowego.

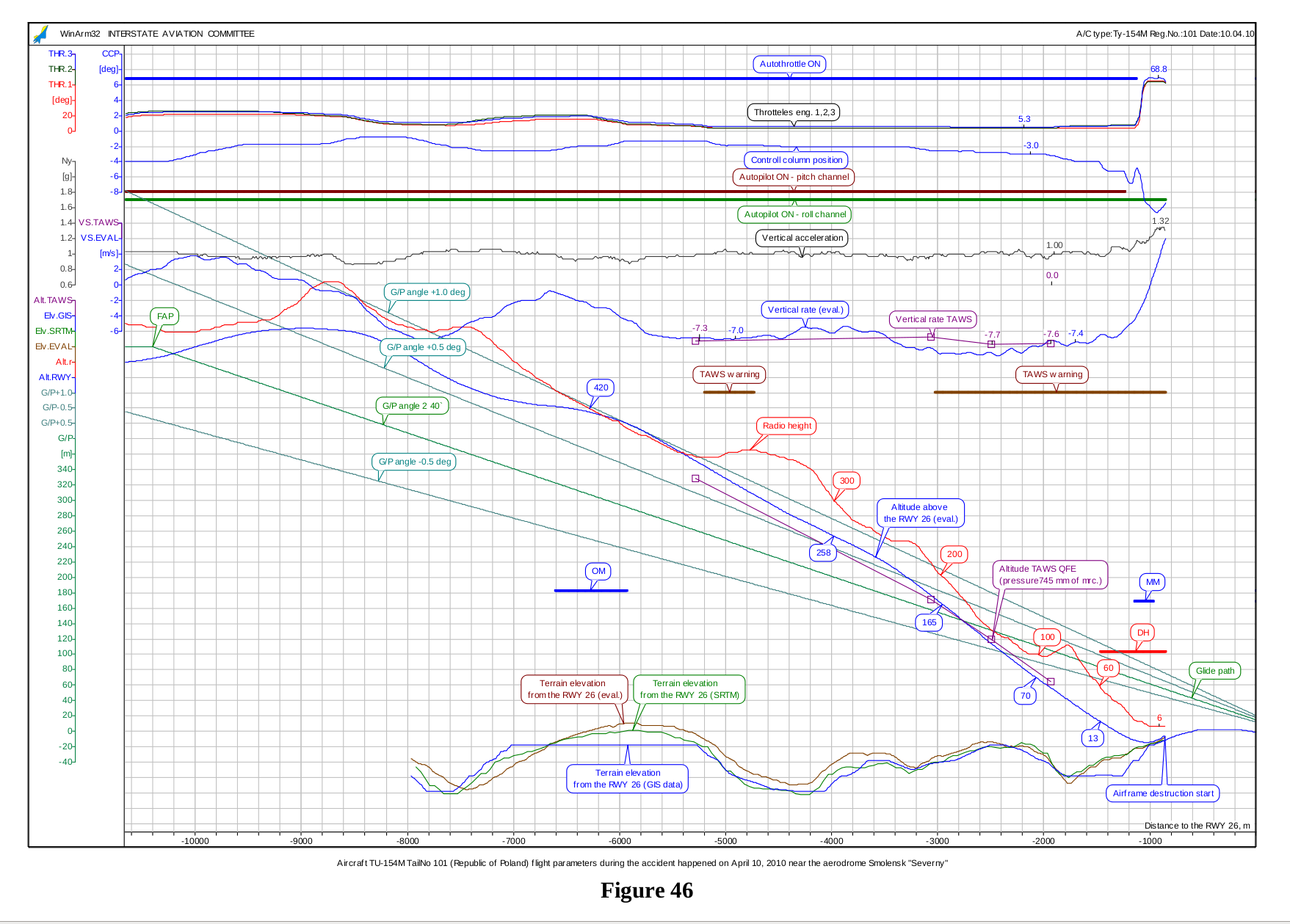
Rys.1. Trajektoria pionowa komitetu MAK. (http://planets.utsc.utoronto.ca/~pawel/pix/fig-mak-46.png).

Również polska komisja badania wypadków lotn. w lotnictwie państwowym, KBWLLP,  opublikowała swoją trajektorię:

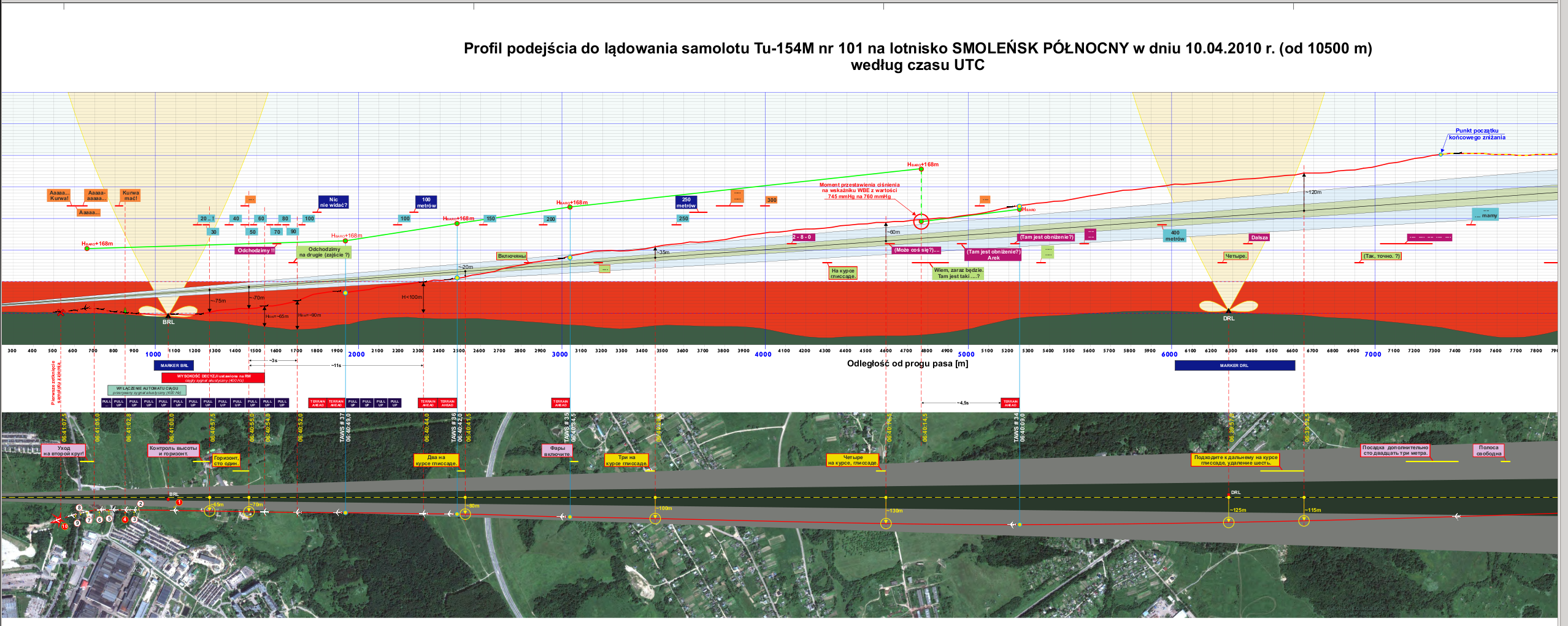
Rys.2. Trajektoria komisji KBWLLP. (http://planets.utsc.utoronto.ca/~pawel/pix/fig-KBWLLP-1.png)

Jednak żadna z komisji badania wypadków nie opisała swej metody. Widać, że nie uzyskano tych samych kształtów trajektorii. Trajektoria MAK jest gładsza i (zgodnie z opisem rysunku) obliczona. Najpewniej korzysta w jakiś sposób z całkowania prędkości pionowej Vz, jednak w jaki sposób wyznaczono Vz(t) nie wyjaśniono. Z kolei oficjalna trajektoria polska zmienia nachylenie do horyzontu w górę i w dół. To typowe dla metody opisanej poniżej jako nr. 1. Zapewnie nie należy przywiązywać zbytniej wagi do drobnych zagięć tej trajektorii.

Badał trajektorię Zespół Biegłych (ZB) prokuratury wojskowej WPO. Zespół nota bene później bez dużych zmian osobowych przeszedł za rządów PiS do prokuratury krajowej i nadal istnieje, choć w omawianej tematyce już nie działa. ZB przekazał opinie końcowe w zakresie badań technicznych i odsłuchowych, był pytany o poprawki i dostarczył je (wspominam o tym, gdyż opinia publiczna przestała być informowana o postępach po tzw, dobrej zmianie i może nie wiedzieć, że poprawki do Opinii Kompleksowej ZB istnieją. Proszę zwrócić się o informację do prokuratora Pasionka i min. Ziobry, może odpowiedzą :-| Tak czy owak, nie mogę tu pokazać trajektorii ZB. Niektórzy twierdzą, że istnieje i nie różni się wiele od pokazanych poniżej.

Do analizy przystąpili zaraz po katastrofie badacze niezależni. Z teodolitem wybrali się do Smoleńska i dostali zgodę właściciela działki lekarza N. Bodina na pewne pomiary już w maju 2010 r. autorzy serii książek Ostatni Lot (ostatnia podsumowująca książka z r. 2018  https://ksiegarnia.proszynski.pl/product,72708). Mierzyli ukształtowanie terenu pod drogą podejścia. Uzyskane wyniki przekazali mi wcześnie, stąd od dawna wiedziałem o paru-metrowej rozbieżności między wysokościami terenu wzgl. pasa w ich pomiarach, w raportach MAK i KBWLLP (każdy z nich miał nieco inny profil terenu). W sumie jest to nieuniknione, że są te rozbieżności wielu metrów wysokości. Wszyscy łącznie z Google Map posługują się danymi obarczonymi co najmniej taką niepewnością w pionie, typową dla systemu GPS bez specjalnego wspomagania. Nie warto mieć ambicji poprawiać tę dokładność, jeśli chodzi o ścieżkę podejścia PLF 101, warto natomiast mieć gęstą siatkę wartości na mapie, na linii podejścia. 

METODY WYZNACZANIA TRAJEKTORII PIONOWEJ 

Ponieważ nie zajmujemy się tu w zasadzie trajektorią na mapie, tj. zmiennym nieco kierunkiem lotu PLF 101 na ostatniej prostej, możemy sprowadzić nasze zadanie do znalezienia funkcji z(x) lub jeszcze lepiej z(t) i x(t), tj. historię czasową ruchu po "wyprostowanej" trajektorii.

1.   Altymetria radarowa i kartografia terenu pod samolotem

W tej metodzie pokazaną np. na rys. 46 MAK-u RA (radio altitude; zwana też RW lub wysokością radiową) znaną z FDR (Flight Data Recorder MSRP64, dane powielone w polskim ATM-QAR) dodajemy do wysokości nad progiem pasa 26 na lotnisku Siewiernyj, H(x), uzyskując szukaną trajektorię pionową względem pasa startowego

z(x) = RA(t(x)) + H(x).

Jak widać, RA(t) w FDR  oraz H(x) na mapie są funkcjami innych zmiennych, dlatego musimy być w posiadaniu odpowiedniej funkcji do przeliczania bieżącego czasu lotu na odległość samolotu od pasa, x(t), i vice versa: t(x). Funkcja x(t) to przecałkowana po czasie pozioma składowa prędkości samolotu względem ziemi. Szacuje się ją z TAS (True Airspeed) plus odpowiedniej składowej prędkości wiatru, czyli pośrednio, m.in. z IAS (Indicated Airspeed) rejestrowanej  w FDR i QAR-ach (o szczegółach wspomnę poniżej, bo z tego korzysta większość metod rekonstrukcji trajektorii).

Posłużę się tu ilustracją z bardzo dobrej pracy pana Michała Jaworskiego. Uzyskał on dobrą zgodność pofalowanej trajektorii z metody nr. 1, z trajektorią obliczeniową używającą alarmów TAWS i wartości przyspieszenia nz(t) opublikowanych przez komisje.

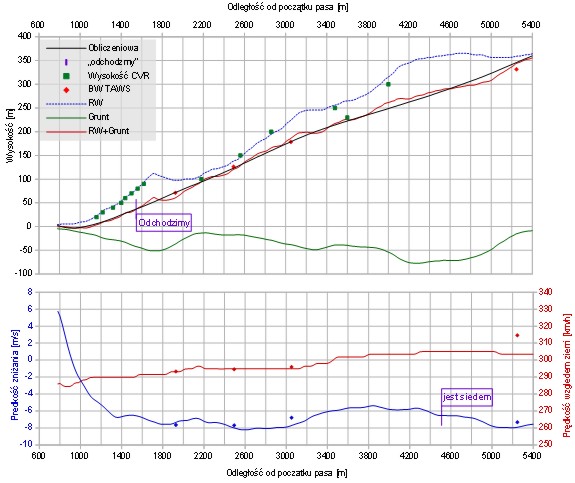
Rys. 3. Trajektoria pionowa obliczona na dwa sposoby. Metoda nr. 1 na mojej liście dała trajektorię czerwoną (źródło: Michał Jaworski) . http://planets.utsc.utoronto.ca/~pawel/pix/traj_pion_npv33.jpg

Skąd biorą się lokalne zagięcia trajektorii wyznaczonej z RA/RW? Na przykład linia czerwona na rys. 3 ma wznoszący kierunek w odległości 1800m od pasa, gdzie z innych źródeł, np. alarmu TAWS37 wiemy, że samolot opadał, a nie wznosił się, i to bardzo szybko, pomiędzy 7 a 8 metrów na sekundę! Zamiast niepokojąco dużgo opadania, można lokalnie dostać niefizycznie szybkie wznoszenie (krzywizna trajektorii jest tam większa, niż podczas spóźnionej, energicznej próby ratowania życia przez pilotów, parę chwil później). Gdyby ten fragment rekonstrukcji znajdował się w dużej odległości od pasa, to dziwny wynik mógłby w zasadzie być efektem niewłaściwego tłumaczenia czasu na odległość, gdyż  x(t) w miarę całkowania prędkości traci dokładność. Ale to nie dotyczy odległości 1800m przed pasem. 

To problem głównie niedokładnej znajomości ukształtowania terenu, która ma swą rozdzielczość przestrzenna wzdłuż ścieżki schodzenia (na ogół > 100 m, w mniejszej skali dane są interpolowane). RA(x) ma większą rozdzielczość i dokładność. Piloci lądując w systemie instrumentalnym ILS wyższych kategorii posługują się za markerem wewnętrznym, tuż przed lądowaniem radiowysokościomierzem, także rutynowo wykorzystywany był przez wszystkich pilotów tupolewów do gładszych przyziemień. Nad gładkim terenem dokładność wyznaczenia wysokości RA jest lepsza niż 1 m! Zatem większość zafalowań i uskoków na wynikowej trajektorii w metodzie 1 odzwierciedla zestawianie mniej dokładnej mapy terenu z wyższej dokładności wysokością radiową. Desynchronizacja wyliczanej i prawdziwej odległości samolotu na mapie, w danej chwili czasu, stanowi też pewien problem. Uważny czytelnik zauważył może, jak rozjeżdżają się funkcje H_rez(x) = z(t) - RA(t(x)), wyliczone z trajektorii z(t) liczonej z dynamiki lotu oraz bardziej prawdziwe H(t) z kartografii GiS, na rys. 46 MAK-u.. Górki i dołki są podobne, ale nie są w tym samym miejscu x. 

2.   Alarmy systemu wczesnego ostrzegania TAWS

Gdyby TAWS zapisywał położenia (z GPS) dostatecznie często, oznaczając je czasem uniwersalnym, byłby to bezpośrednio uzyskany, poszukiwany wykres trajektorii wraz z zależnością czasową ruchu po niej. Ale TAWS nie zapisał położeń dostatecznie często, tylko generując nowe alarmy, i to obarczone typowymi zakresami błędów GPS-a. Mamy na zniżaniu punkty TAWS 34-38, przy czym punkt 38 leżał już za brzozą. Nota bene, wszystkie są wydrukowane w załączniku 4 raportu "Millera" KBWLLP, strona C-1 do C-9, protokół odczytów UASC (to podaję gdyby gdyby ktoś uwierzył w kłamstwo podkomisarza Nowaczyka, że TAWS 38 komisja Millera ukryła), Dalej zajmiemy się już tylko mniej geometrycznymi a bardziej dynamicznymi metodami. TAWS-y wykorzystamy do ich sprawdzenia a posteriori.

3.   Rejestrowane przyspieszenie pionowe i prędkość: n_z(t) i IAS(t)

3.1.  Prosta ilustracja metody i jej problemów

Pierwsza wykorzystywana poniżej wielkość (n_z lub nz) to czynnik obciążenia (przyspieszenia pionowego względem kadłuba) podawany w jednostkach g = 9.81 m/s². Druga to v(t). Pod tym oznaczeniem kryje się TAS (prawdziwa). IAS (prędkość instrumentalna) nie nadaje się do odtwarzania kinematyki, odwrotnie niż do dynamiki. Przeliczanie znanego z rejestratorów IAS na nieznany TAS to oczywiście cenna dla  każdego badacza umiejętność, zwłaszcza na dużej wysokości, gdzie iloraz v_TAS/v_IAS = (ρ_std/ρ)^1/2 jest sporo większy od jedynki. To nie jest mała poprawka, kiedy samolot leci względem powietrza TAS=800 km/h, a na szybkościomierzu i w czarnej skrzynce ma IAS=550 km/h. Ale nie będę tu rozpraszał detalami, tak czy owak musimy umieć dość dokładnie tłumaczyć IAS na TAS przy użyciu modelu atmosfery, jej zmiennej z wysokością gęstości (lub temperatury i ciśnienia atmosferycznego). Na małych wysokościach TAS~IAS i tam używam modelu eksponencjalnego, ρ = ρ_lotniska exp(-z/const.)

Użycie n_z zilustruję najpierw dla przypadku szczególnego: samolotu lecącego ze stałym, zerowym pochyleniem (θ_p=0) kadłuba. Mierzone przyspieszenie (g n_z) powierzchniowych sił aerodynamicznych i przyspieszenie g objętościowej siły grawitacji działają wtedy wzdłuż tego samego kierunku i mamy proste równanie ze znanym n_z(t):

v_z(t) = ∫^t g [n_z(t) - 1] dt + v_z0.                                                                     (1)

Nie wypisuję explicite dolnej granicy całkowania po czasie t=0, i nie czynię literowego rozróżnienia między górną granicą całkowania t, a zmienną całkowania t. Stała v_z0 to v_z(t=0).  Następnie robimy drugie całkowanie, by z prędkości pionowej wydedukować wysokość

z(t) =  ∫^t v_z(t) dt + z₀                                                                                  (2)

gdzie wys. początkowa z₀= z(t=0) to stała całkowania, determinująca jak wysoko nad pasem zawieszony jest kształt trajektorii określony przez całkę oznaczoną. 

I w tym miejscu już widzimy jak czuły będzie nasz kształt trajektorii z(t) lub z(x) na przyjęte v_z0 i dokładność nz(t). Całkowanie (1) zgodnie z równaniem (2), daje jako drugi składnik iloczyn v_z0t. Gdy całkujemy przez parę sekund, nie ma problemu, ale gdy zakres t obejmuje aż dwie minuty lotu, to nawet +-0.25 m/s niepewności w początkowej prędkości pionowej, czyli lokalna odchyłka kąta nachylenia trajektorii o ok. 0.003 radiana bądź 0.17 stopnia, daje duży błąd +-30m wysokości końcowej. Nikt nie zna początkowych chwilowych kątów nachylenia trajektorii z wyższą dokładnością,  jest więc potencjalnie jeszcze gorzej. Podobnie, mikroskopijna (wydawałoby się) systematyczna odchyłka δn = +0.003 g = 0.03 m/s² w wartościach n_z(t),  da aż  δn t²/2 ~ +0.03(120s)²/2 m = +216 m odchyłki w wysokości! (Nota bene, dane ATM QAR miały taki niezauważony początkowo przez nikogo, systematyczny błąd kwantyzacji, którego nie miał MSRP64). Metoda nr. 3 nie jest więc pozbawiona, mówiąc delikatnie, trudności. To nieodłączna zmora podwójnego całkowania, że tak powiem, odrobinę dramatyzując. 

W kierunku poziomym, znamy v_IAS(t) i zmieniamy na TAS, aby w końcu dostać ostateczną szybkość względem ziemi v(t), zgodnie z naszą wiedzą o wietrze w danym miejscu i na danej wysokości (zakładam zwiększenie wiatru o prędkości 3 m/s i kierunku 120, jak w komunikacie radiowym wieży,  o czynnik dwa na wysokości 1 km). Możemy napisać, oznaczając kąt wznoszenia przez θ, 

x(t) = ∫^t v(t) cosθ dt + x₀ .                                                                                            (3)

Gdy mówimy o x(t) i z(t), mamy na myśli położenie środka masy samolotu.  Wartość cosθ jest bliska 1, ponieważ dla θ <<1 mamy cosθ = 1 - θ²/2 ~ 1.

Jeśli jednak trajektoria nie jest w wystarczającym przybliżeniu pozioma, to nie problem. Poprawiamy dokładność x(t) wyznaczając v_z z równania (1), a wartości θ z trygonometrii: 

θ  = arcsin(v_z/v_TAS).                                                                               (3b)

Mając policzone (2) i (3), możemy na komputerze wykreślić z(x)  w funkcji x, co zamyka rozwiązanie problemu znalezienia trajektorii z(x) w postaci parametrycznej: z= z(t), zaś x = x(t), od punktu początkowego analizy do końcowego. Początkiem będzie czas dwóch minut przed utratą końcówki skrzydła, a dokładniej t=8:39:00.00 wg FDR/QAR, końcem natomiast będzie t₁=8:40:59.36, kiedy samolot stracił 1/3 rozpiętości lewego skrzydła na brzozie.

Konieczne stałe wyznaczamy z warunków początkowych i końcowych:

(i) wiemy gdzie stała brzoza Bodina, 853 m od pasa wzdłuż kierunku x, co da nam po zakończeniu całkowania równania (3) x₀ . Dla prostoty przyjmiemy nieco inną konwencję: x₀ = 0 w momencie początkowym t=0  i będziemy kontynuować analizę do czasu t₁, tj. do t₁= 119.36 s = (8:40:59.35)-(8:39:00.00), i przesuwać trajektorię w poziomie, by zakończyła się  dokładnie w czasie t₁ na linii brzozy (jak się okaże, punkty początkowe będą się różniły w różnych metodach rekonstrukcji tylko o 9-14 m. 

(ii) wiemy też, że samolot zniżył się na minimalną wysokość środka ciężkości około z_min = -3.5 m pod poziomem pasa startowego. Za tym punktem, wznosząc się nad ziemią, ciął  gałęzie na wysokości -5 m nad pasem (por. raport KBWLLP). Różnica wysokości skrzydeł i środka masy to około 1.5 do 2 m, w zależności od pochylenia kadłuba, a że pochylenie znamy z rejestratorów, można to dość dokładnie uwzględnić. Brzoza uderzona została przez skrzydło wg KBWLLP na wysokości 1.1 m nad pasem startowym (tab. 2 na str 4/14 Zał. 4 do rap. końcowego), więc weźmiemy jako końcowe położenie samolotu przy brzozie Bodina z₁= z(t₁) = 3 m nad progiem pasa.

3.2. Uogólniamy metodę

Omówiłem do tej pory prosty, lecz nierealny przypadek, kiedy samolot leci niepochylony (pitch = 0, albo θp=0). W istocie, znamy dobrze historię kąta pochylenia z FDR do którego podłączony jest żyroskop o nominalnej dokładności 0.1 stopnia. Można więc śmiało uogólnić równania na przypadek lotu w pochyleniu. Zamiast, jak poprzednio, rzutować wektory przyspieszeń różnego rodzaju na oś pionową, aby zobaczyć co wchodzi do wyrażenia na nz, będziemy teraz rzutować przyspieszenia na oś 'pionową' samolotu ustawioną pod kątem θp do kierunku grawitacji. Grawitacja jako siła objętościowa, ani siła ciągu  M f_P, nie wpływają na pomiar nz, jedynie siła nośna o przyspieszeniu f_L i siła oporu formy i indukowanego, dająca przyspieszenie f_D (wskaźnik D oznacza opór, ang.: drag). Przyspieszenia siły nośnej i oporu są ułożone na osiach układu skierowanego wzdłuż stycznej do trajektorii, przechylonego w stosunku do osi kadłuba o niewielką liczbowo różnicę pochylenia kadłuba θp i kąta wznoszenia trajektorii θ, czyli o mały kąt 

Δ := θp - θ,                                                                                                 (4)

który jest prawie tym samy co kąt natarcia. Różni się od kąta natarcia skrzydła tylko wartością kąta zamocowania jego cięciwy (AOA = Δ + α_fix  = Δ + 3^o). Ciąg silników f_P nachylony jest do prawdziwego pionu o kąt prosty minus θ_p, a do "pionu" bryły samolotu o kąt prosty (tak zakładamy; w istocie kąt jest odrobinę inny, ale bardzo mało różny, i nie wpływa to na wyniki).  Rzutowanie wektora  fL+fD +fP na oś pionową samolotu daje następującą wartość czynnika obciążenia n_z mierzonego przez akcelerometr samolotu: 

g nz =  cos(θp-θ)  f_L + sin(θ_p-θ) f_D  =   cosΔ f_L + sinΔ f_D                            (5)

co zapiszemy inaczej  jako użyteczne wyrażenie na przyspieszenie siły nośnej 

f_L =  secΔ g nz  + tanΔ f_D ,                                                                      (6)

gdzie  wartość przyspieszenia sił oporu aerodynamicznego jest ujemna:

f_D = -C_D  (ρ v2/2)(A/M),       gdzie  A = 200 m2,    M = 79000 kg,         (7)

zaś wartość siły nośnej dodatnia i różniąca się od f_D tylko współczynnikiem bezwymiarowym:

f_L = -C_L (ρ v2/2)(A/M).                                                                              (8)

W równ. (7) i (8) możemy przyjąć gęstość standardową ρstd = 1.225 kg/m3 oraz v=IAS, albo, z tym samym skutkiem, lokalną gęstość właściwą dla wysokości lotu i  v=TAS. Zachodzi bowiem równość ciśnień dynamicznych mierzonych rurką Pitota,  ρstd (IAS)2/2 =  ρ (TAS)2/2 .  Napracowałem się tu opisując jak obliczyć przyspieszenie fL z danych o nz(t) w równaniu (6), i prędkości v_IAS(t) w równaniu (8), gdyż f_L będzie niezbędne m.in. w równaniach ruchu uogólniających równ. (1) i (2).

Jedyne, czego nie opisaliśmy do tej pory, to jak wyznaczyć współczynniki aerodynamiczne siły nośnej i oporu. Na pomoc przychodzi standardowa teoria skrzydła skończonego o rozpiętości b i polu powierzchni górnej A, która mówi, że do C_D wnosi wkład stały współczynnik oporu formy C_D0, oraz oporu indukowanego, zależnego od kąta natarcia skrzydła (np. Basic Wing and Airfoil Theory, Alan Pope, Dover 2009)

C_D = C_D0 + C_L² /(π AR ε),                                                                            (9)

gdzie wydłużenie płata oddaje tzw. aspect ratio AR = b2/A, równy AR=7.11 w tupolewie 154M. Parametr ε można tu przyjąć równy jedności. To prosta teoria, która ma tendencję do pewnego zawyżania C_D. W podręczniku Behtira i in. (1997)  "Praktyczna aerodynamika samolotu TU-154M" można odwołać się do rys. 1.5 pokazującego C_D i C_L w funkcji kąta natarcia. W konfiguracji na podejściu 10.04.10  CL powinno być rzędu jedynki a C_D0 około 0.16,  jednak w praktyce stała i niezależna od pochylenia wartość C_D0 jest nieco wątpliwa. Ja brałem C_D0 = 0.13, a wynikowy C_D był przez większość czasu zbliżony do 0.16, wartości działającej też nieźle w problemie balansu sił podłużnych, który tak tu skonfudował jednego(?) z blogerów.

Pora teraz zapisać  zwyczajne równanie różniczkowe na ruch w pionie,  jako rzut sumy wektorowej przyspieszeń działających na samolot (g + f_L + f_D + f_P) na oś pionową:

dv_z/dt  = -g + cosθ f_L + sinθ f_D + sinθ_p f_P.                                                   (10)

Stąd, korzystając z równania (6), dostaniemy zasadniczo inną formę równania, odwołującą się do zapisu n_z zamiast do postaci funkcji C_L w f_L:

dv_z/dt = g (n_z cosθ secΔ  -1)  + (sinθ - cosθ tanΔ) f_D +   sinθ_p f_P  .              (11)

Wraz z równaniem (3), jedno z dwóch równań dynamiki, (10) lub (11), daje trajektorię. Człony odpowiadające sile oporu i ciągu są bardzo małe w porównaniu z pozostałymi, rzędu pochylenia samolotu i trajektorii (w radianach), razy stosunek tych sił do ciężaru samolotu, w sumie (tzn. iloczynie:) typowo tysiąc razy mniejsze niż g. Jednak tutaj, wbrew nawykom fizyka, to istotne by zawsze włączać małe poprawki (zob.: zmora podwójnego całkowania w rozdz. 3.1), dopóki nie udowodnimy że nie są istotne.

4. Metody całkowania szybkości zmian nachylenia trajektorii  

Zamiast mówić o kartezjańskiej składowej wektora prędkości, vz, możemy przejść do układu biegunowego (v_TAS, θ) i zapisać w szczególnie prostej postaci jak szybko zmienia się w czasie kąt nachylenia wektora prędkości, θ(t). Rzutując siły: nośną, ciągu silników i grawitacji na kierunek trajektorii (opór nie wnosi wkładu) dostajemy

v_TAS dθ/dt = -g cosθ  + f_L + sinΔ f_P  ,                                                          (12)

Używając równania (6) zastępujemy fL przeciążeniem pionowym, kosztem wprowadzenia małych poprawek od sił oporu aerodynamicznego i napędu: 

v_TAS dθ/dt = g (nz secΔ - cosθ) - tanΔ f_D + sinΔ f_P  .                                    (13)

Rozwiązaniem problemu jest trajektoria dawana przez równania (2) i (3), gdzie

vz(t)= v_TAS(t) sinθ,                                                                                       (14a)

θ(t) = ∫^t  (dθ/dt)  dt  + θ₀ .                                                                           (14b)

Tutaj naturalnie podstawiamy (dθ/dt) albo z (12) albo z (13). Jest to wygodna odmiana metody podwójnego całkowania przyspieszeń.

Na koniec zauważmy, że w każdej metodzie przechodzącej od przyspieszeń do prędkości, i dalej do położeń, będziemy mieli możliwość zmiany nie tylko położenia w płaszczyźnie (x,z) uzyskanej trajektorii, ale i jej kształtu, przy użyciu zmian stałych całkowania na tyle małych, by były niesprzeczne z precyzją tych wielkości w realnych pomiarach. To i dobrze i źle. Dobrze, bo tak można walczyć ze zmorą rozjeżdżania się teorii i niezależnie zebranych danych. Niedobrze, gdyż ta giętkość metody przypomina dopasowywanie funkcji matematycznej o wielu parametrach swobodnych, zabawa szalenie miła, lecz nie zawsze pouczająca.  

5. Metody półalgebraiczne  

Moim osobistym faworytem jest ta metoda, którą sobie wymyśliłem, podejrzewam że nie jako pierwszy. Ma mniej parametrów swobodnych, w zasadzie oprócz translacji na mapie (x,z) nie można w niej zmienić prawie nic w kształcie trajektorii uzyskanej z pomiarów zapisanych w rejestratorach. To takie pójście po bandzie: jak się nie uda (tzn. jeśli niezależne dane nie będą pasowały do wyników modelowania dynamiki) to trudno, ale jak się uda, to da dużo większą pewność, że znamy prawdziwą trajektorię, a nie  tylko jeden z nieskończonej rodziny wielu kształtów, najlepiej pasujący do obserwacji. No ale to bardziej moja estetyka naukowa niż dowód. The proof is in the pudding, zatem bierzmy się do jego robienia.

Wiemy o aerodynamice tak dużo, że pozwala to zredukować rząd równań różniczkowych o jeden, zmniejszając krotność całkowania i  tym samym zmniejszając czułość trajektorii na narastanie błędów systematycznych w długich okresach czasu. Weźmy pod uwagę współczynnik C_L(α) potrzebny do obliczenia f_L zgodnie z równaniem (8).  Zależy on od kąta natarcia α = AOA, który równy jest [por. np. 49. rozdział bloga o kącie natarcia]

α = θp  -  θ  + α_fix    =    Δ + α_fix                                                                (15)

gdzie ostatni kąt po prawej stronie to kąt mocowania cięciwy skrzydła na kadłubie (+3^o). Na podejściu przed brzozą Bodina, wg podręcznika Behtira i wielokrotnie robionych przez różne grupy badań w tunelu aerodynamicznym, kąt α jest na tyle mały, że współczynnik siły nośnej CL zależy od niego liniowo:

CL(α) =  C_Lα  (α - α₀)                                                                                 (16)

gdzie α₀ = -5.4^o jest kątem natarcia pod którym skrzydło z klapami wysuniętymi na 36^o produkuje zerową siłę nośną, zaś  stała C_Lα = 5.46 to empirycznie wyznaczone, podręcznikowe nachylenie charakterystyki TU-154M, mniejsze od teoretycznego maksimum 2π dla idealnego płata nieskończonego (por. teorie Kutty i Żukowskiego z początku 20. wieku). Ta wartość jest używana z kątami α wyrażonymi w radianach. Wstawiając (15) do (16), i używając definicji kąta Δ  możemy napisać w wygodnej formie  liniowej 

C_L(Δ) = C_Lα (Δ - α₀ +α_fix) .                                                            (17) 

Teraz, kiedy pewnie wszyscy już zasnęli, zaczyna się robić cholernie ciekawie (pierwsze trzy osoby które dotrwały, zapraszam w nagrodę na lot pod Golden Gate bridge w SF, gratuluję i proszę o kontakt). Wyznaczymy kąt Δ w każdej chwili czasu wprost z danych parametrycznych PLF 101.  Mając do dyspozycji historię prędkości v_IAS, znamy przyspieszenie masy M pod działaniem siły oporu dynamicznego (ram pressure) na powierzchnię prostopadłą A, co skrótowo zapiszemy jako 

 a_ram (v_IAS) = (ρ_stdv²_IAS/2) (A/M).                                                              (18) 

Tę wielkość odnajdujemy w równaniach (7) i (8) na przyspieszenia aerodynamiczne. Przyrównując (6) i (8) i uwzględniając też (7) i (17), otrzymujemy bezwymiarowe równanie algebraiczne, gdzie niewiadomą jest poszukiwana przez nas Δ:

g n_z/a_ram  =   cosΔ [tanΔ  C_D(Δ)  + (Δ - α₀ +α_fix)C_Lα ].                             (19) 

Nieliniowa zależność C_D od Δ dana jest równaniami aerodynamicznymi (9) i (17), a lewa strona równania jest znana z zapisów n_z i v_IAS  w locie PLF101.  Zauważmy, że znów siła oporu jest tylko małą poprawką, gdyż jest mnożona przez tanΔ ~ Δ <<1 ,  przy kątach  Δ rzędu jednego stopnia. Pomijając pierwszy składnik w kwadratowym nawiasie, dostajemy z równania (19) pierwsze, niezłe przybliżenie na Δ, które już daje dobre przybliżenie trajektorii. Możemy je poprawiać iteracyjnie, biorąc do obliczenia drugiego przybliżenia Δ wartość C_D  z pierwszego przybliżenia Δ, itd. Po czterech iteracjach wynik ustala się na poziomie sześciu cyfr znaczących i dostajemy Δ(t), a poprzez

θ = Δ - θ_p                                                                                                    (20) 

także nachylenie trajektorii w funkcji czasu. Bez całkowania, algebraicznie. Dalej tak jak zawsze, musimy raz przecałkować równanie (2) z  prędkością pionową z (14a), i koniec pracy. Porównamy teraz wyniki paru opisanych metod rekonstrukcji trajektorii.

  REKONSTRUKCJA KĄTÓW i PRĘDKOŚCI ZNIŻANIA

Skan o rozdzielczości czasowej 1s z raportu MAK, wartości w dwóch ostatnich minutach lotu: pochylenia samolotu, nz, prędkości instrumentalnej vIAS i rejestrowanego kąta natarcia AOA, który użyję do porównania z wyliczonym,  otrzymałem od Michała Jaworskiego. Bardzo dziękuję. Popatrzmy na rys. 4. Jeśli komuś zdaje się że jest tam za dużo krzywych, powiem, że początkowo wykreślałem tam jeszcze i trajektorie :-). Na osi poziomej jest czas w sekundach zaczynając od okrągłej minuty zapisu MSRP64 i QAR. Pionowa linia przerywana w t=119.36 to koniec rekonstrukcji, inaczej - brzozy. Dalej założenia rekonstrukcji nie są spełnione, gdyż przyjmujemy poniżej, że samolot nie był przechylony.

Pierwsza od góry to krzywa nz(t); wartość n_z=1 pokazana jest linią przerywaną, a mała podziałka na osi pionowej to różnica nz równa 0.125. Tuż pod nią widać stosunkowo mało ważną funkcję siły ciągu podzielonej przez ciężar samolotu. Ale skoro tyle się napracowałem dygitalizując ją... Poniżej kropkowanej osi oznaczającej zerowy kąt, widzimy łososiową krzywą pochylenia samolotu (w tym niestety sporą kwantyzację jej poziomów we Flight Data Recorder, MSRP64). 

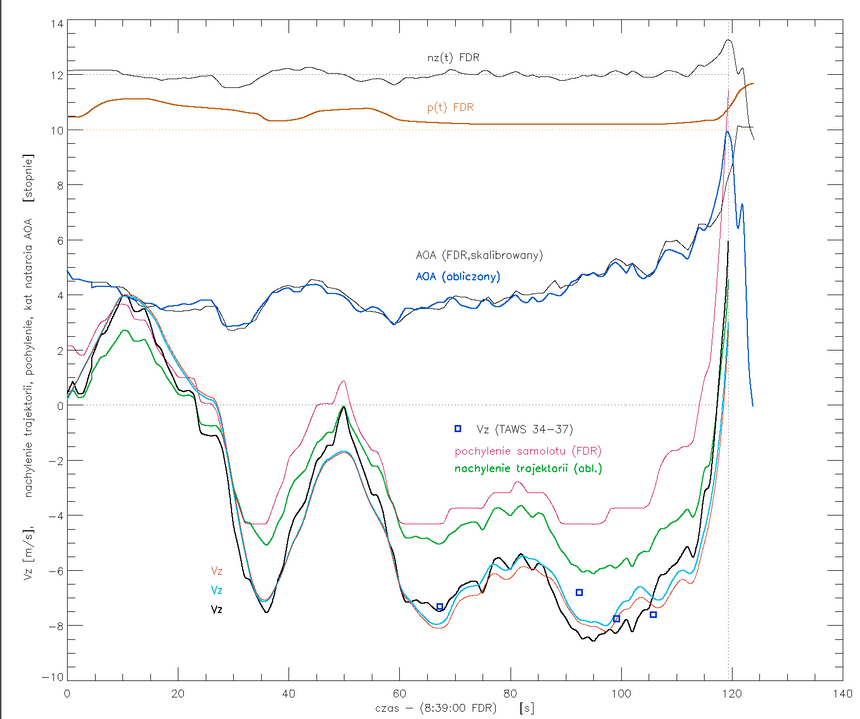
Rys. 4. Wykresy kilku zależności czasowych z rejestratorów lotu PLF 101, oraz wartości wyliczonych omówionych w tekście. Pochylenie pochodzi z raportu MAK; nachylenie trajektorii zostało obliczone algebraicznie (iteracyjnie). Trzy najniższe krzywe to prędkości pionowe w m/s, w trzech metodach rekonstrukcji opisanych w tekście. Zgadzają się dokładnie z prędkościami opadania zapisanymi w alarmach TAWS 34,36,37, i nie najgorzej (15-20% wartości) z TAWS35, który był też punktem najgorzej zgodnym z analizą MAK (por. rys. 1).  W wyższej rozdz.:  http://planets.utsc.utoronto.ca/~pawel/pix/fig21-3-.png.  

Moim zasadniczym modelem obliczeniowym była metoda półalgebraiczna. Zielona krzywa to nachylenie trajektorii θ(t) zrekonstruowane iteracyjnie wg tej procedury z podrozdz. 5. Krzywa leży przez większość okresu zniżania ok. 1 stopnia poniżej krzywej pochylenia kadłuba. To znaczy, że mimo iż kadłub i trajektoria zmieniały tam znacznie ustawienie względem horyzontu, w zakresie -6 do +4 stopni, to kadłub był ustawiony pod prawie niezmiennym kątem Δ do trajektorii. Po dodaniu do Δ kąta α_fix = 3^o dostajemy niebieską krzywą obliczonego kąta natarcia. [Nota bene, pisaliśmy to z p. Jaworskim w dwóch notkach o oszustwie podkomisji Macierewicza w związku z badaniami tunelowymi i ich pozbawioną sensu teorią, że przy brzozie kąt natarcia był mały a tupolew był w przypadku utraty skrzydła sterowalny. Podkomisja twierdzi to na podstawie swej "wiedzy", że kąt natarcia miał wartość ok. 5^o. Na rys. 4  widzimy kąt natarcia na pionowej linii przerywanej (moment utraty skrzydła). Ani obliczony, ani skalibrowany kąt natarcia mierzony urządzeniem tupolewa nie jest w żadnym sensie mały. Wynosił 10-12 stopni, więc w sposób oczywisty samolot był niesterowalny i jego obrotu w półbeczce nie można było w żaden sposób uniknąć.]

Jak anonsowałem wcześniej, także w poprzednich notkach takich jak ta, na podstawie aerodynamiki płatowca oczekujemy, że kąt natarcia na podejściu jest mniej więcej stały. To wie z praktyki każdy pilot. Np. ciągiem silnika zmieniamy nachylenie trajektorii i pochylenie samolotu, ale nie AOA i prędkość lotu - w każdym razie niewiele. Zmiany AOA (wywołane m.in. częstym trymowaniem samolotu kółkiem SPUSK_PODJOM) zapisały się w rejestratorach, ale wartości zapisane nie są prawdziwymi wartościami kąta natarcia. Dyskutowane było to wielokrotnie w latach 2011-2019, por. np. blog M. Jaworskiego, na podst. pracy Synicyna, gdzie prawdziwy kąt określony jest zgrubnie jako połowa kąta wskazywanego plus 3^o. Na rysunku zaznaczyłem podobnie skalibrowany kąt wskazywany przez układ skrzydełek znajdujących się tuż za kokpitem, na zewnątrz samolotu. Wartości wykreślone to

AOA(skalibrowany) = 0.4*[wskazania przyrządu(w stopniach)] +2.5 stopnia

Krzywe AOA mają dokładnie ten sam wygładzony kształt, choć nie mogą mieć dokładnie tej samej zmienności w krótkich skalach czasu. Jedna to pomiary kąta opływu kadłuba za kokpitem przez powietrze w smoleńskiej chmurze, druga to wartość obliczeniowa α=AOA gwarantująca wytwarzanie (wg aerodynamiki) dokładnie takiej siły nośnej, jaka odzwierciedlona jest w rejestrowanych niezależnie przeciążeniach. 

Krzywe prędkości opadania v_z(t) są zbliżone do siebie i ogólnie zgodne z rekonstrukcją MAK. Czarna linia pokazuje rekonstrukcję z podrozdziału 5, czerwona z paragrafu 4, a niebieska z podrozdz. 3.2.

Wszystkie wyniki zgadzają się ze znanymi wnioskami dotyczącymi błędnego pilotażu na podejściu nieprecyzyjnym do pasa 26. Prędkość opadania dochodziła do (i chwilowo przekraczała) 8 m/s. Prawidłowe, ustabilizowane podejście przewiduje 3.5 do 4 m/s. Ciekawie zobaczyć gdzie leżą na wykresie te wartości! Jednocześnie widzimy wielkie, wygaszane w miarę lotu zafalowania prędkości zniżania. Sugeruje to, że wkład w dynamikę lotu tupolewa prezydenckiego mógł dawać wzbudzony w dniu wypadku długookresowy mod oscylacji, odchyleń od równowagi podłużnej, tzw. fugoida. To temat przyszłego rozdziału bloga.  

 REKONSTRUKCJA TRAJEKTORII

W ostatnich dwóch minutach lotu pochylenie samolotu zmieniało się silnie, częściowo poprzez trymowanie wykonywane przez pilotów. Podążały za tym zmiany θ i garby na trajektorii, które widzimy wyraźnie na rys. 5. Ostatni i najmniejszy z nich znajdował się w odległości ~3 km od pasa, gdy samolot był na wysokości 150-200 m BW. Gdyby utrzymano mniejszą prędkość opadania, jak po lewej stronie garbu, trajektoria trafiłaby prawie w początek pasa. Zagięcie trajektorii w dół spowodowało, że ostateczna granica dopuszczalnego zniżania (MDH=100 BW) została przestrzelona w sposób bardzo jaskrawy.

Zabrakło jakiejkolwiek komendy o rozpoczęciu odejścia zarówno na 120 m nad pasem (legalne minima pilota) jak i na MDH (błędnie odczytane przez analityków CLKP i powtórzona dosłownie przez panią mgr X z krakowskiego IES fraza "Odchodzimy na drugie [zajście(?)]" wypowiedziana jakoby w 0.5s pomiędzy dwoma znacznikami sub-ramki, zawsze niemożliwa fizjologicznie, była błędnie odczytana. Obecnie, wg opinii kompleksowej zespołu biegłych prokuratury krajowej, ta fraza brzmi "Dochodź wolniej", co było ostrzeżeniem dla pilota lecącego. A co najważniejsze, przy przekraczaniu legalnej i bezpiecznej wysokości MDH zabrakło jakiejkolwiek akcji pilotów, która zapisałaby się na wykresach położenia kolumny sterowej tupolewa.

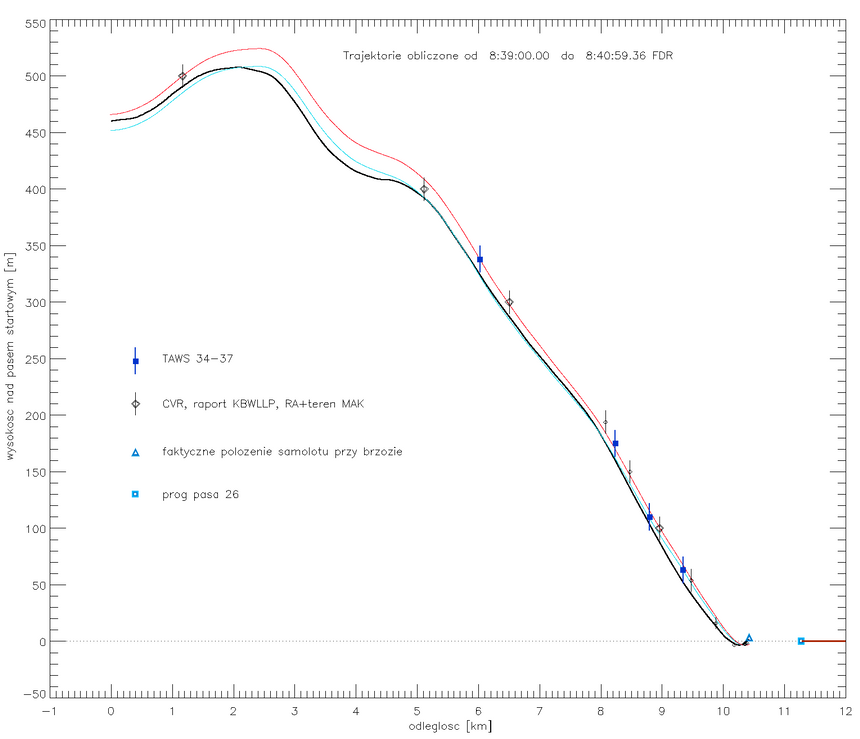
Rys. 5. Trzy trajektorie obliczone różnymi metodami opisanymi w tekście. Iteracyjna metoda pół-algebraiczna to krzywa czarna. Krzywa czerwona to metoda z podrozdz. 4, a niebieska z podrozdz. 3.2. Rys. w wyższej rozdz.:  http://planets.utsc.utoronto.ca/~pawel/pix/fig21-4-.png

Zaznaczyłem na rys. 5, dla porównania, kilka punktów z pamięci TAWS i punktów opisanych w raportach komisji, wraz z zakresem 1σ błędu pomiarów. Uwzględniając jak długi jest zakres czasowy rekonstrukcji, określiłbym zgodność wszystkich trajektorii z tymi punktami jako bardzo dobrą (statystycznie zgodną z zakresem nieoznaczoności, i pozbawioną większych efektów systematycznych, chociaż można określić główną trajektorię (czarną) jako leżącą generalnie pod punktami TAWS i niektórymi innymi zaznaczonymi. Nie ma gwarancji czy rejestrowane wartości TAWS nie miały niewielkiej składowej błędu systematycznego ~10 m (odchyłki od geoidy, ograniczona liczba widocznych satelitów GPS itd, por. niedawny blog stanzaga). Jeżeli taka składowa była, to mogła zawyżać nieznacznie wysokość samolotu nad pasem w alarmach TAWS. Dlaczego jednak przywiązuję największą uwagę do metody rekonstrukcji nr. 5, wykreślonej na czarno? Popatrzmy na część trajektorii poniżej 200 metrów nad pasem:

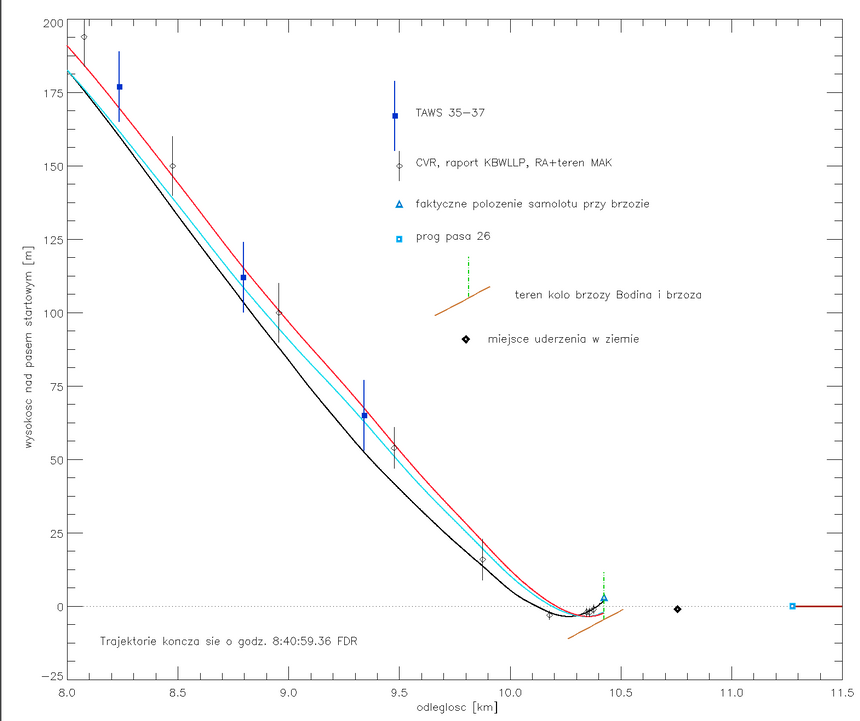
Rys. 6. Rekonstrukcje końcowego podejścia w okolicy brzozy, uderzając w którą PLF 101 stracił końcówkę skrzydła, będąc w położeniu  zaznaczonym trójkątem, dużo poniżej czubka 16-metrowej brzozy. Stamtąd samolot leciał niesterowny, w rosnącym przechyle do zaznaczonego punktu, znajdującego się ponad pół km od progu pasa 26 lotniska Siewiernyj. Kolory linii jak na poprzednim rysunku. http://planets.utsc.utoronto.ca/~pawel/pix/fig21-5-.png

Największe zbliżenie sytuacji koło brzozy, gdzie można już zobaczyć różnice modeli położeń w decymetrach, pokazuje poniższy rys. 7. Na rys. 6 i 7 na brązowo zaznaczony jest teren gruntu, który koło brzozy na działce Bodina miał wysokość -4.5m nad progiem pasa i nachylenie średnie 1:25 (2.3 stopnia). Przypominam, że wszystkie punkty początkowe trajektorii leżały na takich wysokościach, by odtworzyć minimalną wysokość -3.5 m nad pasem znaną mniej więcej z historii przycinania drzew przed działką lekarza Bodina i jego brzozą (Zał. 4, raport KBWLLP). W poziomie trajektorie inne niż czarna są przesunięte o 9 i 15 m w lewo, w stosunku do tych które były liczone startując z tego samego x=0 w obliczeniach (to drobne, trudne do zauważenia na wykresie różnice!). 

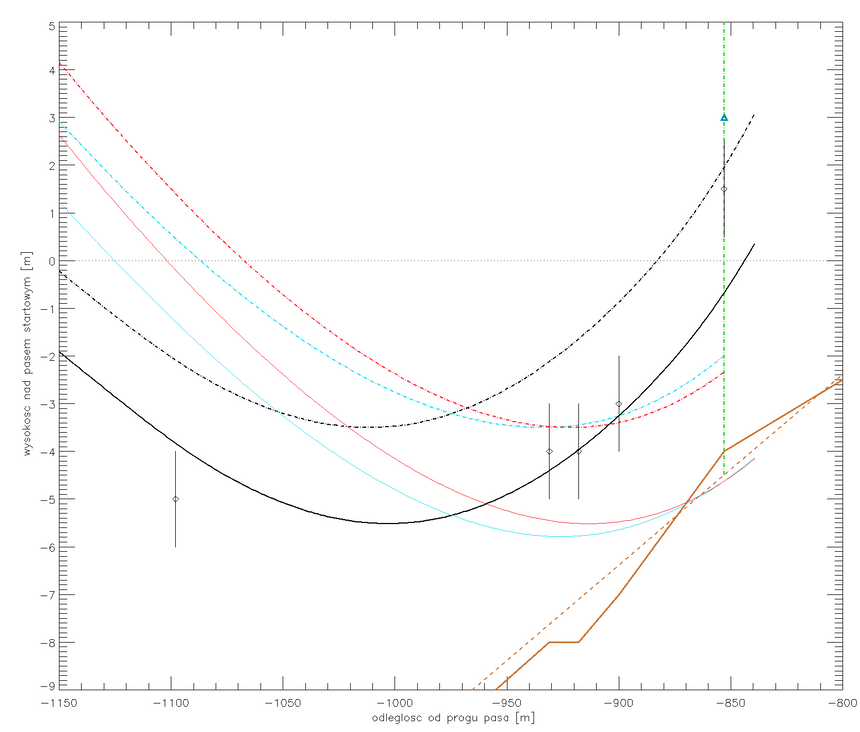
Rys. 7. Zbliżenie trajektorii obliczonych w okolicy brzozy Bodina (zielona). Symbole i kolory linii jak na poprzednim rysunku. Wyjątek: trajektorie środka masy samolotu w trzech rekonstrukcjach pokazane są liniami kropkowano-kreskowanymi. Czarna trajektoria wznosi się o godz. 8:40.59.36 (przy brzozie) z prędkością +6 m/s względem pasa, inne trajektorie odpowiadają 2.7 m/s i 3 m/s. Tempo podnoszenia się gruntu pod samolotem wynosiło średnio 3 m/s;  por. brązową linię przerywaną). Liniami pełnymi pokazane są trajektorie punktu na skrzydle, który uderzył w brzozę. Dane o wysokościach przycięcia drzew (czarne symbole) oraz model ukształtowania terenu (brązowa pełna linia) pochodzą z raportu KBWLLP.  http://planets.utsc.utoronto.ca/~pawel/pix/fig21-6-.png.

Kształt trajektorii, jej końcowa wysokość nad gruntem, i prędkość wznoszenia przy brzozie Bodina były różne w trzech zastosowanych metodach rekonstrukcji, co pozwala łatwo ocenić w zestawieniu z danymi z Tabeli 2 w Zał. 4 KBWLLP o położeniu uszkodzeń na drzewach, która trajektoria była najlepsza. Była to trajektoria półanalityczna (metoda nr. 5). Tylko linia czarna jest bardzo dobrze zgodna z opisem terenu katastrofy. Inne metody są również dość dokładne: po symulacji lotu na odległości 10.4 km lokują samolot prawidłowo w locie wznoszącym, tuż ponad gruntem. Jednak na wysokości o parę metrów za małej , ok. 3 m nad gruntem i 2 metry pod progiem pasa, zamiast metr nad progiem pasa. W mniej dokładnych rekonstrukcjach pokazanych kolorowymi liniami, nie tylko same za małe wysokości, ale i kąty wznoszenia i prędkości są faktycznym problemem: Vz = +2.7 do +3 m/s. To wykluczone. Samolot nie mógł się tak poruszać. Rys. 7 pokazuje, że zaczepiłby już w tej sytuacji podwoziem i kadłubem o ziemię przy podstawie brzozy, której właściciel by zginął.

Najlepsza rekonstrukcja umieszcza natomiast środek masy o godzinie 8:40:59.36 z dużą wiernością w stosunku do realiów: na wysokości 2 m nad pasem, w miejscu gdzie podstawa brzozy stoi na gruncie -4.5m nad pasem. To jeszcze o 2 m za mało, bo brzoza była de facto uderzona i złamana 6.5 m nad ziemią,  ale nie wymagajmy zbyt wiele. Uzyskana dokładność tej globalnej rekonstrukcji  zniżania z wysokości kręgu 500m do poziomu zerowego, jest i tak fantastyczna. Co najważniejsze, nachylenie odtworzonej jak i faktycznej trajektorii jest 853 m od pasa znacznie większe niż lokalne nachylenie terenu, umożliwiając ucieczkę spod brzozy i półbeczkę, w której, jak dobrze wiemy, tupolew nie dotknął kikutem skrzydła ziemi. Ciął tylko liczne drzewa na wysokości 5-10 m nad ziemią. Samolot wznosi się w rekonstrukcji z użyciem metody nr. 5 z prędkością V_z = +6 m/s w stosunku do pasa, a ok. +3 m/s względem terenu. Dokładnie takie założenia robiłem (gdyż były konieczne do zgodności z faktami za brzozą) dokonując dokładnej rekonstrukcji trajektorii za brzozą. Również rekonstrukcja MAK podaje taką wartość V_z, w odróżnieniu od niektórych innych prób specjalistów u nas w kraju.  Niezależne rekonstrukcje trajektorii przed i za brzozą zszywają się gładko na brzozie, nie ma żadnej rozbieżności v_z. Dla mnie to bomba! 

WNIOSKI KOŃCOWE

Można różnie rekonstruować trajektorię prezydenckiego tupolewa w chmurze, gdzie przestrzelono wszelkie zakazy i limity wysokości, wlot pod poziom pasa, początek wznoszenia, aż po utratę 1/3 skrzydła na wysokości ok. metra nad progiem pasa na działce lekarza pogotowia. Jest ciekawe, że o ile rozumie się metody rekonstrukcji z uwzględnieniem małych korekt w równaniach dynamiki, które ze swej natury potrafią wyolbrzymiać błędy wartości początkowych przy symulacji trajektorii na przestrzeni paru minut lotu, to uzupełniona metoda podwójnego całkowania przyspieszeń działa zupełnie nieźle, chociaż daje niewłaściwy o parę metrów kształt trajektorii - modelowany samolot leci z za małym kątem wznoszenia i tuż przed brzozą, o 8:40:59.4 już zaczepia o ziemię. 

Najlepsze rezultaty, spektakularnie zgodne ze wszystkimi danymi o trajektorii zebranymi w alarmach TAWS, komunikatami głosowymi o wysokości barometrycznej, i położeniami przycinanych drzew, dała jedna z prezentowanych metod (podrozdz. 5), w której unika się podwójnego całkowania przyspieszeń poprzez algebraiczne rozwiązania na funkcje nachylenia i kąta natarcia, uzyskane z pomocą praw aerodynamiki.  Nie przeprowadziłem ścisłego porównania, ale trajektoria jest b. podobna do obliczonej w dobrze wykonanym i zredagowanym raporcie MAK, wkrótce po katastrofie smoleńskiej. Warto też podkreślić, że moje metody nie korzystają z historii lotu zapisywanej osiem razy na sekundę przez system MSRP64 w skrzynce MLP-14-5 wraz z kopią w rejestratorze nieopancerzonym KBL-1-1. Mimo to odtwarzają z dużą dokładnością wysokości nad terenem tam rejestrowane (np. obliczona trajektoria zaczepia o kępy drzew przed brzozą lek. Bodina).

Znów pokazaliśmy, jak prawdziwa fizyka działa, tłumaczy katastrofę i jest konieczna do jej badania. Z drugiej strony muszę powiedzieć, że oglądana przez pilota lub każdego prawdziwego badacza (z kraju czy zagranicy) zrekonstruowana, stroma, oscylująca trajektoria błędnego zniżania 10.04.10, to źródło koszmarów nocnych.

Bezpiecznych lotów!

(c) P. Artymowicz, 20 marca 2019 r.

Zobacz galerię zdjęć:

katastrofa smoleńska