Dziś rzecz o mechanice lotu płatowca i jak pozwala ona rozwikłać zagadki wszelkie, a teorie zamachowe obalić. Te wykluwające się ciągle jeszcze w głowach blogerów salonu 24. Niestety, czasy kiedy można było pośmiać się i nauczyć czegoś dawniejszych blogerów - teraz wielkich blagierów (podkomisiów smoleńskich posła A. Zamacha) - minęły i nie wrócą. Tak jak nie wróci sam poseł na fotel ministra wojny. Brak nowych teorii podkomisiów. A pióro nieużywane wysycha i skrzypi. Wezmę więc na warsztat teorię spiskową, jaka jest: teorię o mistyfikacji danych o locie tupolewa PLF 101 do Smoleńska. Po drodze, jeśli wierzyć bardzo bardzo licznym i bardzo niefachowym notkom Niegracza/Qwerty, jedno z dwojga: albo przestała działać fizyka, albo opublikowane dane z rejestratorów TU-154M wszystkie sfałszowano, wypadek upozorowano itp. Pokażę, że fizyka działała bezawaryjnie, a nick qur-cośtam czyni grube błędy w obliczeniach wszystkich trzech sił działających wzdłuż trajektorii.
"Drogi Fagocie, pokaż nam coś prostego na początek" - mówi prof. Woland w "Mistrzu i Małgorzacie" M. Bułhakowa do swojego nieziemskiego towarzysza, który, chociaż zna prawdziwie diabelską czarną magię, to rozpocznie swoje występy przed niewtajemniczoną publicznością od "prostej" sztuczki karcianej. My też zaczniemy od pokazania, jak prosto i poprawnie liczy się siły działające na samolot wzdłuż jego trajektorii, w tym przypadku ścieżki zniżania.
'Tajemnicze' siły działające na TU-154M podczas ostatniego podejścia do lądowania
Opowiadanie użytkownika niegracz brzmi pokrótce tak: Weźmy pod uwagę dwa szczególne punkty P0 i P1 na trajektorii podejścia do PLF101:
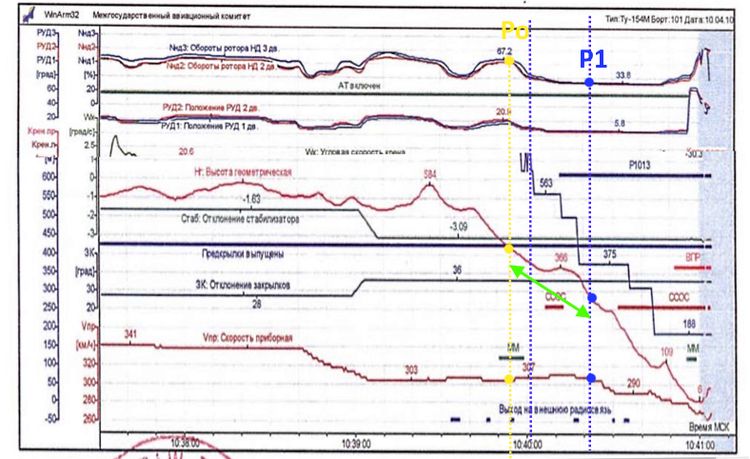
Garść danych z paru ostatnich minut zniżania feralnego lotu PLF 101 koło Smoleńska. Zdefiniowane są dwie chwile: P0 (żółta linia) oraz P1 (niebieska linia). Według teorii spiskowej, niemożliwe jest by pokazana na dole prędkość instrumentalna V(t) była taka sama w P0 i P1, co wskazuje na mistyfikację.
Przy P0 (żółta linia) działający w tupolewie automat ciągu wybrał pośrednią moc silników, co pokazują u góry rysunku obroty turbiny małego ciśnienia równe 65% nominalnych. To średnia, ponieważ są 3 nieznacznie odmienne tempa obrotów 3 turbin niskiego ciśnienia. Natomiast w punkcie P1 (niebieska linia na wykresie) automat ciągu stosował minimalny gaz w locie, który wynosi 34% maksymalnej prędkości obrotowej wspomnianych turbin. Siła napędowa wytwarzana przez silniki różniła się znacznie między tymi dwoma punktami.
Siła wypadkowa Δ działająca wzdłuż trajektorii zniżania (oś x) jest sumą następujących elementów wzdłuż tej osi:
Δ = P + G - D
G = składowa ciężaru samolotu (W = 80T, gdzie 1 T = 1 tona siły = 1000 kG),
D = siła oporu aerodynamicznego (D> 0, jest minus przed D we wzorze)
P = siła ciągu silników
Składowe będą wyrażone w tonach siły (T) zamiast w kN; współczynnik konwersji wynosi 9,81.
Teorie spiskowe ogłaszają paradoks: równowaga sił jest niezgodna z taką samą wartością prędkości w punktach P0 i P1. Twierdzą, że w obu punktach wartość G jest taka sama, a D jest prawdopodobnie nieco inna, ale w przybliżeniu stała, ponieważ kąt natarcia (AOA = angle of attack) nie zmienia się znacznie pomiędzy P0 i P1. W przeciwieństwie do prawie stałej różnicy G-D, dodatni ciąg P bardzo wyraźnie zmniejszył się pomiędzy P0 a P1. Siła wypadkowa nie może zatem być zerem zarówno w P0, jak i P1, musi być dużo mniejsza w P1 niż w P0. Jeśli Δ = 0 w P0, to Δ < 0 w P1. Przyspieszenie działające na samolot, o wartości aΔ= g (Δ/W) < 0, musi być znaczne, więc spowoduje olbrzymi spadek prędkości lotu V w ciągu> 20 sekund między P0 i P1.
Ale zarejestrowana w czarnych skrzynkach prędkość wzdłuż trajektorii łączącej P0 z P1 jest identyczna w P0 i P1, i równa się (por. raport końcowy komisji MAK)
V(P0) = V(P1) = 304 km/h = 84,4 m/s,
co jest równoznaczne z powiedzeniem, że ruch w przedziale od P0 do P1 jest jednostajny; czyli jak pokazał Galileusz, Δ = 0. Ponieważ ruch nie może być jednocześnie jednostajny i silnie spowolniony, to zapisy rejestratorów są niespójne, a cała katastrofa jest mistyfikacją. Tyle teoria spiskowa.
Sprawdźmy wpierw kluczową kwestię: jak duże są te siły i przyspieszenia. Wartości uzyskane na kontrowersyjnym blogu Qwerty można zapisać dla dwóch punktów (wszystkich sił w jednostkach T) tak:
Δ = P + G - D
0 = 16,5 + 6,8 -23,3 (przy P0)
-13,5 = 3,0 + 6,8 -23,3 (przy P1)
Hmm, lewa strona równania dla P1, siła wypadkowa Δ jest istotnie ogromna! 13,5 tony, w porównaniu z W = 80 ton samolotu daje duże opóźnienie (13,5 / 80) g = 0,17 g, które w ciągu 27 s pomiędzy P0 i P1 powinno zmniejszyć prędkość samolotu aż o 27 * 0,17 * g = 45,7 m/s = 161 km/h (!). Samolot zwali się przeciągnięty. Wygląda na to, że teoria spiskowa działa. Tylko troszkę dziwne, że pasażerów na filmie W. Lilientala z dnia 7.04.10 nie rzucało w fotelach w przód i w tył, jak w taksówce prowadzonej przez nerwowego kierowcę. Bo tam też przecież automat ciągu (choć winien być na końcowej prostej wyłączony, tak jak 7.04.10) zmieniał raptownie obroty sprężarek w górę i w dół. Co tu jest grane?!
ROZWIĄZANIE
Rozwiązanie jest proste: równanie bilansu sił było poprawne, czego nie można powiedzieć o wartościach sił wyznaczonych przez autora teorii spiskowej.
(i) Pseudo-paradoks zakłada, że ścieżka schodzenia tupolewa miała stałe nachylenie - w rzeczywistości zaś była falista i miała zupełnie inne nachylenie w punktach P0 i P1. To niezrozumienie podstaw mechaniki lotu: najczęściej zmiany ciągu są robione właśnie po to by zmienić nachylenie toru lotu, a nie po to by się wzdłuż ustalonej trajektorii rozpędzać i hamować.
(ii) Mowa tu o zafalowanym profilu wysokości barometrycznej. Qwerty pominął jednak jej analizę i mylnie wyrysowywał dane z altymetrii radarowej, w terenie którego wys. n.p.m. zmieniała się o ponad 50 m, o tę wartość zaburzając nieraz wysokość radiową.
(iii) Wartości wszystkich sił zostały źle policzone, co znacznie zawyżyło siłę wypadkową w punkcie P1 - faktycznie istnieje tam ujemna siła Δ, ale jest ona znacznie mniejsza niż ogłoszona
(iv) Założono, że prędkość jest prawie stała - a to błąd, bo mimo, iż jest równa w P0 i P1, to nie jest jednak stała w innych miejscach. W szczególności, prędkość lotu w punkcie P0 rośnie, a w P1 maleje w tempie zgodnym ze zmienną wartością i znakiem Δ. Mylenie średnich długookresowych i wartości chwilowych w obliczeniach fizycznych zwykle kończy się źle.
Oszacujemy teraz poprawnie wszystkie składowe sił, powołując się na raport komisji MAK o wypadku, oraz znanego rosyjskiego podręcznika dla załóg tupolewów wydanego przez ros. Ministerstwo Transportu, Behtir i in. (1997) "Praktyczna aerodynamika Tupolewa 154". Te źródła pozwolą ustalić siły, które omówiliśmy, i pokazać, że chociaż faktycznie występuje ujemne przyspieszenie w pobliżu punktu P1 (zaś dodatnie koło P0), co nie jest wcale nieoczekiwane, to ma ono zgodną z realiami wartość, parę razy mniejszą niż ta wyliczona z błędnej wartości 13,5 T siły.
SIŁA SUNĄCEGO PO TRAJEKTORII CIĘŻARU: G
Patrząc na raport MAK, ryc. 24,25, 44 i 45, mamy wiele wielkości w punktach P0 (t = 10:39:54) i P1 (t = 10:40:21), z których można obliczyć nachylenie trajektorii. Możemy spojrzeć na nachylenie krzywej wysokości (nad drogą startową) w funkcji czasu, i podzielić je przez prędkość V = 84,4 m/s (zarówno w P0 jak i w P1). Jest to stosunkowo niedokładna metoda, która daje sinus kąta nachylenia trajektorii sin θ = Vz / V = - {0,0415; 0,0760}, odpowiednio w {P0, P1}. Alternatywnie, możemy skorzystać z wykresu wysokości w funkcji odległości od progu pasa. Da to: sin θ = Vz/V = - {0,0366; 0,0677}.
Najdokładniej możemy uzyskać nachylenie trajektorii z chwilowej prędkości pionowej oraz IAS (którą w tym rozdziale z niewielkim błędem przyjmiemy za TAS = V; dokładniejsze wyliczenie daje TAS=1,006 IAS). Prędkość pionową w pobliżu P0 można zmierzyć z danych w linkowanym wyżej raporcie MAK, jako około Vz = -2 m/s, oraz dla P1 Vz = -6 m/s. Standardowa prędkość na ścieżce o nachyleniu θstd = 2o40 ' to (dla prędkości 305 km/h)
Vz,std = V sin θstd = -3,95 m/s ~ -4 m/s.
Tak więc prędkość pionowa była dużo mniejsza niż standardowa szybkość opadania w pierwszym punkcie, ale znacznie większa w drugim. Chwilowe nachylenie trajektorii w P0 i P1 było dlatego bardzo różne, i pomijając poprawkę na mały wówczas wiatr, równało się, odpowiednio: -1,4 ° oraz -4,1 °, zaś
sin θ = Vz / V = - {0,0236; 0,0708}.
Składowa ciężaru W = 80T działająca wzdłuż trajektorii jest równa W sin θ. Była równa: 1,9 T w P0 oraz 5,7 T w P1.
SIŁA CIĄGU: P
MAK podał średnie prędkości obrotowe sprężarki o 65% przy P0 i 34% przy P1. Na podst. rozdziału 2 u Behtira i in. (1997) , możemy przetłumaczyć obroty sprężarki niskociśnieniowej na obroty sprężarki wysokociśnieniowej i odpowiadające nominalne wartości ciągu, używając Tabeli 2 na str. 41 i Rys. 2.1 na str. 39. Rezultatem jest 3 * 57 kN z trzech silników D-30KU-154 w P1 i tylko 12 kN przy biegu jałowym w punkcie P1.
Jednak według Behtira i in. te wartości nominalne wymagają dwóch poprawek. Jedną na to, że silniki zamontowane są obok kadłuba. To i niezerowe kąty dysz względem osi samolotu dają pewna aerodynamiczną interferencję przepływu. Co redukuje siłę ciągu do 94% sumy izolowanych silników. Druga korekta jest większa: wartości w tabeli odnoszą się do silników mierzonych na hamowni, w stanie spoczynku, tj. przy prędkości V = 0. Silnik turboodrzutowy emituje strugę gazów odrzutowych z szybkością około Vst = 400 m/s, a jeśli zostanie umieszczony w zewnętrznym przepływie o tej właśnie prędkości, to nie da żadnej siły napędowej. Siła ciągu poruszającego się silnika jest proporcjonalna do czynnika (Vst - V). Redukcję ciągu odda czynnik korekcyjny (Vst - V)/(Vst - 0) = 1 - V/Vst równy
1 - V / (400 m/s) = 1 - 84,4 / 400 = 0,79.
Łącznie, obie poprawki zmniejszają wartość tabelaryczną aż o 26%, dając po przeliczeniu kN na T siłę ciągu
P = {12,9; 2,7} T w punktach {P0, P1}.
OPÓR AERODYNAMICZNY: D
Charakterystykę aerodynamiczną samolotu TU-154M podsumowano graficznie na ryc. 1.5 na str. 19 podręcznika Behtir et al (1997). Współczynniki siły nośnej i oporu, odpowiednio Cy i Cx, mogą być wyznaczane nawzajem jeden z drugiego lub ze znanego kąta natarcia (AOA). Użyjemy tu najdokładniejszej metody ustalania współczynnika siły nośnej Cy, a następnie graficznie odnajdziemy współczynnik oporu Cx. Współczynnik Cy znajdziemy ze znanego wyrażenia na siłę nośną,
L = Cy (A ρ V2/2)
gdzie A = 180 m2 jest powierzchnią odniesienia skrzydeł (w konfiguracji do lądowania stabilizator poziomy wytwarza stosunkowo niewielki wkład do całkowitej siły nośnej i może być zaniedbany), a ρ = 1,21 kg/m3 to gęstość wilgotnego powietrza w Smoleńsku w dniu wypadku, 300-350 m nad drogą startową. Można to uzasadnić przy użyciu temperatury powierzchni 2° C, standardowego modelu atmosfery i wielokrotnie omawianej gęstości ρ = 1,25 kg/m3 na poziomie pasa startowego. We wzorze V to TAS = true airspeed. Ale ponieważ ciśnienie dynamiczne wskazywane przez szybkościomierz to: (TAS)2 ρ/2 = (IAS)2 ρstd/2, gdzie ρstd = 1.225 kg/m3, to najlepiej używać to IAS i gęstości standardowej.
Uwaga co do wartości A jest taka, że niektórzy biorą powierzchnię całkowitą skrzydła A = 200 m2 zamiast stałej pow. odniesienia 180 m2, i dostają o 10% mniejszą wartość Cy. Można i tak (bo dla L liczy się tylko iloczyn Cy i A), lecz dla nas to nie ma akurat w tym problemie znaczenia (zob. niżej). Współczynnik wymiarowy w nawiasie wynosi 79.6 T. Jest to siła ciśnienia dynamicznego na powierzchnię równą powierzchni odniesienia skrzydła.
Ponieważ siła nośna jest prostopadła do trajektorii, a zatem nachylona tylko o kilka stopni do pionu, siła nośna o bardzo dobrym przybliżeniu może być zapisana jako L = W n, gdzie W = 80T jest ciężarem samolotu, a n (lub nz) jest współczynnikiem obciążenia mierzonym przez akcelerometr i zapisanym w FDR i QAR na pokładzie samolotu (patrz raport MAK). Sens równania natychmiast widzimy w dwóch szczególnych przypadkach: n = 0 i n = 1, gdzie odpowiednio mamy L = 0 i L = W. W punkcie P0 współczynnik obciążenia wynosił n = 0,95, a w punkcie P1 było n = 1,0. Wstawiając L = W n do równania balansu sił, otrzymamy
Cy = (80T) n / (79.6T) = {0.95; 1.0} w punktach {P0, P1}. (Przy konwencji, gdzie A=200 m2 byłoby Cy = {0.84; 0.88}).
Dlaczego zaszła pomiędzy rozważanymi punktami tak mała zmiana współczynnika siły nośnej, 0.95-->1 ? Wynika to z bardzo niewielkiej zmiany kąta natarcia AOA. Nachylenie charakterystyki Cy(AOA) wynosi ~0,1 na 1 stopień zmiany AOA, stąd wnioskujemy o różnicy AOA równej jedynie +0,4 stopnia między punktami P0 i P1. Jest to łatwe do zrozumienia geometrycznie: AOA, oprócz pewnej stałej zależnej od umocowania i skręcenia skrzydła, jest sumą kąta pochylenia kadłuba i indukowanego kąta natarcia spowodowanego przez pionową prędkość opadania samolotu. Widzieliśmy, że indukowany kąt to {1,4; 4,1} stopni w dwóch rozpatrywanych punktach (gdyż jest to kąt nachylenia ścieżki z odwróconym znakiem). Rysunki w raporcie MAK dają zarejestrowane kąty pochylenia: {0, -3} stopni. Dlatego szacowany AOA = const + {0+1,4; -3+4,1} = const + {1,4; 1,1} stopni. Ponownie uzyskujemy bardzo mały wzrost (o -0,3 stopnia) między punktami P0 i P1. AOA uzyskane z przyspieszenia pionowego wzrastają o +0,4 stopnia, podczas gdy AOA uzyskane z kąta pochylenia kadłuba zwiększa się o -0,3 stopnia. Ta niewielka rozbieżność mieści się w błędach pomiarowych wielkości z raportu MAK i zasadniczo ilustruje, że AOA z w dobrym przybliżeniu pozostaje stałe, na tym etapie lotu, gdzie nie było dostatecznie dużych zmian położenia sterów. Tak mówi też mechanika lotu, co potwierdza fizyczną spójność danych z czarnych skrzynek.
Dodatkowym, znanym faktem jest to, że współczynnik oporu w konfiguracji do lądowania jest mało wrażliwy na zmiany w AOA i współczynnik siły nośnej (Rys.1.5 w Behtir et al. 1997; stąd wybór wartości A i konkretna wartość Cy nie są dla Cx istotne). Wobec ustawienia w rozpatrywanej fazie podejścia klap na 36 stopni, poprzez interpolację uzyskaliśmy z naszych wartości Cy następujące wartości współczynnika oporu Cx: Cx = {0,165; 0,17} w punktach P0 i P1. Odpowiednie siły oporu są równe
D = Cx (A ρ V2/2) = {0,165; 0,17} 79.6 T = {13,1; 13,5} T.
SIŁA WYPADKOWA: Δ
Teraz obliczyliśmy już wszystkie siły składające się na siłę netto Δ. Podstawiając wartości w jednostkach T, otrzymujemy
Δ = P +G - D
+1.7 = 12,9 +1,9 -13,1 (przy P0)
-5,1 = 2,7 +5,7 -13,5 (przy P1)
Mimo, że podawaliśmy wartości ułamkowe, łączna dokładność obliczeń jest rzędu ±1,5 T ( ±2% masy samolotu lub ±12% siły oporu). Używając masy samolotu M = 80000 kg przeliczamy siłę wypadkową na przyspieszenie wypadkowe:
aΔ = dV/dt = {+0,021; -0,064} g = [{+0,21; -0,63} ± 0,18] m/s2 .
Tak jak wskazują wykresy V(t) w raporcie MAK, zmiany prędkości są małe w pobliżu P0: dV/dt ~ +0,21 m/s2. Nawet jeśli przyspieszenie aΔ zostanie utrzymane przez 10 sekund, prędkość wzrośnie umiarkowanie, o +2,1 m/s czyli 7.5 km/h; w rzeczywistości nastąpił w pobliżu P0 wzrost V(t) o 5 m/s.
Ale w pobliżu P1, a zwłaszcza zaraz po tym punkcie, zarejestrowana prędkość spada dość szybko. Czy spadek V spowodowany jest siłą wypadkową -5 T którą otrzymaliśmy? Tak, całkiem możliwe! Po 10 sekundach prędkość, zgodnie z powyższymi obliczeniami, powinna spaść o | dV | = 10 * (0,63 ± 0,18) m/s = (6,25 ± 1,8) m/s = (22,5 ± 6,5) km/h. Rzeczywiście, prędkość V, jak widać w raporcie komisji, stopniowo spada o |dVobs| = 17 km/h, z 307 do 290 km / h, w przedziale 10 sekund wokół punktu P1. Zarejestrowane opóźnienie ruchu jest więc zgodne (z dokładnością do 1σ) z wartością aΔ przewidywaną na podstawie siły wypadkowej Δ.
WNIOSKI KOŃCOWE
Rzekomy paradoks wartości sił na podejściu samolotu PLF 101 do Smoleńska nie istnieje. Wszystkie siły i przyspieszenia uzyskane w dwóch charakterystycznych punktach trajektorii, m.in. z charakterystyk aerodynamicznych tupolewa 154M, zgadzają się z historią lotu zarejestrowaną w czarnych skrzynkach i rejestratorach szybkiego dostępu.
Wszystkie wartości sił opublikowane przez niejakiego Niegracza/Qur-cośtam zostały wyliczone błędnie, z kilku powodów wypunktowanych wcześniej w podrozdziale 'Rozwiązanie', głównie przez głębokie niezrozumienie tematyki, wiodące do błędnych założeń, i przez nieuwzględnienie prawdziwej trajektorii samolotu w przestrzeni. Na przykład, w punkcie P0 (P1) siły oporu wynoszą 13,1 (13,5) T, a nie 23 T; składowa ciężaru samolotu wynosi 1,9 (5,7) T, a nie 6,8 T, zaś siła ciągu to 12,9 (2,7) T zamiast 16,5 (3,0) T. Doprowadziło to do błędnego mniemania użytkownika, że w okolicy punktu P1 siła wypadkowa ma wartość "-13,5 T zamiast 0 T", błędnie przewidzianych na podstawie kinematyki ruchu jednostajnego (sic). Prawidłowe obliczenie podane wyżej daje prawie trzykrotnie mniejszą siłę wypadkową -5,1 T ± 1,5 T w drugim rozważanym punkcie, wartość dobrze zgodną z około -3,9 T siły spowalniającej ruch samolotu, która wynika z zarejestrowanej w skrzynkach zależności V(t).
Dzięki fizyce lotu płatowca, została obalona jeszcze jedna teoria spiskowa.
(c) Paweł Artymowicz, 2 marca 2019 r
Podziękowanie: Pan Michał Jaworski przypomniał mi że referencyjna wartość A to 180, nie 200 m2; zmieniłem tekst notki.
Komentarze