Piękna fizyka: słońca, białe karły i czarne dziury

W 19. wieku nie wszyscy wierzyli w realność atomów. W 21. w. trzeba by być członkiem towarzystwa płaskiej ziemi lub podkomisji drugiego sekretarza Partii, by tak ignorować fizykę i fakty. Jednak nadal są ludzie, którzy sądzą, że nie istnieją czarne dziury. Pokażę tu prosto, że istnieją, stąpając po śladach gigantów astrofizyki. Po drodze zrozumiemy co to są białe i brązowe karły.

Ten rozdział pokrywa zakres kilku godzin wykładów astrofizyki dla fizyków. 

ZROZUMIEĆ CIĄG GŁÓWNY

Jak opowiedziałem w ostatnim blogu z serii "Piękna Fizyka", prace Einsteina i Eddingtona zaowocowały poparciem teorii względności obserwacjami astronomicznymi dowodzącymi przewidywanego przez OTW ugięcia promieni światła przez masywne ciała, oraz propozycją zrozumienia skąd nasze słońce bierze energię tak łaskawie dla nas wyświecaną. Innymi słowy: dlaczego gwiazdy świecą. Większość z nich, te które nazywamy gwiazdami ciągu głównego, zamienia wodór w hel, wyświecając różnicę masy produktu i składników zgodnie ze wzorem E = mc².

Empirycznie, na wykresie kolor-wielkość gwiazdowa, lub równoważnym wykresie mocy promieniowania L w funkcji temperatury powierzchni lub typu gwiazdowego (wykresie Hertzsprunga-Russella) widać wyraźnie że ciąg główny usiany jest gwiazdami o mocy promieniowania rosnącej szybko wraz z rosnącą temperaturą powierzchni. Tam za wszystko odpowiada masa gwiazdy M (i w mniejszym stopniu jej skład chemiczny), i za jej promień R i za moc L, i za temperaturę wnętrza T (T~10⁷ K w przypadku słońca) i temperaturę powierzchni T_ef (5780K na słońcu). Eddingtonowi udało się przewidzieć, że moc promieniowania gwiazdy rośnie potęgowo, jak L ~ M³, wraz z masą M. Łatwo to wykazać i robi się to na studiach astronomii, por. np. podręcznik PWN z serii Astrofizyka autorstwa prof. Marcina Kubiaka "Gwiazdy i materia międzygwiazdowa".

Gradient ciśnienia termicznego (lub ciśnienia promieniowania dla gwiazd masywniejszych niż słońce) daje przyspieszenie równoważące przyspieszenie grawitacji -GM(r)/r², które zależy od tego ile masy M(r) znajduje się wewnątrz promienia r (co dla ciał sferycznie symetrycznych udowodnił Newton w "Zasadach matematycznych filozofii przyrody"). Równanie równowagi hydrostatycznej cienkiej warstwy gwiazdy o grubości dr, gęstości ρ i ciśnieniu P(r) mówi, że różnica ciśnień dP na radialnej odległości dr równoważy grawitację; ma zatem postać:

dP = -G M(r) ρ r^-2 dr                                                                                             (1)

Postępując za Eddingtonem nieco brawurowo, podstawmy tu zamiast małego przyrostu dP różnicę ciśnień w środku i na powierzchni gwiazdy (~zero!), za M(r) przyjmijmy pewną stałą razy M, za dr cały promień R, za gęstość średnią gęstość gwiazdy równą M/V = 3M/(4π R³), a zamiast r jakąś "średnią" wartość czyli stałą rzędu jedynki razy R. Otrzymamy oszacowanie (z dokładnością do stałej rzędu jedności) na ciśnienie centralne

P ~ GM²/R⁴

Teraz, używając równania gazu P = ρ kT/m, gdzie k to stała Boltzmanna zaś m to średnia masa cząsteczki w zjonizowanym wnętrzu słońca, mniej więcej równa masie protonu, możemy napisać oszacowanie na T we wnętrzu słońca (to równanie, zwane zależnością wirialną, ma kilka różnych wyprowadzeń, jako że wynika wprost z równowagi energii termicznej cząstki po lewej stronie i grawitacyjnej po prawej):

kT/m ~ GM/R                                                                                                           (2)

W ten sposób już pod koniec 19. wieku oszacowano poprawnie temperaturę wnętrza słońca na T ~ GMm/(kR) ~ 10⁷ K,  10 mln stopni (K lub C). 

A oto jak Eddingtonowi udało się wyjaśnić blisko sto lat temu potęgową zależność mocy gwiazdy ciągu głównego od jej masy. Z równania (2) widzimy, że T ~ M/R. Aby wiedzieć jak L zależy od M, musimy powiązać L z przebiegiem temperatury T w gwieździe. Tę wiedzę daje nam równanie transportu promienistego energii, które można ściśle wyprowadzić, ale odciągnęło by nas to od tematu notki. To równanie mówi, że tam gdzie pochłaniane lub rozpraszane są fotony, tam zmniejsza się gęstość strumienia ich energii. (Na powierzchni gwiazdy strumień energii to moc L podzielona przez powierzchnię gwiazdy 4πR².  Wewnątrz podobnie, tylko mamy mniejsze L i mniejszą powierzchnię 4πr².) Gęstość energii gazu fotonów jest proporcjonalna do czwartej potęgi ich temperatury. [Ten kto lubi całkować, może przecałkować rozkład energii w planckowskim widmie ciała doskonale czarnego po częstotliwości f i się o tym przekonać; wystarczy zmienić zmienną całkowania z f na hf/(kT)]. Temperatura T fotonów spada dokładnie w tym samym tempie, co temperatura gazu cząstek materialnych, bo gwiazda jest w dokładnej równowadze termicznej, gdzie zbiory jonów, elektronów i fotonów mają lokalnie tę samą wartość T, będącą miarą średniej energii cząsteczki gazu. Równanie na spadek energii radiacyjnej mówi, że zależy on od strumienia energii i od stopnia nieprzezroczystości materii

const * d(T⁴)/dr = -κ ρ (L/4πr²)

Po obu stronach tego wyrażenia stoi część strumienia energii usunięta w warstwie dr, podzielona przed wartość dr, w granicy małego przyrostu dr. Współczynnik nieprzezroczystości lub inaczej ekstynkcji κ oddaje tu zdolność do usuwania energii ze strumienia fotonów prącego od centrum na zewnątrz gwiazdy. Dokładniej mówiąc,  w każdej warstwie gazu o grubości dr jest duża liczba centrów rozpraszania fotonów, która jest proporcjonalna do n = liczbowej gęstości objętościowej tj. liczby tych centrów na metr sześcienny. Są to głównie swobodne elektrony z których każdy działa na fotony jak tarcza o polu powierzchni równym przekrojowi czynnemu Thomsona σ_T  = 66.5 fm². Eddington założył, że współczynnik masowy ekstynkcji (pochłaniania + rozpraszania) w gwieździe, κ = σ_T/m, jest stały. Upraszczając równanie różniczkowe transportu promieniowania (dT⁴ --> T⁴, r --> const*R, ρ --> ~M/R³), dostaniemy wziąwszy pod uwagę równanie (2) następującą proporcjonalność:

(M/R)⁴(1/R) ~ (M/R³) (L/R²)

lub po uproszczeniu

L ~ M³                                                                                                                     (3)

Ta reguła jest w przybliżeniu spełniona przez gwiazdy podobne do naszej, chociaż empirycznie wyznaczony wykładnik zależy troszkę od zakresu masy M, o którym jest mowa. Popatrzmy na ten wykres: pomiędzy masą 0.1 a 10 mas słońca (różne o czynnik 10²) moc promieniowania rośnie (ciągnąc prostą linię na wykresie podwójnie logarytmicznym) o czynnik 10⁷, stąd średnio mamy L ~ M^3.5 z obserwacji.

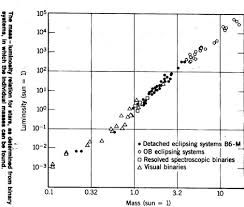
Przybliżona zgodność z obserwacjami to wielkie osiągnięcie teorii budowy wewnętrznej gwiazd sprzed prawie stu lat. Z zależności L(M) dowiadujemy się, że czas "palenia" wodoru na ciągu głównym, który  jest proporcjonalny jest do masy gwiazdy (razy c²) podzielonej przez moc L, jest odwrotnie proporcjonalny do kwadratu masy gwiazdy (lub nawet większej potęgi, empirycznie). Bardzo masywne gwiazdy żyją tylko 10⁷ lat, słońce 10 mld lat, a mniej masywne gwiazdy tak długo, że żadna jeszcze nie umarła, czyli nie zeszła z ciągu głównego, od czasu wielkiego wybuchu.

DZIWNY TOWARZYSZ SYRIUSZA

Syriusz  -- alfa Canis Majoris, α CMa, to bardzo jasna gwiazda (minus pierwszej wielkości, dwukrotnie masywniejsza od słońca) położona "na dół i w lewo" od widocznego w tej porze roku na południu Oriona. Leży w gwiazdozbiorze wielkiego psa, gdyż Syriusz był psem Oriona w mitologii Greków.  (Σείριος znaczy ognisty).  Jest tak ważną gwiazdą, że aż ma polską stronę sieciową w wikipedii. (Dla kontrastu, nie uznajemy jak widać ważności żadnych innych linkowanych dotąd pojęć, gdyż nie znalazłem ich stron polskojęzycznych, a tylko w językach sąsiadów). Pod koniec życia, matematyk i astronom niemiecki Fryderyk Bessel w r. 1844 odkrył obserwując kształtu tor ruchu gwiazdy na niebie, że Syriusz jest gwiazdą podwójną: Syriuszowi A o masie 2.1 mas słońca towarzyszy, okrążając go co 50 lat, niewidoczny w momencie odkrycia Syriusz B, o masie mniej więcej równej słonecznej. (Bessel nie tylko zdefiniował ważne funkcje Bessela, ale też prowadził tak dokładne pomiary pozycyjne gwiazd, że odkrył przewidywane dużo wcześniej przez teorię Kopernika zjawisko paralaksy, a przez to wyznaczył jako pierwszy odległość do pobliskiej gwiazdy 61 Cyg).  Dlaczego jednak α CMa B jest obiektem tak słabym, tak trudno widocznym, że zauważono go dopiero 18 lat później jako gwiazdę o mocy L dziesięć tysięcy razy mniejszej niż  α CMa A? Od odpowiedzi na to pytanie zaczęła się pełna przygód historia badan dziwnych gwiazd w naszej i w innych galaktykach.

Początkowo zaproponowano, że gwiazda ta jest tak ciemna, bo ma odpowiednio małą temperaturę powierzchni T_ef. Mamy bowiem L = (4 π R²) (σ T_ef⁴)  = powierzchnia  * strumień promieniowania (prawo Stefana-Boltzmanna z ich stałą σ). Przy użyciu największego wtedy na świecie, 100-calowego teleskopu Hookera w obserwatorium Mount Wilson niedaleko Los Angeles, Walterowi Adamsowi udało się dopiero w 1914 r. wykazać spektroskopowo, że to nie temperatura, a powierzchnia gwiazdy jest bardzo mała. Temperatura natomiast jest, wręcz przeciwnie, mniej więcej tak wysoka jak głównego składnika układu. Wynik był jednak szokujący na tyle, że nie wszyscy astronomowie w niego uwierzyli: Syriusz B miał być wielkości Ziemi, która ma sto razy mniejszy niż słońce promień! A jego gęstość miała być zatem 100³ czyli milion razy większa niż słońca. O tym, że jest to prawda przekonał Adams wszystkich dziesięć lat później, w 1924 r., posługując się przewidzianym liczbowo przez Karla Schwarzschilda w 1915 r. efektem fizycznym wynikającym z OTW Einsteina: przesunięciem ku czerwieni światła wydostającego się z pobliża masywnego ciała. Foton wyświecany przez atomy z daną częstotliwością (i proporcjonalną energią) na powierzchni białego karła (jak nazwano obiekty typu Syriusza B), traci energię i spada jego częstotliwość, kiedy wydostaje się ze studni potencjału grawitacyjnego do nieskończoności. Dokładniej, częstotliwość spada o czynnik równy 1 - R_Sch/R, gdzie R to promień gwiazdy, a R_Sch to promień Schwarzschilda

R_Sch = 2GM/c²                                                                                                               (3b)

Ta wielkość to nic innego jak promień horyzontu zdarzeń nierotującej czarnej dziury. Liczbowo mamy 

R_Sch = 3 km (M/M_sun)  << R (białego karła)

Grawitacyjne przesunięcie ku czerwieni było więc nieduże (procentowo takie jak 3 km w porównaniu z promieniem Ziemi). Ale obserwowalne. I to potwierdziło jeszcze raz, astrofizycznie, ogólną teorię względności. Zauważmy tu jednak, że przesunięcie grawitacyjne może być duże. Kiedy? W krańcowym przypadku wtedy, kiedy uczyni częstotliwość fotonu zerem a jego długość fali nieskończonością, czyli wtedy, gdy foton wysłany jest z powierzchni oddalonej od masy M o promień Schwarzschilda, lub inaczej promień czarnej dziury. Wszystko się zgadza. Nawet światło ma wielkie trudności, by wydostać się z tak małej odległości, a z wnętrza czarnej dziury nie wydostaje się nic, ani cząstki ani fale (promieniowanie Hawkinga nie pochodzi z wnętrza, a z okolicy horyzontu dziury). 

Syriusz A w środku, wraz ze swym dziwnym towarzyszem, białym karlem Syriuszem B, o podobnej temperaturze, dwa razy mniejszej masie i dziesięć tysięcy razy mniejszej jasności (Kropka poniżej i w lewo, na fotografii z teleskopu kosmicznego Hubble'a).

POCZĄTKI FIZYKI MATERII ZDEGENEROWANEJ

Jest rok 1928. Do Madras (obecnie Chennai) przybywa z wykładem Arnold Sommerfeld. Osiemnastoletni student tamilski, bratanek fizyka i noblisty C.V. Ramana, Subramanyan Chandrasekhar, odbywa z nim w hotelu inspirującą rozmowę. Sommerfeld daje studentowi preprint swej pracy o teorii elektronów swobodnych w metalach, gdzie stosuje do gazu elektronowego teorię statystyki kwantowej. Praca jest po niemiecku, jak większość poważnych artykułów naukowych na początku 20. wieku, ale to nie problem, bo Chandra zna niemiecki. Zapoznaje się z nową statystyką Fermiego-Diraca, opisującą niespołeczne zachowanie cząstek o spinie połówkowym (fermionów): za wszelką cenę nie chcą być w takim samym stanie kwantowym, jak sąsiedzi. To reguła Wolfganga Pauliego. Poznaje też zasady budowy wewnętrznej gwiazd opisane przez Artura Eddingtona w książce The Internal Constitution of Stars, i dowiaduje się o białych karłach i idei Ralpha Fowlera, że utrzymywane są w równowadze przez kwantowomechaniczne ciśnienie materii fermionowej. Gdy Chandra dostaje stypedium indyjskie i zaproszenie od Fowlera do koledżu Newtona (Trinity) w Cambridge, UK, wsiada na statek parowy w porcie w Bombaju (obecnie Mumbai) w lecie 1930 r. Podróż będzie długa, ale Chandra nie będzie się nudził. Połączy teorię kwantową gazu elektronowego z teorią budowy wewnętrznej białych karłów i pokaże jak zależy promień takich gwiazd od masy. Obliczy, że promień zmniejsza się z masą, a gdy ta osiąga krytyczną wartość (masę Chandrasekhara ok. 1,4 masy słońca), gwiazda kurczy się pod wpływem grawitacji do punktu, do postaci czarnej dziury. Eddington nie przyjmie tego wniosku i parę lat później sarkastycznie wypowie się bardzo publicznie o pracy swego asystenta w 1935 r., tak dotkliwie że ten postanowi zaprzestać badań nad wnętrzami gwiazd i przeprowadzić do Ameryki, by zająć się innymi działami astrofizyki teoretycznej, z wielkim zresztą powodzeniem. Pół wieku pózniej, w 1983 r., za badania rozpoczęte na statku z Bombaju do Dover, otrzyma nagrodę Nobla z fizyki.

POWTÓRZMY OBLICZENIA ZE STATKU

Pokażę jaka jest zależność promienia od masy białego karła i dlaczego te obiekty są sto razy mniejsze od gwiazd i milion razy gęstsze. Do tego potrzeba wiedzieć 'tylko' jedną rzecz, jak ciśnienie materii zdegenerowanej  zależy od jej gęstości (zdegenerowanej = tak gęstej, że ciśnienie to bierze się z kwantowej zasady W. Pauliego, a nie np. z ruchów termicznych cząsteczek materii w próżni). Temperatura nie wchodzi w tę zależność, nie jest ważna i w odróżnieniu od materii normalnej, niezdegenerowanej, nie kontroluje ciśnienia. Można by nawet przyjąć że równa jest zeru absolutnemu, a i tak ciśnienie gazu elektronów w gęstej gwieździe będzie w stanie zrównoważyć siłę grawitacji większą dziesięć tysięcy razy niż w słońcu.

Wszystkie cząstki podlegają prawu nieoznaczoności Wernera Heisenberga:  nieoznaczoność pędu razy rozmycie pozycji mają wielkość co najmniej ok. stałej Plancka h: Δp  Δx > ~ h.  Rozważmy pudełko sześcienne o boku L i objętości V w którym trzymamy N cząstek, dajmy na to elektronów (jak się okaże, rozmiar pudełka nie gra roli dla równania stanu gazu zdegenerowanego, którego szukamy). W tym pudełku mechanika kwantowa przewiduje skwantowane stany o długościach funkcji falowej takich, że liczba połówek fali jest całkowita, podobnie jak pęd w każdym z 3 kierunków w przestrzeni jest wtedy całkowitą wielokrotnością (h/L). Dla fizyka, pęd jest wektorem w 3-wymiarowej przestrzeni pędów, przestrzeni która jest skwantowana i składa się z komórek elementarnych o objętości (h/L)³. W każdej komórce przestrzeni pędów może znajdować się tylko jeden elektron o danym stanie kwantowym, a zatem w sumie dwa, różniące się kierunkiem spinu. Gdy zapełniamy nasze pudełko elektronami, idzie nam to coraz ciężej. Musimy nadawać elektronom coraz wyższy pęd, aby zechciały wejść do pudełka. Z początku bowiem mają wszystkie małą energię kinetyczną i pęd, ale po zajęciu komórek w pobliżu zera pędu w każdym kierunku, mogą jedynie być umieszczone w bardziej odległych, pustych jeszcze komórkach, o większej długości wektora pędu. Ostatni, N-ty elektron znajduje miejsce na powierzchni sfery o promieniu Fermiego p_F. Całe wnętrze sfery Fermiego jest wypełnione równomiernie przez elektrony. Nie ma pustostanów, gdyż starając się osiągnąć stan najmniejszej energii przepychają się bezskutecznie ku początkowi układu współrzędnych (p_x,p_y,p_z). Objętość sfery Fermiego podzielona przez objętość komórki elementarnej daje połowę liczby elektronów: N/2 = (4π/3) p_F³ (L/h)³, a uwzględniając, że gęstość objętościowa (liczba elektronów na m³) to n = N/V = N/L³, mamy:

n = 2 (4π/3) p_F³  h^-3                                                                                             (4)

Zatrzymam się tu by pokazać, że w każdym rodzaju gazu, czy to gazu cząstek czy fotonów, ciśnienie gazu na ścianki naczynia (pudełka o boku L ) równe jest 2/3 (1/3) energii cząstek gazu przypadającej na jednostkę objętości, w przypadku nierelatywistycznym (ultrarelatywistycznym).  Mamy dwa skrajne przypadki: pierwszy nierelatywistyczny, kiedy prędkości elektronów nie są porównywalne z prędkością światła c, a energia kin. wyraża się wzorem E = p²/2m = mv²/2. Drugi, ultrarelatywistyczny, kiedy to energia przekracza znacznie energię spoczynkową cząstek, E>>mc², asymptotycznie zbliżając się do E = pc.

Ustalmy,  o ciśnieniu na którą konkretnie ściankę będziemy mówić: niech będzie to jedna ze ścian prostopadłych do osi x. Rozważmy najpierw jedną cząstkę o składowej pędu p_x i składowej prędkości v_x, odbjającą się regularnie i bez strat energii od ścian pudełka. Zderzenia elastyczne z rozważaną ścianką następują co dt=2L/v_x sekund, każdorazowo przekazując jej pęd dp_x=2p_x. Tempo przekazu pędu do ścianki, czyli siła F_x=dp_x/dt = p_x v_x /L, rozkłada się w przypadku N takich cząstek na pole ścianki L² i daje ciśnienie

P = < p_xv_x> N/L³ = < p_xv_x> n.                                                                                     (5)

Znaki uśredniania pokazują, że powinniśmy uśredniać po cząstkach mających różne wartości pędu i prędkości. Przy tym, wszystkie 3 kierunki (x,y,z) są równouprawnione, dlatego możemy napisać 

< p v > = < p * v > = < p_xv_x >  +  < p_yv_y >  +  < p_zv_z> = 3 < p_xv_x>,

gdzie p i v to wektory skierowane zawsze w te samą stronę a * to iloczyn skalarny. Podstawiając do wzoru (5), otrzymujemy całkowicie ogólny wzór stosujący się do wszelkich możliwych gazów:

P = (n/3)  < p v >                                                                                                          (6)                                                        

Dla przykładu, nierelatywistyczny i niezdegenerowany (rzadki) gaz taki jak plazma wewnątrz słońca ma cząsteczki, których p = mv, oraz ciśnienie P = (2/3) n < p²/2m > = (2/3) (ρ/m) < mv²/2 >. Innymi słowy, ciśnienie jest równe 2/3 energii kinetycznej cząstek, N < mv²/2>, podzielonej przez objętość V, czyli 2/3 gęstości energii termicznej.  

Średnia energia kinetyczna cząsteczki = < mv²/2 > = (3/2) kT, gdyż  kT/2  to po prostu inna nazwa na energię średnią ruchu w każdym z 3 kierunków: temperatura i energia to dwa określenia na to samo, z dokładnością do stałej. W ten sposób wyprowadziliśmy mikroskopowo słynne równanie stanu gazu doskonałego (równanie Clapeyrona, ogólniejsze niż prawo Mariotta czy Boyle'a):

P = n kT =  ρ kT/m.         (albo: PV = NkT, gdzie V to objętość gazu)                   (7)

A co będzie, gdy cząstki poruszają się relatywistycznie, z prędkością praktycznie równą c? Wtedy < p v > = < pc > = < E > i znów dostajemy ciśnienie proporcjonalne do energii kinetycznej (spoczynkowa jest wtedy znikomo mała i E=E_kin). Tyle, że z mniejszym współczynnikiem liczbowym: zamiast 2/3 mamy 1/3 gęstości przestrzennej energii:

(ultrarel.)  P =   (n/3) < E >.

Ta zależność opisuje tak samo dobrze gaz fotonów jak i gaz degenerowany elektronów w białym karle lub Jowiszu (tak, Jowisz też jest wielką kwantową cząstką!). Tu można przypomnieć, że prawo promieniowania Maxa Plancka prowadzi do wniosku, że gęstość promieniowania to aT⁴, zaś ciśnienie promieniowania to aT⁴/3, więc wszystko się zgadza; ciśnienie to 1/3 gęstości energii relatywistycznych zawsze fotonów.

Wroćmy na koniec do naszego gazu zdegenerowanego (z ciśnieniem kwantowo-mechanicznym). Jeśli cząstki mają prędkości nierelatywistyczne, jak w białym karle Syriuszu B, to mamy v = p/m. Wówczas

P = (1/3) (n/m) < p² > =(1/5) (n/m) p_F²                                                    (8)

W ostatnim równaniu skorzystaliśmy z tego, że średnia wielkości p² w sferze o promieniu p_F jest równa (3/5) p_F². 

To łatwo pokazać całkując od zera do p_F: < p²> = ∫   p² (4π p²) dp / ∫ (4π p²)  dp  = (p_F⁵/5)/(p_F³/3) = 3/5 p_F².

A DLACZEGO NIE PROTONY?

Dlaczego Fowler i Chandra twierdzili, że to właśnie elektrony, a nie protony lub jądra helu dostarczają ciśnienia kwantowego? To wynika z równania (8) i tego, że np. w plazmie wodorowej, gęstość objętościowa n jest dla protonów i elektronów taka sama, podczas gdy masa m cząstek różnią się o czynnik prawie 2000, preferując szybsze elektrony o mniejszej masie m w mianowniku wyrażenia na P. Elektrony mają taki sam przekaz pędu w zderzeniu ze ścianką pudełka, ale prawie 2000 razy większą częstość zderzeń i proporcjonalnie większą siłę nacisku na ściany pudełka. Wewnątrz białego karla protony i cząstki alfa nie przepracowują się. [Dominacja elektronów znika natomiast w przypadku ultrarelatywistycznym, gdzie działa ograniczenie prędkości do v=c. Tam i pędy i prędkości są podobne, dlatego wszystkie rodzaje cząstek wnoszą podobny wkład do ciśnienia i muszą być brane pod uwagę; jak widzieliśmy powyżej w równaniu (7), wyrażenie na ciśnienie nie zawiera wzmianki o m, gdyż jest to nie ważna w świecie ultrarelatywistycznym (lub dokładnie zerowa u fotonu) masa spoczynkowa.]

CIŚNIENIE KWANTOWE

Podstawiając p_F² = h² [n /2/ (4π/3)]^2/3 z równania (4) do (8), dostajemy ciśnienie nierelatywistycznego gazu zdegenerowanych elektronów w postaci równania politropy o wykładniku γ=5/3,  P_e ~ n^5/3

P_e=  (h²/5m_e) (8π/3)^-2/3   n^5/3                                                                     (9)

Ultrarelatywistyczne równanie stanu gazu sprowadza się natomiast do innego równania o postaci politropowej z wykladnikiem γ = 4/3:

P = (n/3) < pc > = (nc/4) p_F =   (hc/4) (8π/3)^-1/3 n^4/3 ,                              (10)

ponieważ < p > = ∫ p (4π p²) dp / ∫ (4π p²) dp  = (p_F⁴/4)/(p_F³/3) = (3/4) p_F. Gdy gaz staje się relatywistyczny, jego równanie stanu staje się bardziej miękkie, w tym sensie, że dany stopień kompresji wytwarza mniejszy przyrost ciśnienia. A to, jak za chwilę zobaczymy, nie pomaga stabilności obiektu.

PROMIEŃ W ZALEŻNOŚCI OD MASY

Przypomnijmy sobie na koniec równanie równowagi statycznej (1) i jego uproszczenie:

P/R  ~ ρ M/R²

Podstawiając P ~ ρ^γ, oraz ρ ~ M/R³, otrzymujemy zależność

R  ~ M^{(γ-2)/(3γ-4)}                                                                                             (11)

Rozważmy następujące przypadki opisujące coraz masywniejsze ciała: 

1. Nierelatywistyczny materiał niemal nieściśliwy, np. skały w nieporowatej planetoidzie: γ >>> 1, gdyż nawet b. małe zmiany objętości i gęstości owocują wielkimi zmianami ciśnienia.

R ~ M^1/3.

Odwracając zależność, M ~ R³, co oczywiście jest prawdą w ciałach nieściśliwych. Ale gdy zbierzemy w jednym miejscu dostatecznie dużo skał a nawet gazu głównie wodorowo-helowego, grawitacja ugniata je w ciało coraz bardziej ściśliwe. Jowisz jest gazowy, a ma gęstość centralną podobną do gęstości Ziemi.

2. Nierelatywistyczny gaz zdegenerowany w chłodnym ciele o rząd wielkości masywniejszym niż Jowisz.. Duża masa takiego super-Jowisza kompresuje chłodne wnętrze do gęstości, gdzie pojawiają się efekty kwantowej zasady wykluczania Pauliego. To zmniejsza γ do mniej więcej γ ~ 2. Wtedy promień przestaje zależeć od masy i osiąga maksymalną wartość. Dzieję się tak we wnętrzu brązowego karła,

 R ~ M⁰ = const.

Oznacza to, że nigdzie nie ma ciał (nie produkujących energii w przemianach jądrowych, tj. ciał 'chłodnych') takich jak planety, brązowe karły i stygnące białe karły, o promieniu znacznie przekraczającym promień Jowisza. To jedno z największych chłodnych ciał  we wszechświecie (z dokładnością do czynnika 2)!

3. Trzeci przykład to zdegenerowany, nierelatywistyczny gaz we wnętrzu białego karła, pozostałości po ewolucji gwiazdy typu słońca lub nieco masywniejszej, gdzie γ=5/3=1.666.

R ~ M^-1/3

Chandra wyprowadził ów ciekawy wynik: promień białego karła zmniejsza się z masą jak pierwiastek sześcienny z masy. Ciekawa jest też wartość liczbowa, którą można uzyskać z równania (9) nie pomijającego stałych fizycznych i matematycznych. Promień Syriusza B powinien wynosić około 10000 km, tj. być porównywalny z promieniem Ziemi. W istocie, Syriusz B ma mniej więcej rozmiar Ziemi, która ma promień 6370 km.  Dopiero przy tak małym promieniu osiągnięte zostają gęstości przy których ciśnienie degeneracji materii przybiera dominujące znaczenie.

4. Zmierzamy teraz ostrożnie do granicy γ = 4/3, gdzie coś dziwnego dzieje się z wykładnikiem zależności R(M). Przeczuwając kłopoty, bierzemy P ~ ρ^γ, gdzie  γ = 4/3 + ε,  a ε ma małą wartość 0 < ε << 1. 

R  ~ M^-2/(9ε)
Jak widać, przy malejących epsilonach dostajemy bardzo duży ujemny wykładnik i wniosek, że spadek R z masą następuje bardzo szybko. W końcu,  gdy osiągamy wartość γ=4/3=1.333, promień gwiazdy spada do wartości zero. Gwiazda kurczy się do czarnej dziury o promieniu mniejszym niż promień Schwarzschilda. To słynny wynik S. Chandrasekhara. Utrata stabilności hydrostatycznej następuje przy wartości masy Chandrasekhara, zależnej nieco od składu chemicznego gwiazdy. Dla składu słonecznego,

M_Ch ~ 1.4 M_sun

I rzeczywiście, nie ma białych karłów o masie przekraczającej ten limit:

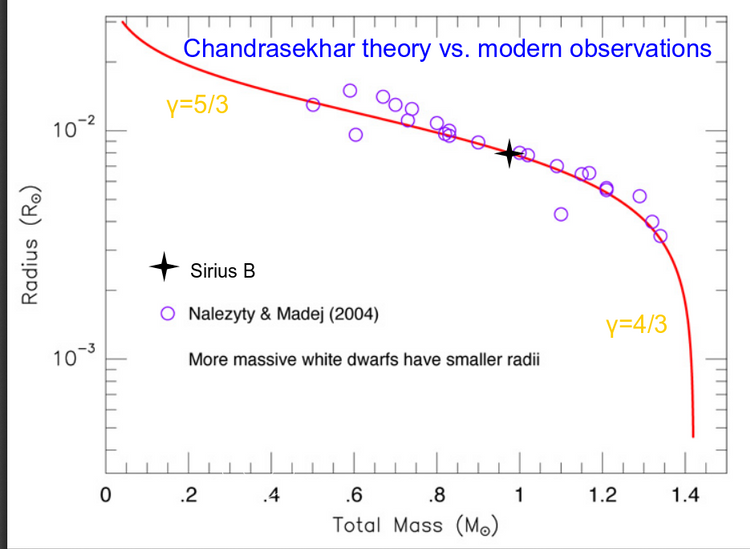
Gdy biały karzeł jest przeewoluowanym składnikiem układu podwójnego gwiazd, a jego towarzyszka jest jeszcze gwiazdą kończącą ewolucję w stadium czerwonego olbrzyma, biały karzeł otrzymuje na ogół poprzez dysk akrecyjny strumień gazu z sąsiedniej gwiazdy. Stopniowo rośnie jego masa, osiągając 1.3 do 1.4 mas słońca

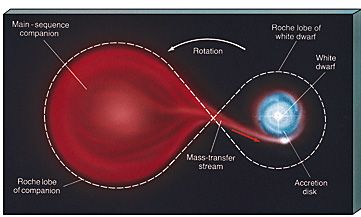
. W sposób nieunikniony kurczy się zapadając w swą jamę potencjału grawitacyjnego, co przyspiesza cząstki w jego wnętrzu do prędkości relatywistycznych. Wykładnik adiabatyczny spada w kierunku γ=4/3 i następuję implozja, kolaps trwający zaledwie ułamek sekundy. Białe karły mają wiele użytecznego dla syntezy jądrowej w wysokich temperaturach materiału, głównie węgla i tlenu, którego gwiazda nie potrafiła przetworzyć na cieższe pierwiastki (takie jak nikiel i żelazo) we wcześniejszych etapach ewolucji. Teraz w warunkach wyzwalania energii grawitacyjnej materia ta nadaje się do szybkiego 'spalenia' -- detonacji. Fala bardzo wysokiej temperatury (miliardy K) przechodzi przez kurczącego sią karła i wybuch termojądrowy rozsadza gwiazdę, po której nie zostaje gwiazda neutronowa ani czarna dziura (przynajmniej tak sądzimy zakładając symetrię wybuchu). Dzięki obserwacji takich odległych supernowych typu Ia, podobnych do siebie bo pochodzących z obiektow o masie bliskiej limitowi Chandrasekhara, a więc nadających się na markery o znanej mocy, odkryto osiemnaście lat temu coś naprawdę nieoczekiwanego. Wszechświat rozszerza się od jakichś 4 miliardów lat nie coraz wolniej, co jest intuicyjnie jasnym przewidywaniem,  gdy chodzi o świat poddany przyciągającej sile grawitacji, a coraz szybciej! Działa więc --nazwijmy to-- antygrawitacja, nazywana ciemną energią lub Lambdą. Dlaczego próżnia zwiększając objętość uzyskuje energię, tego jeszcze za dobrze nie wiemy.

W przypadku zapadania się jąder masywnych gwiazd (ponad 15...20 mas słońca) skomplikowane procesy jądrowe z początku zamieniają energię grawitacyjną na energię neutrin uciekających niepostrzeżenie z wnętrza zapadającego się rdzenia gwiazdy. W końcu jednak gęstość staje się tak fantastycznie duża, że nawet bardzo słabo oddziałujące z materią neutrina nie mogą uciec i grzęzną wśród neutronów (protony i elektrony zamieniane są endotermicznie w neutrony i neutrina) i innych cząstek elementarnych, niektórych dość egzotycznych i krótkożyciowych. Odcięta zostaje droga ucieczki promieniowania neutrinowego; wykładnik adiabatyczny wraca do wartości większych niż 4/3. Implozja przechodzi w eksplozję, a część kuli ognistej materii ucieka w przestrzeń. Reszta zapada się z powrotem tworząc gwiazdę neutronową, bądź czarną dziurę tym bardziej masywną im bardziej masywne było jądro gwiazdy. Tak powstają czarne dziury o masie do kilkudziesięciu mas słońca. Niektóre supernowe typu II, w których giną masywne gwiazdy, w pierwszych dniach wybuchu przekraczają jasnością galaktykę, w której zachodzą. 

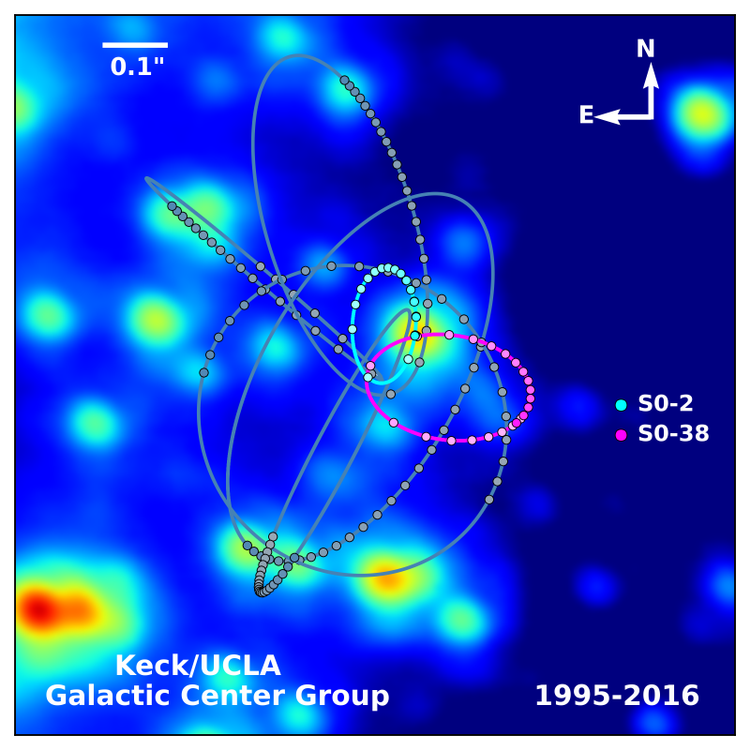
Czarne dziury o masie od paru do kilkudziesięciu słonecznych znalezione zostały w wielu układach podwójnych naszej galaktyki. Kiedy krążą dość blisko sąsiedniego obiektu, zaburzają znacznie otaczającą czasoprzestrzeń wysyłając tzw. fale grawitacyjne. Te zaburzenia czasu i przestrzeni podróżują z prędkością światła. Zostały niedawno odkryte przez niesłychanie czułe eksperymenty (LIGO), jednocześnie  w kilku miejscach na Ziemi. Dwie czarne dziury które mogły wcześniej powstać w supernowych typu II, zlały się w jedną w bardzo odległej galaktyce. To nie tylko potwierdziło teorię względności Einsteina (któryś już raz), ale otworzyło nowy dział astronomii fal grawitacyjnych.  Napisałem o tym więcej tutaj, zaraz po tym przełomowym odkryciu. https://pawelartymowicz.natemat.pl/171221,uklady-podwojne-i-fale-grawitacyjne . Masywne czarne dziury (ponad 10⁴ mas słońca) odkryto w większości zbadanych jąder galaktyk, wiadomo że ich masy są skorelowane z masą centrum galaktyki. Nasza Droga Mleczna ma czarną dziurę o masie prawie 4 milionów mas słońca, co widać jak na dłoni z trajektorii i okresu obiegu obiektów gwiazdowych krążących wokół niej.

Za wiele z opisanych odkryć przyznano nagrody Nobla. Dostali ją jak wiemy Chandra i Einstein (choć nie za teorię względności, bo niektórzy fizycy nie rozumieli jej jeszcze i powątpiewali), również Heisenberg i Pauli.  Dostali je odkrywcy przyspieszającej ekspansji wszechświata, a także odkrywcy fal grawitacyjnych w latach 90tych i parę lat temu. Nie dostali jej natomiast Schwarzschild ani Eddington. Nie otrzymała jej także doktorantka, która odkryła w latach 60tych pulsary - rotujące szybko gwiazdy neutronowe także składające się z materii zdegenerowanej i mające tak jak białe karły swoją własną masę krytyczną zwaną masą Tolmana-Oppenheimera-Volkoffa, mimo że pierwszy wyznaczył ją Lew Landau... ale to opowieść na inny rozdział bloga.