50. Nowe drzewa i skrzydła, matactwa te same

Pokażę, że drzewa nie są ścinane (miażdżone) tylko umiarkowanie wgniatane przez skrzydła i zaraz po tym łamane przez niezbyt szybko lecące samoloty, a do zniszczenia skrzydła tupolewa PLF 101 wystarczyłaby nawet sporo mniejsza 25-centymetrowa brzoza smoleńska, podczas gdy Mig-29 mający w skrzydłach dwukrotnie grubsze blachy niż TU-154, nie traci ich w potyczce z tej grubości sosnami ani brzozami. Potwierdza się więc empiryczna obserwacja, że ~30 cm średnicy drzewa jest przybliżoną linią demarkacyjną między zachowaniem a odpadnięciem skrzydła w zderzeniu z większością gatunków drzew i większością skrzydeł.

Temat dziś bardzo aktualny (Trzech Króli w Betlejem) już dawno w salonie24 omówiłem [1],  więc opowiem o innego rodzaju religii, a dokładniej herezji dotyczącej drzew i skrzydeł.

    MANIPULACJE POLITYCZNE

Minister obrony narodowej Macierewicz zlecił niedawno swym podekspertom z podkomisji smoleńskiej umieszczenie ilustracji z katastrofy samolotu Mig-29 (numer boczny 67 blue) pod Mińskiem Mazowieckim w ich wspólnym, wiekopomnym dziele, ostatnim już najprawdopodobniej wydaniu Białej Księgi Nonsensów o katastrofie z dnia 10.04.10. Publikację przewiduje się na ostatnią już hucznie obchodzoną rocznicę tragicznej katastrofy,  w której poległ najlepszy prezydent Lech Kaczyński oraz zginęło 95 osób, którym postawi się mniejszy pomnik. W księdze pisanej przez dyletantów lotniczych pod dyktando magistra-iberysty, znawcy kultury indian, będzie napisane, że wypadki tupolewa PLF 101 i Miga-29 są ściśle powiązane: ten drugi, w którym wg ministra nic większego się od myśliwca nie oderwało, mimo lądowania awaryjnego z wycinką przesieki w lesie, udowadnia, że ten pierwszy w ogóle nie zaszedł!  Bo w Smoleńsku nie było wypadku, tylko wiadomo co. Świadkowie przeczą ministrowi, mówią że poodrywało się [2]. Widać też jak na dłoni, że wbrew pseudo-inżynierii Szuladzińskiego, są odłamki bez wybuchów. A Macierewicz znów, jak zobaczymy, tradycyjnie pseudonaukowo kłamie i manipuluje, co robił wraz z założoną przez siebie sektą od wielu lat. Pisowska fizyka smoleńska znów przegrała. OK, postaram się nie robić dalszych komentarzy o pseudonauce i polityce. Dalej głównie fizyka stosowana (inżynieria).

    SYMETRIA

Istnieje spora symetria pomiędzy Mińskiem Mazowieckim a Smoleńskiem. Rosjanie mieli bardzo długo garnizon wojsk w Nowom Minskie (gdzie dowodził 'fiński Piłsudski', późniejszy marszałek C. G. Mannerheim, nie znający polskiego [3], słaby w j. fińskim, lepszy nieco w rosyjskim, a z domu mówiący po szwedzku). Polacy mieli jeszcze dłużej garnizon w Smoleńsku, zdobytym m.in. przez szwedzko-polskiego Zygmunta III Wazę. Jednak ta symetria nie rozciąga się na mechanikę dwóch zaistniałych tam wypadków lotniczych, czego powodem były po części różnice między skrzydłami, ale głównie różne średnice pni drzew.

     JAK MOCNY JEST TUPOLEW

Wystarczająco mocny, by latać w silnej turbulencji. Nie dość mocny, by skutecznie atakować skrzydłami niewielkie obiekty naziemne o masie większej niż duży ptak, ponad 10 kg. Proponuję przyjrzeć się uważnie temu tupolewowi TU-154:

To ten, który rok temu rozbił się w Soczi. Nie wzniósł się prawidłowo i zahaczył ogonem (dawniejsza wersja mówi, że skrzydłem) o wodę 50 sekund po starcie. W każdym razie nie dziobem, czyli z małą prędkością. Wybitny iberysta, jego kolega znawca maszyn kopalnianych prof. Witakowski, inż. Dąbrowski od domków jednorodzinnych i reszta tej wesołej kompanii powtarzają od lat w kółko, że tupolew spadający w las łatwo go zetnie i odleci. Jeszcze bardziej zadziwiają wyniki wieloletnich badań teoretycznych prof. Biniendy z miejscowości Akron. Samolot pasażerski TU-154M w przypadku gdy spada na ziemię jak w Smoleńsku... nie rozpada się. Na przykład, po zrobieniu półbeczki orze ziemię statecznikiem i tym statecznikiem amortyzowany, ląduje w całości nie zabijając nikogo. Naprawdę nie żartuję, proszę sprawdzić. Zgodnie z wiarą w "miękką" ziemię w Smoleńsku (która miała zrodzić wg wynalazcy urządzenia do usuwania piegów Joergensena wielki krater), lądując z małą prędkością w dużo bardziej "miękkiej" wodzie TU-154 nie mógł zamienić się w tysiące blach i odłamków. W wodzie (albo w skrzydle?) musiała być zatem torpeda lub bomba (na pewno termobaryczna!), odpalona  tak jak w Smoleńsku, gdy samolot już był metr od wody. No i nie wytrzymałem... ale od teraz naprawdę nie będzie żadnych komentarzy.

    MIG SŁABSZY OD TUPOLEWA?   NONSENS!

Skrzydła migów są, mówiąc potocznie, bardziej wytrzymałe na zderzenia z drzewami niż skrzydła tupolewów. Owszem, tupolew to samolot 5 razy cięższy, jego skrzydła mają większą powierzchnię i wytwarzają w locie poziomym po prostej 5 razy większą siłę nośną. Ale dla samolotu transportowego norma przeciążeń pionowych to ~2.5g, zaś w przypadku miga 9g, co automatycznie wymaga grubszych blach w (dodatkowo) geometrycznie cieńszych profilach skrzydła miga, co widać na ilustracjach powyżej. Dwa razy mniejsza wysokość profilu -> 2x większe siły na poszyciu, przy tej samej sile nośnej i tym samym jej momencie. Są i inne czynniki, które prześledzimy na przykładzie. Wyobraźmy sobie zderzenie z drzewem w okolicy gdzie skrzydło miga się mocno geometrycznie pogrubia i staje kadłubem nośnym (por. załączone zdjęcie, widać tam jak cienkie jest skrzydło). Na zewnątrz od tego miejsca jest mniej więcej taka rozpiętość skrzydła jak w urwanej końcówce skrzydła tupolewa, przypadkowo także cięciwy są b. podobne. W tej sytuacji, wobec tego, że lotnicze stopy aluminium mają zbliżone wytrzymałości na podstawowe rodzaje deformacji, blachy poszycia nośnego powinny być zaprojektowane w następującym stosunku grubości (mig:tupolew)

Stosunek grubości blach = (stosunek przeciążeń, tutaj 9/2.5) * (stosunek siły nośnej w locie nieprzyspieszonym na zewnętrznej części skrzydła, mniej więcej ~4 T w migu do 12 T w tupolewie) * (odwrotność stosunku geometrycznej grubości przekroju skrzydła,  około 2:1) ~ 9/2.5 * 4/12 * 2 ~ 2.4

Blacha poszycia miga w rozważanym miejscu powinna być ponad dwukrotnie grubsza od tej w tupolewie! Jeśli ktoś chce wiedzieć ile to milimetrów, co samo w sobie nie jest tu zasadnicze dla naszego porównania, będzie to grubość ok. 5 mm. Dodajmy do tego być może nieco niedokładnego oszacowania wymagania odporności materiału na szoki termiczne i mechaniczne przy przechodzeniu bariery dźwięku, przy postrzałach z broni pokładowej lub pociskami przeciwlotniczymi. Zrozumiemy wtedy wnet dlaczego faktycznie stosowane grubości blach użytych w kesonowej konstrukcji skrzydła myśliwca są nieraz 50% do 100% wyższe niż w transportowym i nieakrobacyjnym tupolewie [5], [8], [9], [10], [11].

Grubość blach i wytrzymałość kesonu na uderzenia przedmiotów zmniejszają się od miejsca mocowania w kadłubie do końcówki skrzydła, skąd wynika część zmienności wyników zderzeń. Ale ogólne twierdzenie, że samolot Mig-29 jest lekki i słaby w porównaniu z TU-154, jest odwrotnością prawdy. Do budowy płyt dźwigarów i poszycia w kesonowej, samonośnej konstrukcji skrzydła po prostu nie da się użyć w takim samolocie jak Mig-29 blachy cieńszej niż 3-4 mm.

    

      DRZEWA

O wyniku spotkania skrzydła z drzewem przy typowej prędkości podejścia 240-270 km/godz. decyduje nie tyle to, czy to skrzydło tupolewa czy miga, ale jakie i jak duże drzewo stoi tam, gdzie nie powinny one latać. A także to, w którą część skrzydła uderza pień. 

Największe pnie drzew napotykane przez skrzydła w lesie pod Mińskiem i Smoleńskiem nie były podobne. Nie tylko były z innego drewna, chodzi głównie o gęstość. Brzoza u swej podstawy, w kwietniu, ma około dwa razy większą gęstość, tylko o 5% niższą niż woda, i o kilkadziesiąt procent większą wytrzymałość na rozciąganie i zgniatanie od mińskich sosen i świerków, które są tak lekkie, że pływając po wodzie nie zanurzają się więcej niż w połowie. Pisałem o tym w tym blogu [16]. Nawet brzoza w zimie nie jest tak uwodniona jak w kwietniu, i może mieć gęstość najwyżej 70% gęstości wody (w przecince mińskiej zjadowały się cienki brzozy). Ale co ważniejsze, miały różne średnice. Proszę rzucić okiem na samo miejsce katastrofy i porównać z linijką w ręku średnice drzew z wysokością postaci tuż przy nich lub za nimi stojących. 

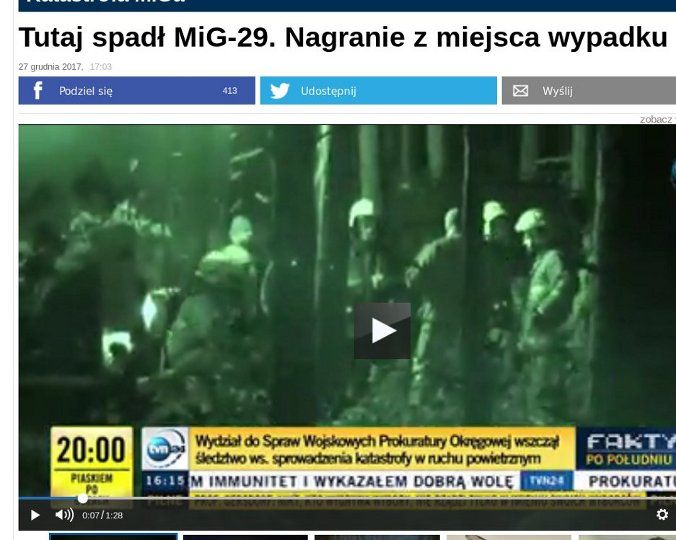
Drzewa w mińskim lesie były  w większości 15 do 20-centymetrowej średnicy - zwłaszcza wyżej nad ziemią niż pokazuje zdjęcie.

Dużo lepsze zdjęcia wywiesiła ostatnio TVP. Z nich, znając rozpiętość skrzydła samolotu Mig-19 równą 11.4 m, można oszacować, że drzewa, głównie sosny, ale też niektóre brzozy, mają maksymalną średnicę 21 cm.

Ponieważ w ostatnim stuleciu wielokrotnie ponawiano próby wytrzymałościowe pień-skrzydło w rozlicznych katastrofach lotniczych, wiemy empirycznie, że na ogół pnie o średnicy poniżej 20-30 cm były łamane bądź ścinane nie prowadząc do destrukcji skrzydła, zaś pnie grubsze niż 30 cm zazwyczaj uszkadzały znacznie i rozrywały skrzydła. Świadczą o tym zdjęcia robione po wypadkach, jak badania testowe NASA/FAA w latach 60tych. Cierpliwy czytelnik w tym odcinku bloga uzyska jasność dlaczego tak jest. Do roboty.

     CO SIĘ DZIEJE GDY SKRZYDŁO UDERZA W PIEŃ?

Rośnie szybko powierzchnia styku i siła oddziaływania (zgodnie z III prawem dynamiki, takiej samej wartości, przeciwnie skierowane siły całkowite pchają  skrzydło i drzewo). Odkształcenia z początkowo elastycznych stają się plastyczne. Ciało, które pierwsze zgromadzi naprężenia większe od krytycznych (ultimate strength) uznajemy za to, które poddało się destrukcji pierwsze. . Nie oznacza to, że będzie to jedyne takie ciało, tylko że zostanie strukturalnie naruszone pierwsze. Co tu oznacza 'strukturalnie'? Np. że pomijamy ewentualne uszkodzenia przednich ''slatów' (w j. pol. zwanych niesłusznie slotami, bo po ang. to slats nie slots, może lepiej już mówmy o skrzelach?). Rozpatrujemy wytrzymałość elementów nośnych, tj. zasadniczych elementów strukturalnych kesonu skrzydła. Wystające przed krawędź natarcia blachy skrzeli owiną się wokół pnia i zapewnią dużą powierzchnię styku pnia i skrzydła. Ich ewentualne pękanie nie zmienia nic, gdyż nie przenoszą zasadniczych naprężeń w skrzydle i nie są specjalnie mocno do niego przymocowane. Ciałem, które pierwsze podlega nieodwracalnemu uszkodzeniu, jest wgniatany w kierunku ruchu skrzydła pień drzewa. Drewno jest bowiem bardzo mało wytrzymałe na tego typu i kierunku odkształcenia. Wystarczy przyłożyć radialnie (w kierunku osi pnia) naprężenie rzędu 10 MPa, czyli ok. 100 atm, podczas gdy potrzeba 300-400 MPa (3000-4000 atm) by uplastycznić, a potem zerwać blachy aluminiowych stopów lotniczych.  Dlatego zajmiemy się najpierw drzewem.

Drewno jest silnie ortotropowe (nieizotropowe) i w zależności od tego w jakim kierunku działa naprężenie krytyczne, będziemy mówić o ścięciu jego pnia (naprężenia poprzeczne do osi pnia, towarzyszące deformacji ściskania i ścinania zgniatają na miazgę drewno, urywają włókna i zostawiają przełom bez dużych drzazg),  lub o jego złamaniu (pień wygina się, a naprężenia osiowe zgniatają włókna po stronie napierającego skrzydła, a rozciągają pień wzdłuż kierunku włókien). W złamaniu, na przykład w Smoleńsku i w Mińsku, powstają wzdłuż pnia duże drzazgi oraz pęknięcia, co widać na zdjęciach. Nasza analiza wyjaśni, dlaczego wypadki lotnicze koło lotnisk, na podejściu/odejściu, nie ścinają drzew (i konarów)  jak tępe miecze, a nadcinają tylko i następnie łamią drzazgowo te drewniane belki.

      VELUT ARBOR AEVO   

Żywe drewno składa się z mikroskopowych włókien złożonych z długich komórek celulozowych nasiąkniętych wodą związaną z celulozą i ligniną (drzewnikiem), a przy dużej jego wilgotności także częściowo wypełnionych wodą tam, gdzie normalnie jest powietrze [14]. Dzięki obecności powietrza drewno nie jest na ogół gęstsze niż 1 g/cm³ (sama celuloza waży ponad 1.5 g/cm³). Pod dostatecznie silnym naciskiem regularnie ułożone celulozowe ściany komórki składają się jak blaszane strefy zgniotu w samochodzie, ściskając wspierającą ligninę, i o czynnik ~10 także powietrze, a w końcu rwąc się i zamieniając z sprasowaną, gęstą miazgę trocinową. Deformacja ścian komórkowych była wielokrotnie badana. Bardzo dokładne badania zgniatania poprzecznego drewna świerków i sosen (tzw. drewien miękkich, ang. softwood) przeprowadzono w Lund w Szwecji. W pracy [4] na licznych wykresach podano zależność naprężenie-odkształcenie dla wielu przykładów niewzmocnionych (jak i dodatkowo wzmocnionych) belek. Na małe siły drewno pnia reaguje elastycznie, czyli liniowo i odwracalnie, a dla ponad-krytycznych odkształceń ten wykres wypłaszcza się opisując deformację plastyczną. Drewno przechodzi wtedy do wolno rosnącej wartości naprężenia podczas dużej kompresji poprzecznej. Inżynierowie materiałowi wzrost naprężenia ze stopniem kompresji nazywają utwardzaniem. Jest to naturalne zjawisko towarzyszące zmniejszaniu porowatości materiału komórkowego. Znikomemu z naszego punktu widzenia wgnieceniu do 3 mm towarzyszy już naprężenie do σ ~7 MPa. Przy interesujących nas, większych wgnieceniach do paru centymetrów, zaniedbując niewielkie utwardzanie odkształceniowe, z eksperymentów [4] wynika naprężenie zgniatania poprzecznego σ ~10 MPa  zarówno dla żywego, nasiąkniętego wodą drewna sosny jak i brzozy (w miarę postępującej kompresji, celuloza obu rodzajów drewna zaczyna jej stawiać coraz bardziej podobny opór). Szybkość zgniatania jest ważna dla wartości naprężeń. Zgniatanie typowe dla prędkości początkowej  rzędu ~70 m/s (w obu rozważanych wypadkach) jest szybkie i odpowiada parametrowi szybkości deformacji równemu dε/dt ~ 10³/s, a lokalnie większemu. Co ciekawe, przytoczone tu wyniki znane były od bardzo dawna w szkołach artylerii.

     A NIECH TO KULE BIJĄ

W bitwach morskich kule (wylatujące z luf szybciej niż latają samoloty podchodzące do lądowania) po doleceniu do przeciwnika raz przebijały burty jego okrętów, a innym razem nie. Artylerzyści nie umieli podać jasnych reguł gwarantujących przestrzelenie umocnień i ścian. Powołano na uniwersytecie w Metz we Francji artyleryjską komisję państwową i zbadano [13] wszystkie zależności na poligonie dla celów z ziemi, ziemi z kamieniami, cegły, kamienia, ale też i ze świerków i brzóz (okazy wzięte do prób miały też zbliżone właściwości mechaniczne). Ułóżmy kilka oczywistych wyrażeń na spowalnianie biegu kuli w nieruchomym materiale tarczy.

dv/dt =  -F/M,     gdzie F to siła między pociskiem a tarczą, M to masa pocisku, v - jego prędkość,

F = σ A,   gdzie σ  = naprężenie  działające na powierzchnię A=πr² przekroju poprzecznego kuli armatniej o promieniu r (powierzchnia styku nie jest płaska tylko półsferyczna, ale uwzględniając kierunki sił, składowa całkowitej siły skierowana wzdłuż wektora v jest dokładnie równa F=σA; tak samo będę później rozważać równoważną płaską powierzchnię skrzydła i siła F będzie składową wzdłuż kierunku ruchu).

Znaleziono też dobrze wyjaśniający głębokości penetracji zmierzone na poligonie wzór

σ  = σ_R (1 + v²/u²), 

gdzie σ_R  to naprężenie normalne do powierzchni tarczy, v = chwilowa prędkość pocisku względem tarczy, także w trakcie zderzenia,  zaś u = stała materiałowa, prędkość charakterystyczna zaistnienia znacznej poprawki proporcjonalnej do kwadratu chwilowej prędkości kuli v. Jak widać, naprężenie całkowite składa się z dwóch członów. Jeden (σ_R) jest niezależny od prędkości i opisuje proces gniecenia ścian celulozowo-ligninowych komórek drewna. Drugi składnik naprężenia równy jest  σ_Rv²/u², gdzie mamy dwie stałe wartości, które możemy zapisać łącznie, używając jednego parametru ρ, jako naprężenie dynamiczne w ośrodku o gęstości ρ: 

σ  = σ_R + σ_R v²/u² = σ_R + ρv²/2,    gdzie ρ = 2σ_R/u² 

Naprężenie dynamiczne ρv²/2 jest przejawem niezerowej inercji materiału tarczy. Tego wszystkiego nie rozumiano chyba jeszcze w pełni, gdyż narzekano na słabe zrozumienie podawanych empirycznych zależności w XIX-wiecznej pracy [13]. W XXI w. użyjemy drugiej równości w powyższym równaniu. Temperując parę razy ołówek, wyniki cytowane w [13] przeliczyłem do współczesnego układu jednostek otrzymując takie oto stałe (wgniatanie poprzecznie do włókien drewna świerkowego lub brzozowego w badaniach w Metz):

σ_R =  11.4 MPa,   u = 224 m/s,  ρ =  453 kg/m³ = 0.453 g/cm³. 

Otrzymana wartość gęstości ośrodka odpowiada całkiem dobrze gęstościom średnim przesuszonego drewna jakie badano we Francji, jak i gęstościom sosen i świerków w zimie w Polsce.

     PARAMETRY WYPADKOWE

Niech pierwsza liczba w parze wpisanej w nawias {x_m, x_s} opisuje wypadek pod Mińskiem Maz., druga - wypadek tupolewa.

Prędkość tupolewa 101 podczas wypadku (a więc początkową wartość zmiennej v) zaokrąglę do v₀ = 270 km/h = 75 m/s, a za prędkość Miga-29 przyjmę najmniejszą standardowo zalecaną przez podręcznik dla pilotów na podejściu końcowym do lądowania prędkość v₀ = 240 km/h = 67 m/s [15], jako że pilot lądujący awaryjnie w lesie miał kontrolę nad samolotem i leciał najwolniej jak mógł, z drugiej strony nie ryzykując przeciągnięcia i możliwego korkociągu. W mojej notacji

v₀ = {66.7, 75} m/s.

Za gęstość drewna podstawimy wartości odpowiednio dla sosen/świerków, oraz wilgotnej w kwietniu brzozy smoleńskiej (w tym miesiącu brzozy są najbardziej wilgotne, [16]):

ρ = {453, 950} kg/m³.

Poprawka do naprężenia σ_R na inercję drewna wynosiła ρv₀²/2 = {1, 2.67} MPa, dając razem z σ_R= 11.4 MPa wartość początkową naprężenia  {12.4, 14.1} MPa.

W miarę spowalniania ruchu skrzydła względem drzewa, σ powraca do σ = σ_R. Zmienność czasowa jest na tyle niewielka, a komplikacja obliczeń dynamicznych na tyle duża, że przyjmiemy poniżej stałe w czasie wartości średnich arytmetycznych dla dwóch wypadków:

σ = {12, 12.7} MPa.

W Metz wstrzeliwano kule dość znacznej średnicy 2r = 9 cali (tego rzędu wielkości są też grubości skrzydeł samolotów) w unieruchomione tarcze drewniane. To ostatnie nie odpowiada dynamice wypadków lotniczych, bo konary i pnie drzew w miejscu uderzenia nie są sztywno zamocowane. Cały uderzony mocno sektor brzozy, świerku czy podobnej mechanicznie do świerku sosny rozpędzany jest przez skrzydło podczas wbijania skrzydła w pień, co ogranicza głębokość zgniecenia drewna. Konieczne jest obliczenie dynamiki tego procesu, aby powiedzieć jak głębokiego zgniatania można oczekiwać i jakie są maksymalne siły i naprężenia w tym procesie. Gdy siły indukowane w skrzydle przez zderzenie okażą się większe niż krytyczne (a naprężenia przekroczą wytrzymałość na zgniatanie nośnego poszycia skrzydła) będzie to znak, że rozpoczęło się rwanie skrzydła. Na początek jednak pomińmy tę kwestię, powrócimy do niej później.

     DYNAMIKA ZDERZENIA

Nazwiemy symbolem R promień cylindrycznego pnia.  W Smoleńsku R = 22 cm, gdyż niedokładnie kołowy przekrój brzozy Bodina miał obwód odpowiadający promieniowi 22 cm na wysokości zderzenia. W Mińsku Mazowieckim przyjmę drzewo nieco grubsze niż moje oszacowanie ze zdjęcia (R  ~ 0.1 m).

R = {0.125, 0.22} m, czyli średnice odpowiednio 25 i 44 cm.

Symbolem x nazwijmy odchylenie dalszej ścianki zgniatanego bloku drewna od położenia przed zderzeniem, natomiast wyrażeniem qR  głębokość zgniecenia drewna, tj. na ile skrzydło wgryzło się w danej chwili czasu t w poruszający się blok drewna. Zmienna q(t)  to liczba bezwymiarowa z zakresu 0...2, lub inaczej - głębokość wgniecenia w jednostkach R (promień przekroju nienaruszonego pnia).

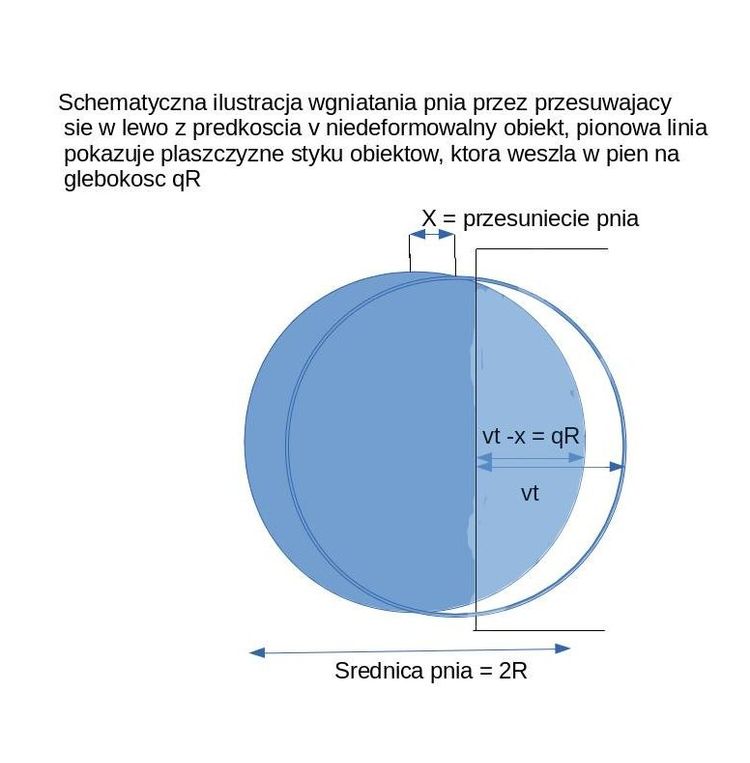
Fizyczna głębokość wcięcia skrzydła w pień po czasie t od pierwszego kontaktu ciał to

q R = v₀t - x                                                                                                            (1)

Chcemy zobaczyć, czy drzewo może być szybko zniszczone/zmiażdżone; w takim procesie jest wycinany z pnia cylinder o wysokości H równej grubości skrzydła. Pole podstawy koszonego cylindra oznaczmy jako początkowo wartość  πR²  oraz objętość  πHR² oraz masę m = πρHR².  W naszym modelu zgniatanie zmniejsza przekrój i objętość klocka drewna, ale nie zmienia jego masy m=const. Jaka to masa? Do tego najpierw musimy poznać wartość H. Gdyby chodziło o maksymalną grubość w środku profilu skrzydła, właściwie byłoby przyjąć {20, 35} cm, co byłoby zgodne ze średnią cięciwą skrzydła około c=3.5 m w obu przypadkach i stosunkiem spłaszczenia profili 6:100 oraz 1:10. Ale z drzewami zderza się cieńsza przednia część skrzydła, bliższa krawędzi natarcia. Przyjmę dlatego mniejsze o 25% wartości

H = {15, 26} cm.

Wtedy

m = {3.4, 38} kg

(Są to bardzo różne wartości intuicyjnie tłumaczące, dlaczego uzyskamy różne wyniki dla dwóch rozpatrywanych wypadków! Masa pnia jest bardzo ważna). Ułożymy teraz i rozwiążemy równanie różniczkowe na tempo zmian q(t), parametru głębokości wcięcia skrzydła w pień. Z równania (1) mamy różniczkując po czasie

dq/dt R = - dx/dt + v₀

a przy użyciu kolejnego różniczkowania i zasady dynamiki Newtona

m(d²x/dt²) = F = σ S(q),

gdzie S(q) to pole powierzchni styku, który w przekroju zaznaczyłem pionową czarną kreską a rysunku powyżej, dostajemy równanie na drugą pochodną czasową funkcji q:

 d²q/dt² = (-1/R) d²x/dt² = (-σ/mR) S(q),                                                            (2)

gdzie  m = πρHR² jak wyżej.

Z trygonometrii wyznaczamy formę S(q) przy upraszczającym założeniu, uzasadnionym uprzednio, że można za powierzchnię styku wziąć równoważną pionową  powierzchnię pracującą skrzydła, zaniedbując jej faktyczną krzywiznę. Tak się nota bene dzieje, kiedy po uderzeniu w pień slat/skrzela o dużej krzywiźnie deformują się, po czym uderza płaski pierwszy dźwigar. 

S(q) = 2 R H [q (2-q)]^1/2 .

Pole powierzchni styczności pnia i skrzydła jest zerowe gdy q=0 lub q=2, w maksimum S(1) = 2RH. Maksymalne pole styczności S osiągane jest po wgnieceniu połowy pnia (q=1); równe jest średnicy drzewa 2R razy H, co jest oczywiście prawdą w naszym modelu. Zdefiniujemy teraz stałą wielkość pomocniczą w,

w² :=  2σ/(πρR²)

której jednostką fizyczną jest [w]=1/s=Hz, oraz nową bezwymiarową funkcję φ(q) taką, że

dφ/dq := [q (2-q)]^1/2  ,                                                                                              (3)

przy użyciu których zapisujemy równanie różniczkowe (2) w uproszczonej postaci

d²q/dt² =  -w²dφ/dq.                                                                                               (4)

Jest to równanie ruchu cząstki w potencjale

w²φ(q) =w² ∫ [q (2-q)]^1/2 dq  =  (w²/2) [ arccos(1-q)  - (1-q) (q (2-q))^1/2 ]                     (5)

niezależnym od czasu. Dlatego rozwiązania mają całkę energii E = (dq/dt)^1/2/2 + w²φ(q) = const., wartość której wynika z konkretnych warunków początkowych zadania. Stąd otrzymujemy poszukiwane rozwiązanie na prędkość wgniatania

dq/dt  = [ (v₀/R)² - 2w²φ(q)  ]^1/2 .                                                                             (6)

Równanie (6) opisuje malenie bezwymiarowej szybkości q(t) zgniatania drewna, w miarę, jak parametr zgniatania q rośnie. Kiedy pochodna  dq/dt spada z początkowej wartości v₀/R do zera, pień przestaje być bocznie zgniatany, o ile wcześniej q nie osiągnęło wartości granicznej q=2, oznaczającej całkowite ścięcie pnia (sektor pnia zmiażdżony i wybity z drzewa dynamicznie). Ponieważ z (5) wynika φ(0) = 0, φ(2) = π/2, to sektor pnia jest całkowicie zmiażdżony i ścięty, gdy q=2, co wymaga: w < v₀ π^-1/2R^-1 lub inaczej: 

ρv₀²/2 > σ.

Jak widzimy, warunkiem ścięcia jest  przewaga efektów inercjalnych (w cieczach nazwalibyśmy je ciśnieniem dynamicznym, ang. ram pressure ρv²/2) nad wytrzymałością drewna na ściskanie prostopadle do włókien, σ.  Wiemy  z wcześniejszych rozważań o wartości poprawki na inercję, że jest ona liczbowo mała. Dlatego warunek ścinania/miażdżenia całego pnia nie był spełniony w omawianych dwóch katastrofach lotniczych i ogólnie rzadko bywa spełniony:

ρv₀²/2  = {1, 2.67} MPa    <<    σ = {12, 12.7} MPa.

Do całkowitego zgniecenia pnia potrzeba by bowiem prędkości zderzenia większej niż (2σ/ρ)^1/2 ~ {230, 164} m/s = {830, 590} km/h, a więc dużej, nie spotykanej w katastrofach na etapie podejścia do lądowania. To prędkość, przy której kawałek drewna rzucony o mur zostaje cały zmiażdżony i rozdrobniony.

Jak głębokie jest końcowe wgniecenie? Na to pytanie odpowiadają równania (5)-(6) i definicja w:

 φ(q) = (1/2) [ arccos(1-q)  - (1-q) (q (2-q))^1/2 ]  =  πρv₀²/(4σ)                         (7)

Po podstawieniu wartości liczbowych, w = {1.04, 0.419} kHz i równanie (7) przybiera postać

φ(q) = πρv₀²/4σ = {0.132, 0.330}    --->  q = {0.28, 0.53} --> największe wcięcie = q R = {3.5, 11.7} cm.

Pomocny tu jest wykres funkcji φ(q), a patrząc z boku także q(φ),  danych równaniem (7):

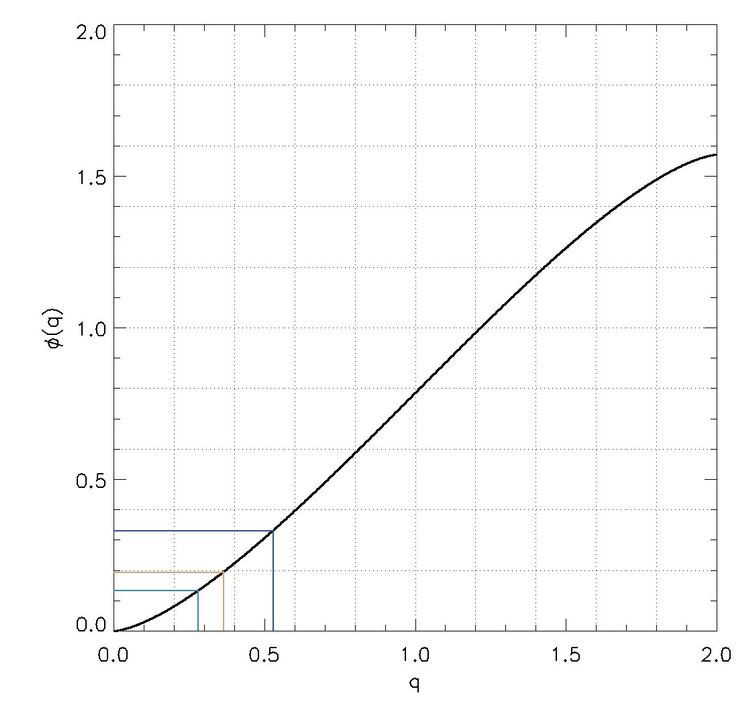
Model przewiduje, że pnie były wgniatane do głębokości 14% i 26% średnicy drzew, tj. do głębokości 3.5 cm w lesie pod Mińskiem Mazowieckim oraz 12 cm pod Smoleńskiem. Ta druga wartość na pewno nie jest zaniżona (wręcz przeciwnie, o czym wspomnę poniżej). Obie wartości są też zawyżone w przypadku drzew napotykanych przez Miga nie w pierwszej kolejności, gdy jego ruch został już spowolniony. Dlatego możemy mieć pewność, że podobnie jak w Smoleńsku, w lesie mińskim drzewa i konary były w niewielkim procencie pnia miażdżone/ścinane, a były mocno popychane tak, że wyginały się i po bardzo krótkim czasie ~10 milisekund łamały z pojawieniem dużych drzazg. Deformację można modelować przy użyciu teorii belki Timoszenki.

Na rysunku pokazałem też żółtą linią wartości odpowiadające cięciu drzewa brzozowego o gęstości 0.7 wody, grubszego niż spotykane na drodze Miga-29:  średnica 30 cm. Wtedy parametr q=0.365, odpowiadający wcięciu o głębokości do 5.5 cm.

     LOS SKRZYDEŁ

Pozostaje sprawdzić maksymalne naprężenie w skrzydle w czasie wgniatania pnia, aby przesądzić co stało się ze skrzydłem. Nie chcąc wydłużać notki nad miarę, nie będę przedstawiał tutaj modelu kesonu (można to naturalnie zrobić w oparciu o prawdziwe dane z biura konstrukcyjnego Tupolew, albo z oszacowań, które tu robiłem zanim red. Setlak opublikował dane w Przeglądzie Lotniczym). Pójdę na skróty i posłużę się znanymi siłami granicznymi. W  przedstawionym modelu największa siła towarzyszy największej powierzchni styku dwóch ciał, co następuje tuż przed zahamowaniem ich wzajemnego ruchu. Wtedy   q = {0.28, 0.53), a pole powierzchni pomnożone przez σ_R = 11.4 MPa (nie σ, ze względu na znikomy już wtedy dodatek naprężenia inercjalnego) daje maksymalną siłę oddziaływania F_max

 F_max= σ_R S(q) = 2 σ_R R H [q (2-q)]^1/2 = {30, 118} T

Zacznijmy od TU-154. Obliczenia grupy prof. Niezgody z WAT (Morka i in. [6]) mówią jasno, że przy prawidłowo dobranych grubościach blach w kesonie TU-154M, siła oddziaływania przy darciu skrzydła oscyluje wokół wartości  ok. 30 T << 118 T.  Nierówność ta gwarantuje, że skrzydło tupolewa było przerwane na brzozie, nie naderwane, ukręcone, czy jak tam niektórzy spekulują. Moje obliczenia następującego równolegle procesu gięcia brzozy w modelu belki Timoszenki, który uwzględnia zwężający się ku górze kształt pnia zakotwiczonego w ziemi, dynamikę zderzenia, deformacje wszelkich typów (rozciąganie, ściskanie, ścinanie i bezwładność liniową i obrotową elementów brzozy), przewidują, że przy sile ~30 T brzoza wygięła się i pękła na dwóch wysokościach: 6.5m i tuż nad ziemią. Tak faktycznie się stało [7]. Jeśli skrzydło urywa się, maksymalna siła w naszym modelu zgniatania nigdy się nie materializuje - już przy zgnieceniu pierwszych paru centymetrów pnia osiąga wartość rzędu 30 ton wystarczającą do urwania końcówki skrzydła i na tych paru centymetrach wgniecenia proces się kończy. Ponieważ prawdziwa struktura deformowanego skrzydła nie jest jednorodna, niektóre blachy wbiły się głębiej niż średnia głębokość paru centymetrów. Jeśli brzoza byłaby dwukrotnie cieńsza, model przewiduje taki sam procent wgniecenia pnia q (gdyż prawa strona równania (7) nie zależy od R), ale  także przewiduje siłę maksymalną powyżej 30 T. Brzoza w kwietniu jest większym zagrożeniem niż równie gruba sosna w grudniu, gdyż jest masywniejsza.

Jak stwierdziłem wcześniej, skrzydło samolotu Mig-29 jest średnio 1.5 do 2 razy "mocniejsze", tj składa się z tylokrotnie grubszych blach niż w tupolewie 154 (przeciętnie, chociaż dobrze jest porównywać konkretne miejsca uderzeń, a wtedy oszacowanie daje czynnik 2). Można spodziewać się, chociaż lepiej byłoby potwierdzić to dokładniejszymi obliczeniami FEM (MES) takimi jak w [6], że to przekłada się na w podobnym stopniu większą wymaganą siłę F przy destrukcji skrzydła ~50-60 T. Po prostu geometria pozostaje podobna, a siły skalują się liniowo z grubością blachy. Wyniki które tu uzyskaliśmy (mkasymalnie ~30 T siły przy zderzeniu z sosną lub świerkiem o średnicy pnia 25 cm) mówią o tym, że takie drzewo nie zagroziłoby integralności skrzydła Mig-29, ale już nieco większe mogło:  ponad 30-centymetrowe mogło je odciąć. Przeliczony wariant zderzenia miga z brzozą o średnicy 30 cm przewiduje siłę  F_max= σ_R S(0.365) = 40 T, więc jeszcze nie łamiącą skrzydła Miga.

Wszystko zależy naturalnie od tego, w którym jego miejscu doszłoby do zderzenia; na kadłubie tuż przy skrzydle blachy są tak grube, że bez wątpienia wystąpi siła przekraczająca 45 T lub 60 T przy ich ewentualnym rwaniu, natomiast nie jest jasne czy uderzenie nawet 25-centymetrowego drzewa przetrwałaby np. króciutka końcówka skrzydła myśliwca. (Przypominam, że nie wiemy jeszcze ani czy faktycznie skrzydła samolotu przetrwały strukturalnie koszenie lasu, ani czy na konkretnej drodze hamowania miga znalazło się drzewo przekraczające 30 cm średnicy na wysokości zderzenia, gdzie ewntualnie trafiło końcówkę skrzydła itp. - zapewne nie było tak dużych drzew na drodze miga i skrzydła przetrwały katastrofę, gubiąc jedynie skrzela i klapy).

Nasz model, jak każde obliczenie teoretyczne, robi wiele założeń i może nie być bardzo dokładny, dopóki nie zostanie potwierdzony doświadczeniem. Być może najgorszym założeniem była jednorodna struktura i skrzydła i brzozy przy ich styku (argumentowałem że naprężenia są tam homogenizowane przez obecność zdeformowanych blach skrzeli, ale nikt tego na pewno nie wie). Gdyby komuś chciało się model uściślać i komplikować, ciekawym lecz akademickim pytaniem byłoby jaka jest konkretnie średnica najcieńszej brzozy (lub innego drzewa) które może urwać końcówkę skrzydła TU-154 taką, jak w Smoleńsku. To w co już możemy zaufać na podstawie prostego modelu, ponieważ kryteria są spełnione z dużym zapasem, to fakt, że wilgotna brzoza Bodina o średnicy 44 cm wystarczyła z dużym zapasem do destrukcji skrzydła samolotu pasażerskiego. Wiemy też, że drzewa z mniej gęstego drewna o mniejszej średnicy 20 i 25 cm (pnie  8-do 10 razy lżejsze) nie rwą skrzydeł myśliwców takich jak Mig-29. 

 

     KONKLUZJE MODELU.  AWARIA MIGA.

Jak widać, żadnej sugerowanej dziwności czy tajemnicy Smoleńskiego łamania brzozy ani żadnej macierewiczowskiej "zbieżności" pomiędzy wypadkami mińskim i smoleńskim nie było. Prawdziwa fizyka nie wnosi zastrzeżeń do rzeczywistości. W przypadku samolotów komunikacyjnych połówka, a być może nawet ćwiartka objętości pnia brzozy Bodina mogła spowodować urwanie końcówki skrzydła,  czyniącj samolot niesterownym.

W Mińsku Mazowieckim, tak jak w Smoleńsku zrobiona została przecinka w rzadkim lesie. W odróżnieniu od Smoleńska, nie było tam na drodze samolotu drzew o średnicy powyżej powyżej 25 cm z gęstego, uwodnionego drewna brzozy. Było dużo 10-20 cm sosen, które łamiącymi się gałeziami i pniami wyhamowały samolot. Tymczasem skrzydło miga było dwukrotnie mocniejsze i prawdopodobnie przetrwało. Wypadki miały zgodnie z fizyką i inżynierią materiałową bardzo różny przebieg i zakończenie.

Porównanie nie pokazuje wcale, że tupolewem można kosić las smoleński. Lot tym samolotem parę metrów nad ziemią, jak dnia 10.04.10, nawet wśród 20-centymetrowych drzew nie jest godny polecenia. Na pewno tupolew skosi 10-centymetrowe konary i pnie, ale nie podjąłbym się koszenia nim niczego więcej. Ogólnie, lepiej takich prób unikać. Gałęzie lubią blokować powierzchnie sterowe, a nawet pięciocentymetrowe drzewko na drodze kokpitu może skomplikować dalszy lot kasując pilotów. Proponuję trzymać się minimalnych wysokości zniżania, chyba że jest awaria.

Może była pod Mińskiem, a może zabrakło paliwa. Świadek naoczny mówił o dymie ciągniętym przez samolot, ale nie wiem jak gęstym, bo ros. myśliwce i tupolewy trochę kopcą i mógł się pomylić widząc spaliny z bliska. To byłaby rzadkość: awaria wyłączająca oba silniki. Wg podręcznika dla pilotów [15], lądowanie Miga-29 z jednym zepsutym silnikiem nie różni się niemal od normalnego.  Ma taki nadmiar mocy, że nie jest to sytuacja awaryjna (to samo Tu-154, startuje i ląduje bez jednego silnika tak, że nikt tego nie zauważa). Po zbadaniu wraku niech wypowiedzą się specjaliści - ci jeszcze nie wyrzuceni z pracy w obecnie zmilitaryzowanych jak za stanu wojennego komisjach badania wypadków.

POST SCRIPTUM

Trzy dni po publikacji tego tekstu min. Macierewicz został zdymisjonowany.

LlTERATURA CYTOWANA

[1] Gwiazdę Betlejemską i wizytę magów omówiłem w https://www.salon24.pl/u/fizyka-smolenska/375846,czym-byla-gwiazda-betlejemska

[2] "Cały praktycznie samolot był porozrywany, drzewa były połamane, odłamki były porozrzucane na pewną odległość" powiedział Piotr Serafin, Nadleśniczy Nadleśnictwa Mińsk.  Fakty, TVN 20 grudnia 2017. https://www.tvn24.pl/wiadomosci-z-kraju,3/wiceszef-mon-o-katastrofie-mysliwca-pilot-mig-29-nie-katapultowal-sie,800074.html

[3]  http://www.nowydzwon.pl/2017/07/mannerheim-uhonorowany/

[4] D. Ed & F. Hasselqvist, "Timber compression strength perpendicular to the grain", Dept. Struct. Eng., Lund Inst. Techn. 2011, http://lup.lub.lu.se/luur/download?func=downloadFile&recordOId=3159865&fileOId=3159867

[5] Odnośnik do grubości blach nośnego mechanicznie pokrycia skrzydła w F35: https://www.compositesworld.com/articles/skinning-the-f-35-fighter

[6] A. Morka et al., referat na 2 konf. smoleńskiej.

[7]  P. Artymowicz referat na konf. Mechanics in Aviation 2014, http://planets.utsc.utoronto.ca/~pawel/MechAvXVI-2.pdf , Kazimierz Dolny, Polska.

[8] Stopy aluminium używane w skrzydlach tupolewa (D16) są zbliżone właściwościami do 2024-T3, małe części do stopów z serii 7000. Natomiast myśliwce mają bardziej wytrzymale stopy aluminium o nieraz bardzo dużej grubości (zob [11]):

Traditionally, the structural aluminum alloys in aircraft have been 2024 in damage-critical areas and 7075 in strength-critical areas (Starke and Staley, 1996).

High wing loadings, which dictate thick wing skins, typically 0.5 to 1.5 in. at the root. Alloy 7075-T6 has been the workhorse, complemented in specialized applications by 2014-T6, 2024 in both naturally and artificially aged tempers, 7079-T6, and 7178-T6. Innymi słowy, poszycie skrzydła w Migu miało prawdopodobnie 1.3 do 3.5 cm grubości koło kadłuba, więcej niż w przypadku skrzydła tupolewa.

[9] Nieco mniejszy od Mig 29 myśliwiec F-16 ma aluminiowe panele kadłuba o grubości stopu 3.2-12.7 mm. To bardzo dużo, w porównaniu z tupolewem. Cytuję za: https://www.quora.com/What-is-the-average-thickness-of-fuselage-skin-panels-on-the-F-15-and-F-16. The fuselage skin thickness for the F-16 varies from 0.125 inches to 0.5 inches. [od 1/8 do 1/2 cala, czyli 3.2 mm do 12.7 mm. Podobnie zresztą skrzydło. Dla porównania, kadłub tupolewa jest znacznie cieńszy, ma nie więcej niż ~2 milimetrów grubości. 

[10] http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.666.2311&rep=rep1&type=pdf,  A comparison of metallic and composite aircraft wings using aerostructural design optimization, Kennedy and Martins, 2014.

[11]  Porównanie grubości paneli samolotow transportowych i myśliwskich (które w szczegółach są tajemnicą producenta i odbiorcy, więc są to dane przybliżone) można znaleźć m.in. w  http://www.totalmateria.com/Article96.htm

Transport aircraft of the types operated by commercial airlines: For wing tension members, shear webs, and ribs, alloys 2014-T6, 2024-T4, and 7075-T6 are used. Rolled sheet and plate 0.040 to approximately 0.375 in. thick are employed for wing skins [po pol.: od 1 mm do 4.75 mm, w przypadku żeber i płyt dźwigarów samolotów komercjalnych]. Fuselages:  Alclad sheet 0.040 to 0.187 in. thick in 2014-T6, 2024-T3, 7075-T6, and 7079-T6 is utilized  [główna część kadłuba to blachy o grubości od 1 do 4.8 mm].

[12] Można powiedzieć, że drewno ma konstrukcję mikro-kesonową, a skrzydło podobną, tyle że aluminową, o olbrzymich ~30-centymetrowych komórkach z bardzo cienkimi ścianami, prawie pustą w środku. Nie powinno to dziwić, gdyż są to optymalnie przeewoluowane, jak najlżejsze, maksymalnie wytrzymałe na siły aerodynamiczne obiekty. Drzewa muszą wytrzymać wielkie siły kompresujące włókna giętego przez wiatr pnia po zawietrznej i rozciągające po stronie nawietrznej. Dlatego wytrzymałość (pod którą będziemy tu rozumieć graniczne naprężenia) wzdłuż włókien w giętym pniu musi być znacznie wyższa niż na zgniatanie w poprzek włókien, biegnących pod pewnym niewielkim kątem do pionu. Wytrzymałość na rozciąganie mierzy MOR, modulus of rupture (moduł zrywania), który jest znany. Mokre drewno brzozy lekarza Bodina miało wartość w zakresie MOR = 50-70 MPa, a świerki i sosny mińskie niewiele mniej; można przyjąć do szacunków 40-60 MPa, to znacznie więcej niż ~10 MPa przy obciążeniu radialnym (horyzontalnym, bocznym) belki pnia.

[13] W. Johnson's Universal Cyclopaedia, Vol. IV,  pod red. C. K. Adamsa, New York 1896,  str. 79.  Najdokładniejsze badania głębokości penetracji drewna, ziemi i muru przez kuliste pociski przeprowadziła w Metz w r. 18134 i 1835 komisja francuskiego Ministra Wojny. W pierwszej połowie XIX w. odbywały się liczne bitwy morskie i znajomość takich wielkości była niesłychanie potrzebna i do budowy i do dziurawienia drewnianych okrętów. Na tej podstawie odtworzono następującą regułę empiryczną penetracji drewna brzozy i świerku (nieco inaczej liczbowo wyglądały współczynniki w przypadku innych rodzajów drewna): siła oporu tarczy rośnie z kwadratem średnicy pocisku D pomnożonym przez σ (1 + (v/u)² ), gdzie σ,  u  są stałymi zależnymi od materiału tarczy, a v to prędkość. Tabelkę wartości stałych podał Didion, dla brzozy i świerku (nieco inaczej liczbowo wyglądały współczynniki w przypadku innych rodzajów drewna, ale na pewno sosna nie jest bardziej wytrzymała od świerku, zatem można brać dane świerku do obliczeń). Mamy, po przeliczeniu na nasze obecne jednostki układu SI: σ = 11.4 MPa, u =224 m/s. 

[14] Nonlinear mechanical behaviour and analysis of wood and fibre materials, S. Holmberg et al., Computers and Structures 72 (1999), 459-480.  http://planets.utsc.utoronto.ca/~pawel/wood-nonlin.pdf

[15] Prakticzeskaja aerodinamika samoleta Mig-29. Uczebnoje posobije, 1995

[16] Liczne fakty z mechaniki drewna zawarte są w odcinakach tego bloga i odsyłaczach, m.in. w https://www.salon24.pl/u/fizyka-smolenska/353350,12-coraz-dluzszy-cien-brzozy