74. Telefon satelitarny. 75. Fizyczne skutki uderzenia w ziemię - 100g

(74.) Z zapisu telefonu satelitarnego (przez który Kaczyńscy rozmawiali przed wypadkiem) wynika, że zasilanie z sieci elektrycznej samolotu było ciągłe aż do momentu uderzenia w ziemię i dezintegracji samolotu koło salonu samochodowego KIA za szosą Kutuzowa. Nie było wybuchów ani rozpadu samolotu w powietrzu.

(75.) Analiza fizyczna uderzenia w zimię w lutu PLF 101 jednoznacznie pokazuje, dlaczego wypadek był nonsurvivable (nie do przeżycia). M.in., na ciała pasażerów działało przyspieszenie rzędu 100g, wcześniej poprawnie określone przez patomorfologów.

Rozdział 74:    TELEFON  SATELITARNY  SIECI  INMARSAT

Pamięć telefonu Aero-HSD+ przez który rozmawiali bracia Kaczyńscy niedługo przed feralnym końcem lotu PLF 101, przetrwała katastrofę. Treść automatycznych zapisów telefonu świadczy o tym, że urządzenia pokładowe tupolewa nr. 101 miały nieprzerwane zasilanie z sieci elektrycznej samolotu do samego momentu jego fragmentacji na polu rozpadu. To kolejny dowód materialny wykluczający politycznie motywowane oszustwa "podkomisji" PiS o tym, jakoby w samolocie nastąpiła seria wybuchów i doznał on fragmentacji w powietrzu.

Zachowały się dobrze dwa bloki główne telefonu satelitarnego sieci Inmarsat, AERO-HSD+ Thrane&Thrane. Telefon jest zasilany prądownicą samolotu i tylko w przypadku przerwania zasilania przełącza się na własną baterię, zapisując ostrzeżenie o tym w logfile. W logfile'ach bloków HSD i H+ nie ma śladu przerwania zasilania samolotowego nawet w czase zderzeń PLF 101  z drzewami,  do momentu następującego krótką chwilę po katastrofalnym w skutkach przyziemieniu. 

10.04.2010 06:41:03.481 WARNING:* Idle:1:Power fail event 1: VIN bad (PFH disabled)
10.04.2010 06:41:03.530 WARNING:* iTM:1:Power fail event 2: power fail (PFH disabled)

10.04.2010 06:41:05.808 WARNING:* Idle:0:Power fail event 1: VIN bad
10.04.2010 06:41:05.857 WARNING:* HpaOut:0:Power fail event 2: power fail.

Zasilanie samolotowe telefomu przetrwało cały "zamach" i wielokrotne wybuchy postulowane przez oszustów z PiS. Zobacz cały tekst o telefonie satelitarnym tutaj.

Nic dziwnego, że gdy po szczegółowej analizie przeprowadzonej na podstawie przekazanych im oryginalnych danych o wypadku swe opinie złożyli Macierewiczowi w grudniu 2019 r. i styczniu 2020 r.  eksperci angielskiej i szwedzkiej komisji badania wypadków lotniczych:  Christopher Prothero, Goran Lilja oraz Christer Magnusson,  Antoni M panicznie ukrywa te ekspertyzy, gdyż prawda w nich zawarta odsłania jego matactwa. Powinien zresztą zostać postawiony przed sądem w związku z nielegalnymi naciskami i próbami wymuszania zmiany ich opinii. Ale to jest Polska. A teraz przejdźmy do technicznej analizy przeciążeń i szans przeżycia pasażerów, której nie pozwala mi mimo 3 publikacji i 7 listów do redakcji umieścić w dziale kwS administracja.

  Rozdział 75:      CZY  PASAŻEROWIE  MOGLI  PRZEŻYĆ  KATASTROFĘ  PLF 101?

Zasadniczym pytaniem w każdej dużej katastrofie jest "dlaczego ludzie zginęli". Nie wchodząc w szczegóły stanu konkretnych ciał (to robi w salonie24 stanzag, zakładam że dobrze), rozważymy często wspominaną kwestię czy pasażerowie mogli przeżyć katastrofę smoleńską w warunkach fizycznych towarzyszących spadkowi PLF 101 na ziemię. Oszacujemy przyspieszenia.  W ich analizie bywały w przeszłości robione rażące, grube błędy. Przeanalizujemy też inne warunki konieczne do przeżycia. To wyczerpująco odpowie na tytułowe pytanie. Wypadek smoleński był, jak mawia NTSB, unsurvivable, tj. nie dający możliwości przeżycia.

  75.1.  SPADEK  NA  ZIEMIĘ.  SKŁADOWE  PRĘDKOŚCI:  70 m/s  i  20 m/s

Zgodnie z fizycznymi obliczeniami trajektorii zaprezentowanymi w rozdz 30 , 32 i 33, zderzenie PLF 101 z ziemią zaszło przy ułożeniu kadłuba pod kątem -6 stopni do horyzontu, ze składowymi prędkości ok. 70 m/s poziomo i ok. 20 m/s pionowo. Skąd taka duża wartość prędkości pionowej? Stąd, że mimo iż kąt natarcia spadł pod koniec lotu PLF 101 z dużych wartości tuż za brzozą Bodina przekraczających 12 stopni (gdy było duże pochylenie kadłuba i produkowane były znaczne przeciążenia (ściślej: obciążenia) równe 1.36 g za brzozą Bodina, do małych wartości (-2 stopnie), to cały czas skrzydła wytwarzały siłę aerodynamiczną skierowaną normalnie tj. wciskającą pasażerów w fotel (obciążenie ~0.4 g). [Z definicji AoA wynika, że w TU-154 z klapami 36 stopni dopiero przy AoA poniżej  -6.5 stopnia siła aerodynamiczna pcha kadłub samolotu "w dół", w kierunku podłogi a nie sufitu.] Czyli spadek z maksymalnego wzniesienia samolotu  koło autokomisu między ul. Gubienko a ul. Kutuzowa nie był spadkiem swobodnym, a spadkiem nieco przyspieszonym przez siłę nośną skierowaną w dół, przewyższającą opór. W momencie pierwszego kontaktu lewego kikuta skrzydła i statecznika pionowego V_z = -18 m/s, ale gdy duża część kadłuba uderzała w ziemię, było już V_z = -20 m/s. To tak, jakby samolot został zrzucony swobodnie z wysokości V_z²/2g = 20 m, czyli piątego piętra. To dużo więcej niż w jakichkolwiek testach FAA, gdzie największe badane prędkości wynosiły V_z = 35 ft/s ~ 10 m/s (jak w spadku swobodnym z wys. 5 m). W Uzupełnieniu podaję uzasadnienie skalowania przeciążeń z prędkością typu a ~ V_z^3/2. Wg tej zależności, spadek w Smoleńsku powinien skutkować 3 razy większymi przyspieszeniami działającymi na pasażerów niż w najbardziej destrukcyjnych testach FAA/NASA. Dodatkowo, nigdy nie były testowane spadki w pozycji odwróconej, a to jak zobaczymy poniżej ma bardzo poważne konsekwencje.

  75.2.  MYLNE  OSZACOWANIA  PRZYSPIESZEŃ

To klasyczne zagadnienie smoleńskie, na którym rozłożyli się nie tylko (1) Macierewicz wraz z podkomisarzami ludowymi,  (2) ludzie niezbyt normalni twierdzący, iż "nie było żadnej katastrofy", (3) nowy ekspert Gazety Polskiej (ros. palacz kotłowy i pisarz Sołonin), ale także i (4) minister Miller i jego komisjanci rozmawiający o przyspieszeniach w nagraniach z posiedzeń KBWLLP.  Oto wzorzec błędnego  oszacowania, powielany w salonie24:

"Chcę oszacować przyspieszenie a, czyli F/m. Siła F=ma  razy  droga hamowania S  to praca, zmiana energii. Chodzi tu o spadek en. kinetycznej z   mV²/2   do zera, gdzie V to prędkość początkowa ruchu poziomego (V~70 m/s).  Zatem  aS = V²/2.  Średnie przyspieszenie równe jest więc  a = V²/(2S).  Średnia droga hamowania części samolotu była rzędu S~100 m, ponieważ taki jest odstęp od pierwszych bruzd  w ziemi do środka pola rozpadu. Wychodzi a =  70²/200 m/s² ~ 2.5 g. Raporty komisji badania wypadków kłamią, że  a ~ 100 g!"

Pomyłka bierze się z pokręcenia pionu z poziomem i ze złej wartości S. Zamiast brać drogę hamowania elementów samolotu i części ciał pasażerów w kierunku pionowym (najkrótszego hamowania), błędne rozumowanie rozważa tylko hamowanie w kierunku poziomym. Nawet w tym kierunku oszacowanie opiera się na błędnej średniej, nie uwzględniając że hamowanie w poziomie było niejednostajne, osiągało najbardziej znaczące wartości przy lokalnym hamowaniu na przeszkodach i nierównościach terenu, a także podczas wyginania konstrukcji, Mylnie wzięto zatem średnią wartość S~100 m zamiast poprawniejszą S~2 m opisującą największą średnią krótkookresową. Hamowanie ruchu pionowego odbyło się na jeszcze mniejszej drodze. Prawidłowe oszacowanie różni się od nieprawidłowego o dwa rzędy wielkości.

  75.3.  SZACOWANIE  PRZYSPIESZEŃ  CZĘŚCI  SAMOLOTU

Policzmy najpierw jakie przyspieszenia działały w związku z dużym uderzeniem pionowym w grunt na samolot, kiedy jeszcze był w całości i mało zdeformowany. Nota bene, nie będę purystą i nie będę rozróżniał 'przyspieszeń' od 'opóźnień' (ani 'kadłuba' od 'części kadłuba' - wiadomo z opisu świadków naocznych, że kadłub natychmiast po upadku przerwał się na trzy a potem więcej części). Gliniasty grunt smoleński poddawał się silnemu uderzeniu w modzie deformacji nie takiej jak wtedy kiedy kładziemy się na ziemi lub po niej skaczemy, elastycznej, lecz deformacji plastycznej. Grunt osiągnął maksymalne naprężenie σ, po czym przy stałym naprężeniu σ odkształcał się dalej plastycznie. Naprężenie quasi-statyczne ma wartość rzędu σ ~ 1 MN/m², tj. 1 MPa. (Omawiałem dokładnie geotechnikę gruntów przy okazji problemu wbijania drzwi 2L. Polecam ilustracje z pomiarów naprężenia plastycznego w rozdz. 68.)

Dodatkowo, są też efekty związane z ruchem: szybkość deformacji materiału daje człon naprężenia proporcjonalny do kwadratu prędkości, zwany członem inercjalnym, równy ρv²/2 (wartość ta odpowiada dosłownie ciśnieniu dynamicznemu plastycznego gruntu o gęstości ρ i została po raz pierwszy opisana przez Newtona). Sumując dwa człony, otrzymujemy przyspieszenie takie, jak w opracowaniu Jean V. Poncelet'a (Cours De Mechanique Industrielle, wyd. 1sze,  1829) gdzie omawia głębokości penetracji pocisków w ziemi:

a = (σ +  ρ v²/2) (A/M) = (σ A/M) [1 + ρv²/2σ]                                          (1)

gdzie A/M jest stosunkiem powierzchni kadłuba do jego masy (weźmiemy orientacyjne, okrągłe liczby 60 ton masy i 60 m² powierzchni styczności z ziemią). Jeśli chodzi o człon inercjalny, kwadratowy w prędkości, to jego forma odpowiada przyjęciu współczynnika Ponceleta C=1/2, równoważnego współczynnikowi oporu czołowego C_d=1 (por. Bless, Omidvar & Iskander, https://aip.scitation.org/doi/pdf/10.1063/1.5044920 ; to praca o oporze ruchu w suchym piasku, lecz człon inercjalny jest taki sam i w przypadku mokrej gliny i każdego upłynnionego naprężeniem gruntu). Naprężenie plastyczne przekracza czterokrotnie efekt inercjalny przy v = V_z = -20 m/s, w nawiasie kwadratowym wzoru (1) mamy wtedy wartość 1 + 1/4. Dla uproszczenia pominę więc efekt inercjalny zależny od v (oszacowania nie są aż tak dokładne by to uwzględniać, mamy bowiem sporą nieoznaczoność iloczynu σA). Minimalne przyspieszenie, zaniedbujące umiarkowane efekty inercjalne gruntu przybiera postać

a ~ σA/M ~ 1000 m/s² ~ 100 g.

Pionowe uderzenie w grunt smoleński powoduje przyspieszenia na strukturze samolotu co najmniej rzędu 100g (z dokładnością do czynnika 2). Zauważmy przy okazji, że to odpowiada prędkości pocz. 20 m/s i drodze jednostajnego hamowania S = 0.2 m, co faktycznie jest bliskie średniej głębokości, na którą grunt ugiął się pod samolotem (por. tekst  o braku krateru).

Uwzględnimy dwa czynniki mające przeciwny wpływ na przyspieszenia. Pierwszy taki, że droga hamowania ruchu pionowego foteli pasażerów może być większa niż plastyczne wgłębienie pozostawiane przez sztywny kadłub w gruncie. Chodzi o

Amortyzujące działanie struktury kabiny pasażerów - przypadek idealny

Ponieważ struktura kadłuba też staje się plastyczna, gnie się i rozrywa, pochłania część energii spadku zmniejszając przeciążenia. Największa, optymalna deformacja, która daje najdłuższą możliwą drogę hamowania i jednocześnie nie zgniecie pasażerów w odwróconym samolocie, jest rzędu ~1 m, ale taka wartość jest mało prawdopodobna (dlaczego bowiem faktyczne wgięcie wręg o średnicy 4 m nie miałoby być 0.25 m albo 3 m?)  Z ostatecznymi wnioskami musimy zaczekać do podrozdziału traktującego o tym co dzieje się z fotelami lotniczymi. A tu sumując 20 cm zagłębienia w gruncie i prawdopodobnie jeszcze  bezpieczne ze względu na możliwość zgniecenia pasażerów gięcie konstrukcji nad ich głowami o wartość 3 razy większą, możemy oszacować że absolutne minimum przeciążenia podłogi kabiny pasażerskiej mogło wynosić    a ~ (20 m/s)²/(2*0.80m) ~ 25 g  w nierealistycznym przypadku, jak będę argumentował niżej, gdy gięcie konstrukcji wydłuża znacznie drogę hamowania gdyż jest duże, prawie tak duże, iż zgniata pasażerów. To przypadek idealny przy spadku odwróconym, na który samoloty NIE są projektowane i takie gięcie w Smoleńsku nie wystąpiło, o czym świadczy stan ofiar wypadku. Po prostu chciałem pokazać, że nawet  minimalne przeciążenie konstrukcji foteli jest zabójcze (por. podrozdz. 75.4).

Ruch poziomy

To drugi efekt, który trzeba uwzględnić. Około 12-krotnie większa energia związana jest z ruchem poziomym, dotychczas przez nas zaniedbanym. Hamowanie ruchu poziomego było bardzo nierównomierne. Hamowanie  samolotu na płaskiej płycie lotniska hipotetycznymi najlepszymi hamulcami i oponami świata (dającymi opóźnienie ~1g), albo ślizganie się po ziemi ze wsp. tarcia  równym 1, dającym opóźnienie 1g , odbyłoby się na drodze znacznie większej niż odległość centrum wrakowiska od pierwszych bruzd na ziemi: s ~ (V²/2g) ~ 250 m >>  ~100 m. To argument, że w Smoleńsku ślizg zasadniczych części samolotu po ziemi był przerywany nagłymi epizodami uderzeń w przeszkody. Jest to tym bardziej prawdą, jeśli kontakt części samolotu z ziemią nie był ciągle utrzymany (np. następowały odbicia od ziemi i część drogi odbywała się z małym przyspieszeniem w powietrzu). Nie będziemy nigdy w stanie odtworzyć położeń drzew i pagórków w oryginalnym lesie sprzed 10 kwietnia 2010 r., dlatego trudno powiedzieć coś więcej konkretnie. Wiadomo jednak, że gdy mała część samolotu lub ciało człowieka napotyka na przeszkodę (np. drzewo) dającą drogę hamowania x  ~ 0.5 m z prędkości pocz. V = 70 m/s, wtedy przyspieszenie może sięgać nawet

a_x ~ (V²/2x) ~ 5000 m/s² ~ 500 g.

Zaś te części, które zakopują się z dużą prędkością w ziemię w nierównym terenie albo są zanurzane pod grunt w wyniku działania składowej pionowej siły, będą miały decydujący wkład od czynnika inercjalnego w równaniu (1). Przy gęstości gruntu 1700 kg/m³ i przyjmując przykładowo sektor kadłuba o długości 4 m i przekroju uderzającego w ziemię A = 2.5 m²  (20% całego przekroju kołowego),  M  = 3400 kg, otrzymamy przyspieszenie

a_xz  ~ (A/M) (ρV²/2) ~ (2.5/3400) 1700 *  2500 m/s² ~ 300 g

co wskazuje na natychmiastową destrukcję segmentu. Zatem rozważywszy proces ostrego hamowania części samolotu wbijanych w ziemie przez ruch w pionie i w poziomie, możemy być pewni, że przyspieszenia mierzone na elementach konstrukcyjnych i fotelach zamocowanych na sztywno na podłodze,  w czasie fragmentacji samolotu byłyby typowo rzędu 10² g.

  75.4.  PRZYSPIESZENIA  CIAŁ  PASAŻERÓW

NASA wraz z FAA badały wielokrotnie jakim przyspieszeniom poddane są manekiny testowe. Releguję do Uzupełnienia opis zrzucanych pionowo w eksperymentach sekcji kadłubów i niektórych doświadczeń z rozbijaniem całych samolotów. Wiedza uzyskana w tych badaniach pozwala ocenić, że przyspieszenia ciał ludzi są proporcjonalne do przyspieszeń na elementach konstrukcyjnych samolotu, a współczynnik proporcjonalności zależy od tego w którym kierunku fotel lotniczy jet przyspieszany, czy pozostaje zamocowany do podłogi, czy pasażer jest mocno przypięty pasem do fotela, czy odwrotnie - ma pas za bardzo poluzowany. A te rzeczy są inne w przypadku normalnego i odwróconego do góry kołami spadku samolotu na ziemię. Odwróconych upadków nigdy nie testowano. Dlatego liczby podane w Uzupełnieniu nie są wiarygodnym oszacowaniem wypadku smoleńskiego. Dochodziły one jednak typowo do wartości kilkudziesięciu g,  maksymalnie nawet większych (100g!), w doświadczeniach gdzie zrzucano sekcje kadłuba z wysokości zaledwie 2-3 m.

Ogólne cechy przenoszenia przyspieszeń z konstrukcyjnych elementów samolotu na podłogę kabiny, fotele i ciała pasażerów są podobne. Może dochodzić zarówno do zmniejszenia przeciążeń którym poddana jest podłoga kabiny pasażerskiej przy przenoszeniu ich na ciała pasażerów przez fotele i pasy (gdy fotele wyginają się w zaprojektowany, ograniczony sposób i pochłaniają energię uderzenia a pasy cały czas mocno trzymają), jak i do wzmocnienia przeciążeń konstrukcji, gdy mocowanie pasażera do struktury jest wadliwie zaprojektowane (np. zbyt elastyczne,  albo luźne pasy bezpieczeństwa) a konstrukcja jest zbyt sztywna lub odwrotnie - zbyt giętka. Ekstremalnie niebezpiecznym przypadkiem jest pasażer nie przypięty pasem, zerwanie pasa bezpieczeństwa,  lub fotela z podłogi, gdyż to praktycznie gwarantuje bardzo gwałtowne spotkanie z czymś twardym.

Pasażerowie w zderzeniach samochodowych

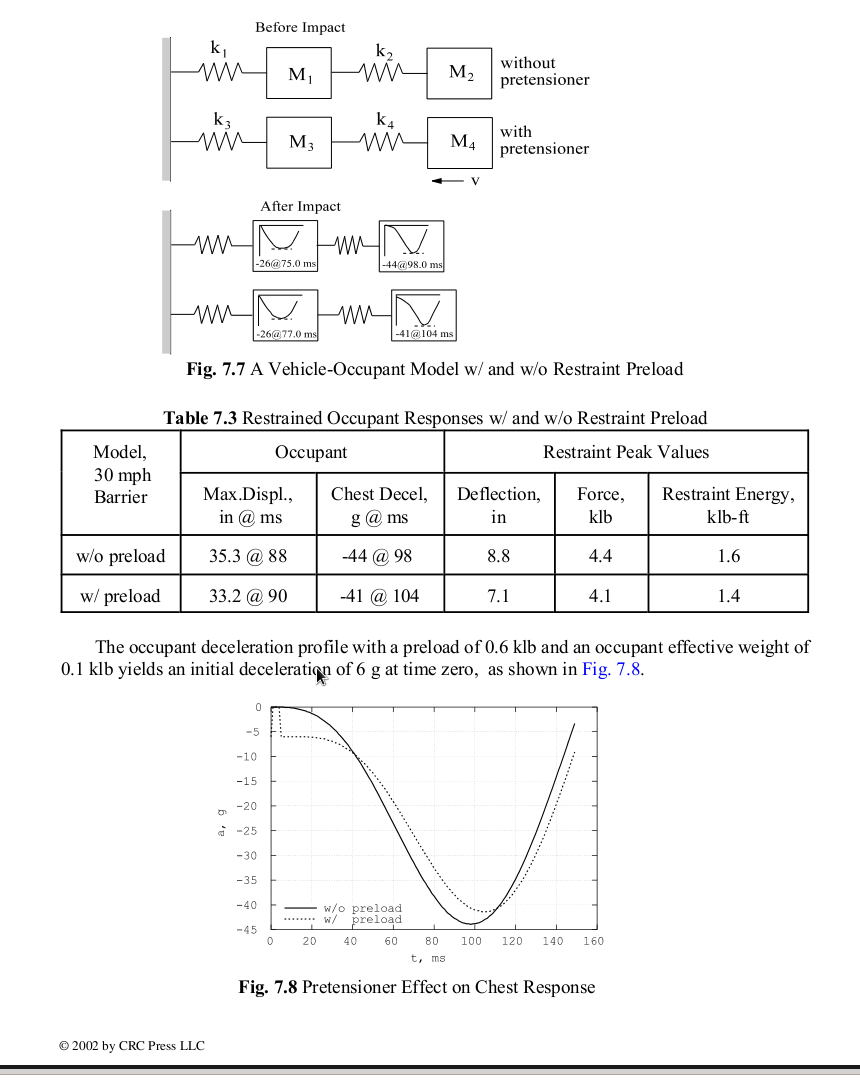
M. Huang w książce "Vehicle Crash Dynamics"  (CRC Press, 2002) opisuje modelowanie i realne testy zderzeń samochodowych. Można by spróbować obliczyć podobne modele obciążeń i przyspieszeń części ciała pasażera w wypadku smoleńskim, gdyby pasażerowie byli przypięci pasami, a fotele przyczepione do podłogi, deformowalne przeszkody w samolocie znane i realistycznie modelowane. Nie wchodzę w szczegóły modelowania wypadków samochodowych, jako że te warunki nie były spełnione. Dodatkowo, pas samochodowy składa się z dwóch pasów: biodrowego idącego na ukos przez klatkę piersiową. Oprócz tego pas ma obecnie tzw. pretensioner (urządzeni napinające), tj. w razie wypadku jest napinany, zmniejszając zabójczy dla człowieka luz i zmniejszając w pewnym stopniu odczuwane przyspieszenia. Mimo to, przyspieszenia przy modelowanym zderzeniu samochodu (plastycznie odkształcanego z realistyczną odległością zgniotu) w uderzeniu o twardą ścianę z prędkością  13.4 m/s (30 mph, 48 km/h), która jest zauważalnie MNIEJSZA niż 20 m/s,  składowa pionowa zderzenia smoleńskiego, są b. grożne dla życia, co ilustrują poniższe rysunki. Pierwszy pokazuje wyniki eksperymentalne (przyspieszenie klatki piersiowej pasażera i kierowcy), drugi obliczeniowe.

Awaryjny naciąg pasów powoduje początkowe przeciążenie 6g i zmniejsza maksymalne przeciążenie działające na klatkę piersiową przypiętego pasami samochodowymi pasażera z 44g do 41g. Obie wartości są bardzo groźne.




Fotele lotnicze i pasażerowie PLF 101

Samolot spadł w przechyle ok. 150 stopni z prędkością pionową 20 m/s. Poszycie górnej części kadłuba ('dachu') ma bardzo małą grubość ~2 mm i natychmiast odkształca się, nity są zrywane. Przy 70 m/s prędkości poziomej, obecności przeszkód naziemnych takich jak nierówność terenu, drzewa, poszycie  zostanie zerwane i zniszczone w ciągu nie więcej niż kilkudziesięciu milisekund. Pozostaje struktura nośna kadłuba: wręgi kołowe rozłożone co ok. 50 cm, oraz wzmocnienia (stringery) w postaci podłużnych profilowanych listew z cienkiej blachy (3-3.5 mm). Struktura ta jest wytrzymała na różnice ciśnienia i przeciążenia w normalnej eksploatacji samolotu. Nie może zatrzymać spadku ciężkiego samolotu.  Kadłub jest obliczony na siły radialne, ciśnieniowe, a nie na występujące w lesie smoleńskim główne naprężenia ścinające (masywniejszy spód samolotu nie ma kontaktu z ziemią i przez inercję wlecze za sobą hamujące cały samolot wręgi, powstaje naprężenie ścinania). Uderzenie masywnego samolotu wbija nieznacznie wręgi ze stringerami w szybko przesuwający się względem samolotu grunt, co bardzo szybko wybrzusza stringery oraz składa wręgi na płasko. Jedyne części dachu które mogą przetrwać pierwsze uderzenie to te, które chronił przez kontaktem z gruntem ogon, ale tylko bardzo krótko, bo ogon odłamał się zaraz po uderzeniu w ziemię, o czym opowiedzieli świadkowie wydarzenia, pracownicy i kontraktorzy na terenie serwisu samochodowego KIA w odległości 200 m od miejsca spadku PLF 101, o czym pisałem w rozdz. 71.

Zderzenie z ziemią generuje jak oceniliśmy to powyżej przyspieszenia podłogi co najmniej 25 g. Co dzieje się z fotelami lotniczymi? Odrywają się od podłogi. Fotele spełniają wymagania certyfikacji z zapasem bezpieczeństwa 1.33. Wypada więc zapytać o te wymagania. Polecam rozdziały 8 i 9 książki Georga Bibela "Beyond the Black Box. The forensics of airplane crashes" (JHU Press, 2008) zatytułowane, odpowiednio: Crash Testing, oraz Human Tolerances to G Loads and Crash Forces. Certyfikacja foteli lotniczych jest nastawiona na zapewnienie odpowiedniej sprężystości i plastyczności w uderzeniach samolotu w ziemię pod ostrym kątem, w pozycji mniej więcej horyzontalnej. Inercja pasażera działa wtedy głównie w dół i częściowo do przodu, podczas gdy w Smoleńsku zadziałała do góry i tylko częściowo do przodu.



Rysunek podaje wymagania certyfikacyjne w próbach statycznych z lat 80-tych.Odpowiadają one siłom wyrywającym 3-osobowy fotel w zaznaczonych kierunkach, dochodzącym do 2500 kG. Podłoga samolotu była projektowana na przenoszenie takich sił, lecz nie dużo większych (chodzi nie tylko o oszczędność wagową, ale o to by podłoga poddawała się plastycznej deformacji w zderzeniach które w przeciwnym przypadku byłyby śmiertelne. Od 1988 r. (formalny wymóg od 2005 r.), liczby podane na powyższym rysunku zmieniono na 3g w kierunku pionowym, 4g bocznym, w pozostałych kierunkach nie były zmienione (dodano tylko wymaganie 1.5g w kierunku przeciwnym do kierunku lotu). FAA dodała też wymaganie dwóch testów dynamicznych, jeden gdzie na pasażera działa 14 g w kierunku odchylonym do przodu o 30 stopni od pionowo (w dół) jak przy spadku na ziemię w normalnym, poziomym ułożeniu kadłuba, drugi zaś ma symulawać zderzenie z przeszkodą na ziemi (16 g poziomo). Standardy opisujące wyrywanie fotela w górę nie były zmienione.

Mnożąc przez margines bezpieczeństwa 1.33, widzimy że fotele wyrywane pionowo w górę odrywają się od podłogi przy przeciążeniu około 3*1.33 = 4g (można przyjąć nawet 3*1.5 = 4.5g; z drugiej strony, jeśli fotele TU-154M nie spełniały zachodnich wymogów, mogły oderwać się przy mniejszym przeciążeniu).

Wniosek jest oczywisty: przy odwróconym spadku na ziemię można oczekiwać oddzielenia się foteli pasażerów od podłogi po pierwszym uderzeniu samolotu w ziemię. Fotele zerwane zostały nie tylko pionowo w górę w stosunku do podłogi, ale też w bok, gdyż skrzydła samolotu w momencie spadku były nachylone 30^o  do horyzontu  (sin 30^o = 1/2).  Warunki katastrofy były znacznie gorsze niż standardy certyfikacyjne i doświadczalne zderzenia samolotów z przeszkodami prowadzone przez FAA/NASA, za wyjątkiem myśliwca wysłanego prosto na betonową ścianę.


  75.5.   KRYTERIA   PRZEŻYWALNOŚCI   KATASTROF  LOTNICZYCH

Jako pasażer samolotu spadającego na ziemię, masz niebagatelną szansę przeżycia, jeśli

1. Jesteś przypięty/przypięta pasem do fotela lotniczego, który nie oderwał się od listw mocujących, a te od podłogi, która nie porwała się uwalniając fotele. Historycznie, przykładem zasadniczej roli tego kryterium jest wypadek Kegworth Flight 092. W Smoleńsku, jak omówiliśmy to przed chwilą, to kryterium nie było spełnione.

2. Tzw. safe space. Nie zderzasz się z niczym, na przykład meblami czy szafkami pokładowymi, częściami samolotu. Nic ci nie obcina kończyn ani nie zgniata głowy. W przypadku sekcji samolotu przyspieszanych 16g, kiedy głowa manekina napotykała przedmioty, przeciążenie na nią działające sięgało od 100g do 140g. To też była przyczyna śmierci w Smoleńsku, w związku z oderwaniem foteli, a także u osób nie przypiętych pasami.

3. Przyspieszenie działające na części Twego ciała (trwające tyle ile ile zwykle trwają przy zderzeniach, tj. < 0.1s) są mniejsze niż krytyczne. W praktyce oznacza to mniej niż 50g. Jeśli samolot spada do góry nogami, w pierwszym uderzeniu o ziemię gdy  a = 25 g zwykle pękają kręgi szyjne C1-C2 i masz złamanie nosa i kontuzję płuc, przy 50 g zaczynają ci się łamać różne kości i doznaje uszkodzeń wewnętrznych aorta, przy 80-100 g aorta kompletnie się urywa. W pewnym teście w USA manekin poddany był a = 30g. Zerwał pas fotelowy, pofrunął w stronę sklejkowej bariery grubości 2.5 cm, przebił ją i zatrzymał się dopiero po przebyciu 200m. W rozdziale 9 wspomnianej już książki G. Bibela "Poza czarnymi skrzynkami. Badanie wypadków lotniczych" jest tabela 9.7, podająca najzwięźlej kryterium przeżywalności przy różnych głównych kierunkach działania przeciążenia. Ponieważ oczy są jednym z najczulszych organów, podaje się kierunek opisując w którą stronę chcą wypaść. W Smoleńsku mogły działać różne siły, najgorsze są boczne (eyeballs left/right, limit = 9g), jednak pierwsze uderzenie działało w górę na oczy (eyeballs up, limit = 15g).

Kryterium 3 oparte o przyspieszenia nie było spełnione, ponieważ oderwanie foteli od podłogi spowodowało zderzenia z małą drogą hamowania i w konsekwencji przyspieszenia organów znacznie większe, niż w idealnym przypadku gdy jesteśmy mocno przypasani do fotela i podłogi, a deformuje się plastycznie struktura samolotu pod podłogą.

Klasyfikacja wypadku 10.04.10 w ramach badań amerykańskiej agencji NTSB byłaby jednoznaczna i oczywista: unsurvivable. Nie powinno dziwić to, że na podstawie oględzin uszkodzeń organów wewnętrznych ofiar katastrofy, komisja MAK uznała, że ciała poddane były przyspieszeniom rzędu 100g. Z analizy fizycznej wynika, że jak najbardziej mogły być.


  75.6.   ZAKOŃCZENIE

Udowadnianie na podstawie wzoru na ruch jednostajnie opóźniony na drodze poziomej równej długości wrakowiska, że przyspieszenia były dwa rzędy wielkości mniejsze niż naprawdę, pozostawić należy ludziom karygodnie niewykształconym. Spadek PLF 101 z dużą prędkością pionową i przechyłem 150 stopni, w warunkach nie symulowanych nigdy przez FAA i NASA, poskutkował gwałtownymi przeciążeniami elementów strukturalnych kadłuba (rzędu 100g). To odebrało pasażerom szansę przeżycia. Już od naprężenia pasów bezpieczeństwa pasażerowie w momencie uderzenia w ziemię mogli otrzymać silne urazy. Groźniejsze było to, że fotele oderwały się od podłogi i wyrzucone zostały ze znaczną prędkością w kierunku niszczonych struktur kadłuba i gruntu. Wszystkie praktycznie ciała i części ciał były dlatego mocno ubłocone, a fotele połamane i oderwane od podłogi. Podejrzewam, że deformacja góry kadłuba w niektórych sektorach była tak duża, że bezpieczna objętość powietrza wokół wielu pasażerów spadła do zera, a hamowanie ciężkiego samolotu (zwłaszcza od strony uderzenia czyli lewej burty) odbywało się przez bezpośrednią styczność foteli i ludzi z ziemią. Wielu zmarłych doznało wielkich urazów głowy, gdyż ta część ciała była narażona najbardziej przy uderzeniu w danej pozycji kadłuba. W każdym razie, wnioski patomorfologów o przyspieszeniach rzędu 100g znajdują  potwierdzenie w analizie fizycznej.

Wspomnę mimochodem wątpliwą informację, jakoby 35 ciał miało zerwaną odzież. To nieuzasadniony wniosek J. Jabczyńskiego (blogera salonu24 "fotoamatora"?), członka tzw. podkomisji Macierewicza. Trzeba jednak przyznać, że skoro opisany wypadek urywał kończyny, częściowe zerwanie odzieży jest więcej niż możliwe. Informacja o pasażerze jakoby rozpędzonym hipotetycznym wybuchem w kierunku tylnej grodzi i "owiniętym w drzwi tylnej toalety" okazała się za to całkowitym kłamstwem, o czym niedawno doniósł na swoim blogu stanzag (St. Zagrodzki).

W wypadku smoleńskim wszyscy zginęli i było to w dniu katastrofy szokujące. Niektórzy do dziś nie mogą w to uwierzyć. Są tacy którzy wolą wierzyć cynicznemu manipulatorowi i fałszerzowi, 2-mu sekretarzowi generalnemu KC Partii, że w samolocie zainstalowane było do 9 różnych bomb (jak można policzyć w opracowaniach jego nielegalnej 'podkomisji'). W rzeczywistości zaś niewłaściwie szkoleni i nie kontrolowani okresowo przez pułk piloci złamali elementarne reguły bezpieczeństwa bardzo trudnego rodzaju podejścia, jakiego nigdy w składzie załogi, ba, nawet indywidualnie na tym typie samolotu, nie ćwiczyli. W momencie, gdy piloci wlatywali sprawnym samolotem TU-154M pod poziom pasa 26 lotniska Siewiernyj, los pasażerów był przesądzony. Choć uniknęli uderzenia w ziemię w rejonie bliższej radiolatarni NDB, nie było już możliwości uniknięcia zderzenia z 16-metrową, masywną brzozą, na której oderwała się dużą część lewego skrzydła, nie było też szansy utrzymania sterowności samolotu i uniknięcia obróconego upadku w las.

Katastrofa smoleńska nie była możliwa do przeżycia, wg wszystkich kryteriów, powszechnie stosowanych przez państwowe komisje badania wypadków lotniczych na całym świecie. Czy zdarza się, że ktoś przeżywa mimo takiego werdyktu? Tak, bo werdykt odnosi się do znacznej większości, ale niekoniecznie do wszystkich bez wyjątku pasażerów. Niestety takiego szczęścia nie miał żaden pasażer PLF 101. A jeśli lekarz mówi "pacjent nie przeżyje" i faktycznie tak jest, głupio debatować dlaczego się nie pomylił.


(c) P. Artymowicz,   9  lipca 2021


______________________________________________________________________________

UZUPEŁNIENIE:   PRZYSPIESZENIA  OBSERWOWANE  W  CRASH  TESTACH

W latach 70tych FAA i NASA wraz z Boeingiem, Lockheedem i McDouglasem, zdefiniowały zakres parametrów zderzeń samolotów z ziemią, które pasażer może przeżyć (survivable, "przeżywalne" czy możliwe do przeżycia) na podstawie 126 dobrze udokumentowanych wypadków. Częścią badań były tzw. CID = Controlled Impact Demonstrations, lub krócej: crash testy starych samolotów obłożonych miernikami. Leciały w nich lub spadały na ziemię w laboratorium podobnie wyposażone manekiny.

Najsłynniejszy chyba crash test na pustyni samolotu Boeing 720 w 1984e r. Mimo 14 wstępnych prób zdalnego pilotażu samolotu w kierunku pustynnego poligonu doświadczalnego, w eksperymencie zawiódł... pilot. Samolot nie spadł po planowanej trajektorii, w planowanym ułożeniu kadłuba względem pustyni, co jest spójne ze statystyką wypadków: przyczyną 4 na 5 wypadków lotniczych w Ameryce są piloci. Podobna była przyczyna w Smoleńsku. Test niezupełnie się udał pod pewnymi względami (w samolocie miało nie zapalić się paliwo ze specjalnymi dodatkami, niestety uzyskano spektakularną kulę ognia i pożar), ale były użyteczne dane o przeciążeniach. Samolot zaczepił lewym silnikiem o ziemię za wcześnie, co spowodowało jego obrót na nos (zmniejszenie pochylenia). Siły były większe w części przedniej kadłuba, która uderzyła w ziemię (w pozycji mało przechylonej) z prędkością Vz = 18 ft/s, czyli 3.6 raza wolniej niż spadał PLF 101, podczas gdy ogon uderzył tylko 6 ft/s (10 razy wolniej niż PLF101). Środek masy koło centropłatu spadał 12 ft/s, czyli 5.5 razy wolniej niż PLF 101. Co zarejestrowały akcelerometry? Największe obciążenie pionowe przy podłodze zarejestrowano w rejonie kokpitu (14 g), najmniejsze (3 g) w tylnej kabinie pasażerów. Przeciążenia poziome rozkładały się podobnie, lecz były niższe, do 7  g z przodu i 4 g w środku i z tyłu kadłuba. Przeciążenia boczne dochodziły do 5 g. To było oczywiście bardzo delikatne zderzenie w porównaniu ze smoleńskim, chodzi tu jednak nie o wartości a o skalowanie przeciążeń z prędkością. W tym przypadku, przeciążenie miało skalowanie
a ~ V_z^3/2 ,
takie jakby droga hamowania (deformacja struktury) wydłużała się wraz z pierwiastkiem kwadratowym z prędkości S ~ V_z^1/2  (przy spadku pionowym mierzony czynnik obciążenia równy jest  g + a = g + V_z²/2S).

Tam, gdzie struktura obręczy (wręg) kadłuba gięła się plastycznie, największe przeciążenia zapisały się na spodzie kadłuba, który uderzał w ziemię (a=32 g) i na poszyciu sufitowym (a=25 g), mniejsze na burtach (a=7-9g), podczas gdy zarówno podłoga w rożnych miejscach mocowania fotel, same fotele i biodra manekinów do nich przypiętych pasami wszystkie poddane były działaniu tych samych przeciążeń około 6 g (Hayduk, NASA Conf.Publ. 2395). Teoretycznie może dochodzić zarówno do zmniejszenia przeciążeń przy przenoszeniu ich na ciała pasażerów przez fotele i pasy (gdy fotele wyginają się w pewien ograniczony sposób i pochłaniają energię uderzenia a pasy cały czas mocno trzymają), jak i do wzmocnienia przeciążeń gdy mocowanie pasażera do struktury jest wadliwie zaprojektowane (np. zbyt elastyczne lub luźne pasy bezpieczeństwa). Jak widać, czasem te efekty się wzajemnie kasują i części ciał poddane są przyspieszeniom takim jak podłoga samolotu.

Tam, gdzie nie było plastycznego bufora, tj. nad sztywnym centropłatem, wysokie przyspieszenia struktury samolotu przenosiły się mało zmienione na podłogę, siedzenia i ciała ludzi : High loads were transmitted from the bottom of the fuselage to the floor and into the seats and crash test dummies. Maximum normal accelerations were 70 G at the fuselage bottom, 70 to 95 G at the cabin floor, and 40 to 60 G at the dummy pelvis.

Do 2/3 przeciążenia kadłuba było rejestrowane na częściach 'ciała' manekinów testowych.
Jest więc wiele rożnych możliwych mnożników przyspieszenia kadłuba, dających końcowe przyspieszenie którym poddane są części ciała. Ale ponieważ nie badano testowo nigdy spadku odwróconego jak w Smoleńsku, wyniki badań inżynieryjnych FAA/NASA nie przenoszą się dosłownie na wypadek smoleński, który był bardziej destruktywny.

W prowadzonym w ramach tego samego programu kontrolowanych zderzeń rodzaju badań zrzucano nieruchome początkowo sektory kadłuba wraz z manekinami na siedzeniach; to tzw. drop tests. Chodziło o wywołanie umiarkowanych przeciążeń dla testowania foteli i trwałości półek nad głowami, jednak mierzone przyspieszenia były często zaskakująco wysokie. Raport TM-85705 NASA mówi, że przy swobodnego spadku pokazanej poniżej sekcji samolotu z wysokości zaledwie 2 m dochodzi do groźnych przeciążeń struktury kadłuba, aż do 100g.

Zobacz galerię zdjęć: