73. Katastrofa smoleńska. Siła odrywająca skrzydło i jej działanie na brzozę

Wygodnym kluczem do zrozumienia jak lewe skrzydło samolotu rządowego nr. 101 rwało się na pniu brzozy lekarza Bodina, i dlaczego brzoza pękła w dwóch różnych miejscach i złożyła we dwoje, jest siła nacisku jednego ciała na drugie (i drugiego na pierwsze, zgodnie z 3. zasadą dynamiki). Policzona trzema różnymi metodami, siła rwania skrzydła wahała się wokół wartości rzędu 30-35 Ton (36 T i aż 40 T w rożnych oszacowaniach analitycznych). To wyniki prac amerykańskiej uczelni MIT i polskiej akademii WAT. I dokładnie taka wartość ~34 T skutkuje charakterystycznym złamaniem brzozy Bodina w moich symulacjach dynamicznych zderzenia! To potwierdza obserwacje kilku naocznych świadków, mówiące o odpadnięciu części skrzydła na brzozie i jej złamaniu przez samolot TU-154M, badania molekularne wiórów znalezionych w urwanym skrzydle, jak i dokładne rekonstrukcje trajektorii wg zapisów rejestratorów, na których PLF 101 uderza w brzozę skrzydłem. Zobaczymy też konceptualnie, skąd biorą się loki i zafalowania metalu w miejscu przerwania skrzydła.

DLACZEGO TO WAŻNE

Jeśli siła konieczna do przerwania skrzydła jest większa niż iloczyn wytrzymałości drewna na zgniatanie boczne (dokładniej, suma wytrzymałości statycznej i efektu naprężenia dynamicznego zależnego od prędkości zderzenia, zob. rozdz. 50, suma ta to ~14 MPa) i największego możliwego pola styku brzozy i skrzydła, wówczas cały sektor pnia musi zostać zniszczony w zderzeniu. Oszacujmy: pole zgniatanego pnia to mniej więcej grubość skrzydła (~40 cm) razy średnica pnia (też tego rzędu), czyli miażdżenie całego uderzonego sektora brzozy wymaga olbrzymiej siły rzędu (0.40*0.46m² * 14 MPa = 2.6 MN ~ 260 T). To nie zaszło, gdyż jak pokażę, już siła o rząd wielkości mniejsza urywa skrzydło. Siła oddziaływania narasta w czasie uderzenia do wartości, powyżej której skrzydło jest stopniowo niszczone, po czym się mniej więcej stabilizuje. Zaś uszkodzenia pnia zatrzymują się w momencie, gdy pole kontaktu przyrasta do wartości takiej wartości, że naprężenia miażdżące włókna drewna spadają poniżej wytrzymałości drewna. Od tego momentu pień jest popychany, lecz nie wgniatany przez rwane skrzydło. Rzeczywiście, rekonstrukcja pnia brzozy Bodina przez polskich biegłych prokuratury w r. 2012 w Moskwie świadczy o tym, że brzozie brak mniej niż 10% materiału w sektorze zderzenia, poza tym górna i dół pnia pasują do siebie jak ulał. Część brakującego materiału brzozy znaleziono w skrzydle. Wykluczyło to hipotezę ścięcia brzozy.

Zatem skrzydło nie było wcale niezłomne, jak niefizycznie fantazjował wiele lat w oparciu o swe całkowicie błędne obliczenia dr Binienda z uniwersytetu w Akron, Ohio, a za nim wiele innych osób. Można wyznaczyć całkowitą siłę na styku ciętego skrzydła i pnia brzozy (nie na jeden element taki jak półka dźwigara, ale na wszystkie elementy) i pokazać następnie co dzieje się pod jej wpływem z brzozą wielkości brzozy Bodina. Podam cztery niezależne sposoby ustalenia siły, z których trzy są dobrze zgodne, a czwarty daje o 1/6 większe oszacowanie.

JAK WAT NAUCZAŁ BINIENDĘ

"Problemy modelowania numerycznego zagadnienia zderzeń ciał" (2013)
Andrzej Morka, Tadeusz Niezgoda, Paweł Dziewulski, Sebastian Stanisławek (WAT)

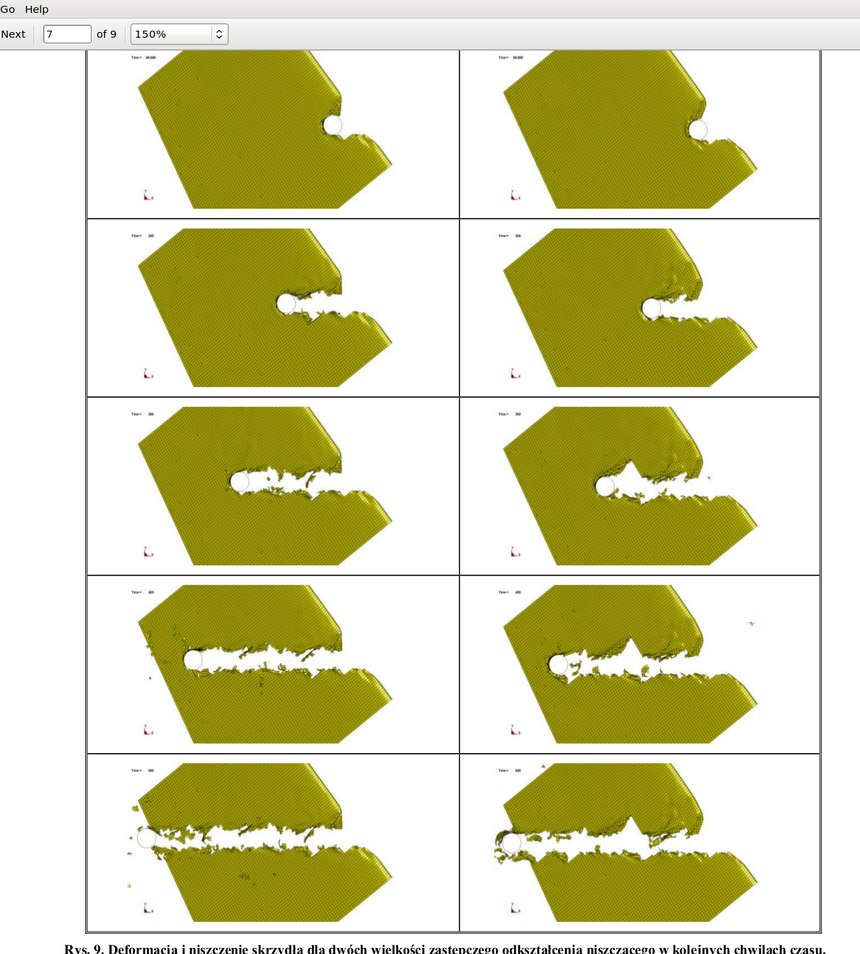
Reagując na szokujące błędy w pracach Biniendy w Wojskowej Akademii Technicznej przeprowadzono w grupie prof. Niezgody obliczenia przy użyciu tego samego narzędzia obliczeniowego (LS-Dyna), jednak z poprawnymi ustawieniami parametrów materiałowych i obliczeniowych. Wyniki prezentowane były później na tzw. 2giej konferencji smoleńskiej przez głównego autora prac, dr. Andrzeja Morkę. Nie znano, lecz rozsądnie szacowano możliwe grubości blach w skrzydle TU-154. Niedokładnie założono równej grubości blachy w elementach konstrukcyjnych. Wszystkie elementy: żebra, dźwigary I-III, listwy (stringery), poszycie, są bardzo cienkie, ale mają różną grubość, równą odpowiednio: 0.97 mm, 3.0-2.5-2.5 mm, do 3.5 mm, 2.5 mm (por. załączone w galerii rysunki). Również założono niedeformowalny cylindryczny pień, co nie zostało wtedy uzasadnione (dopiero model dynamiki łamania brzozy omówiony przeze mnie rok później uzasadnił poprawność tego założenia). Uwzględniono natomiast poprawne wymiary kesonu skrzydła i ułożenie wszystkich elementów, sprawdzono też wpływ otworów zmniejszających masę żeber (okazał się bardzo niewielki).

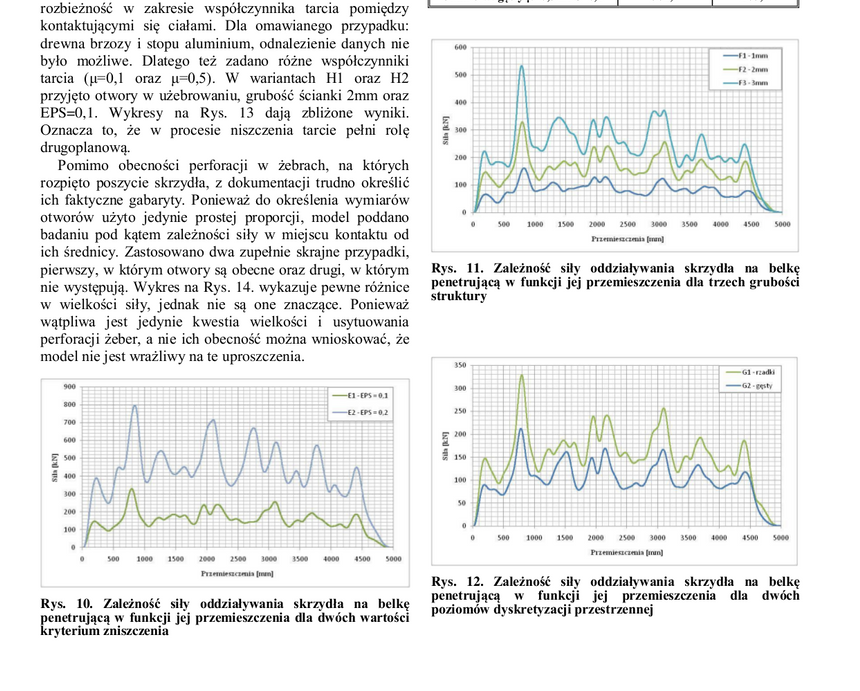
Siła w modelach najlepiej pasujących do rzeczywistych grubości blachy D16 w skrzydle tupolewa była zmienna w czasie, oscylowała w granicach 25-40 T w czasie cięcia (oczywiście miała maksimum odpowiadające destrukcji dźwigara I), i zależała nieco od rozdzielczości, ale głównie od parametru EPS_max skrzydła, kontrolującego erozję numeryczną elementów obliczeniowych (jest to numeryczna deformacja graniczna elementów FEM). Realistycznie, średnia siła generowana przy cięciu/rwaniu skrzydła przez przeszkodę równa była około 30-33 T (tak jak na rys. 10, jeśli w myśli interpolować wykresy do EPS_max = 0.15, co dobrze odpowiada granicznej deformacji stopu D16.)

W tzw. konferencjach smoleńskich brał udział dr Jan Błaszczyk z WAT, który wyznaczył analitycznie w pracy "Brzoza smoleńska - aspekty wytrzymałościowe struktury skrzydła TU-154" siłę rwącą skrzydło na F = 40 T rozpatrując schemat przekroju poprzecznego skrzydła i projektowane w konstrukcjach lotniczych naprężenia. Błaszczyk był autorem podręcznika konstrukcji samolotów wydanego przez WAT. Niewłaściwie doszedł do wniosku, że brzoza została ścięta pomiędzy zerwaniem dźwigarów I i II, lecz łatwo zrozumieć jak to się stało. Przy faktycznej wytrzymałości poprzecznej włókien brzozy równej 10.8 MPa (np. zob. tabelę w pracy Morki i w mojej cytowanej poniżej), której jego analiza nie objęła (rozpatrywał 2-6 MPa), wymagana do ścięcia brzozy o śr. 46 cm siła wyszłaby za ramki jego rysunku nr. 21 i równałaby się wg jego oszacowań ~130 T. Czyli dokładniejsze studium wytrzymałości drewna brzozowego zmieniłoby konkluzję. Poza tym, dopiero później Wojskowa Prokuratura Okręgowa w Wwie opublikowała szkicowo wyniki składania i analizy brzozy niezgodne z poglądem o ścięciu brzozy i dokończeniu łamania skrzydła przez moment siły nośnej (błędny, lecz popularny wsród polskich inżynierów lotn. w tamtym czasie pogląd).

PRACE TOMASZA WIERZBICKIEGO (MIT): NIEWYBUCHOWE ZAWIJANIE METALU, SIŁA CIĘCIA, MODY NISZCZENIA BLACHY

"Petalling of plates under explosive and impact loading"
Tomasz Wierzbicki
[Impact and Crashworthiness Laboratory, Dept. of Ocean Engineering, Massachusetts Institute of Technology]. International Journal of Impact Engineering 22 (1999) p. 935-954

W latach 90tych w Laboratorium Zderzeń MIT prowadził pracę nad katastrofami w żegludze dyrektor laboratorium prof. Tomasz Wierzbicki. Jego prace pokazują m.in. proces tworzenia płatków metalu przy rwaniu bądź to przez obiekty penetrujący blachy metalowe, bądź to w wyniku wybuchu, proces ten po ang. nazywa się petalling albo curling (tworzenie płatków/loków metalu). Jest naturalną konsekwencją plastyczności metalu powyżej naprężenia krytycznego i tworzenia się tzw. kolanka plastycznego w miejscu nacisku klina lub innej przeszkody na blachę.

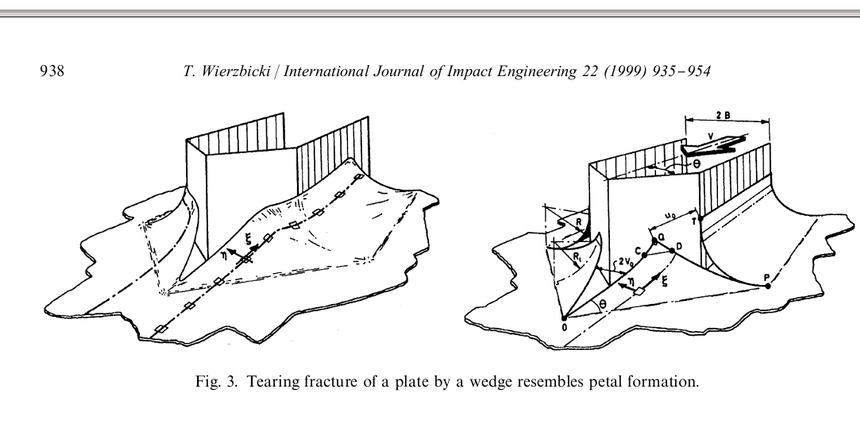
Taka jest teoretycznie policzona sekwencja powstawania loków:

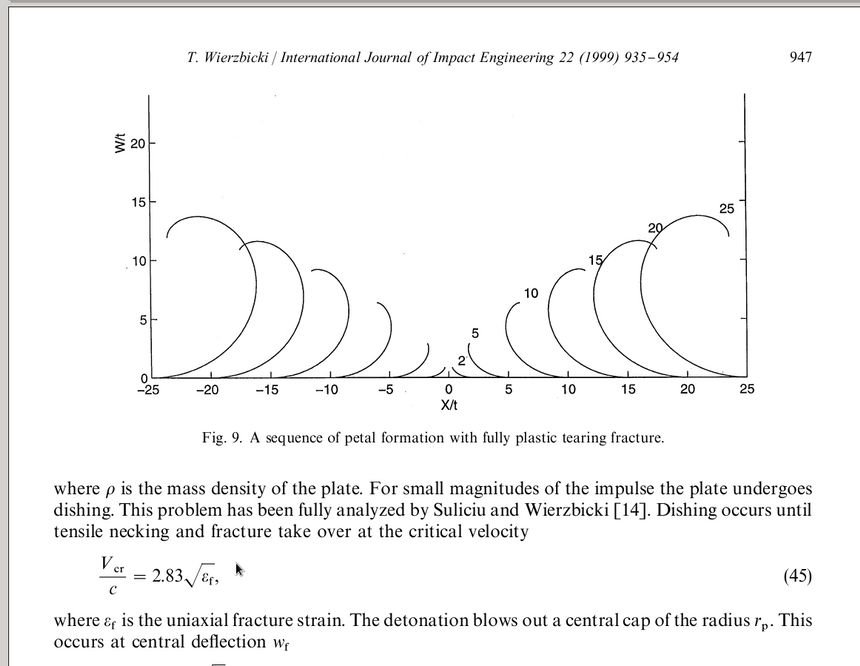
W pracy "Plasticity, fracture and friction in steady-state plate cutting" B. Simonsen i T. Wierzbicki (Int. J. Impact Eng. Vol 19, p. 667-691, 1997) omówili poprzednie modele kilku modów destrukcji płyt metalowych. Na przykład, obłe przedmioty takie jak pień mogą powodować rwanie ze zwijaniem poszycia w harmonijkę (concertina tearing = rwanie z fałdowaniem). Ostre kliny tną metal i zwijają go w płatki (loki) w sposób równowagowy, ciągły. Mogą też powstawać brzegi wyginające się na przemian w górę i w dół.Proces cięcia metalu jest dość skomplikowany, zawiera w sobie bowiem ciągłą propagację pęknięć przed przeszkodą, jak i zwijanie loków odginanych przez przeszkodę. Podano wzory teoretyczne na siłę i zestawienie z kilkoma pomiarami.

Podstawiając wartości odpowiadające zarówno właściwościom stopu TU-154 (limit plastyczny naprężenia 345 MPa) jak i kształtu najlepiej przybliżającego pień (kąt klina 90 stopni, szerokość 40 cm), oraz biorąc pod uwagę dwie warstwy poszycia (górne i dolne), otrzymałem oszacowanie siły tnącej F(x). Grubości fałdowanego poszycia są znane, ale nie wiadomo dokładnie jak traktować cięcie ustawionych pod kątem do kierunku cięcia innych elementów. Zakładam, że cieniutkie żebra i grubsze dźwigary jak i stringery są rwane tak, że uśrednione po czasie siły odpowiadają ciągłemu, wielomodalnemu cięciu blachy (z pękaniem i zwijaniem, blachy w loki, zob. równanie 65 cytowanej pracy) o zastępczej grubości x milimetrów. Oczywiste wydaje mi się, że należy wziąć grubość ~2.5 mm, ale możemy się posprzeczać. Po zrobieniu wykresu, w zależności od grubości x siłę całkowitą cięcia skrzydła przybliżyć można jako F(x) = 24T + 8T (x-1), gdzie x = 1...3 jest grubością ekwiwalentną blachy w mm. W ten sposób otrzymujemy dla x~2.5 wynik rzędu (średnia siła)

F(2.5) ~ 36 T (36 ton siły).

Ta siła zgadza się b. dobrze z wartościami obliczonymi później metodą numeryczną przez Morkę i in. (2013), jak też z dokładnością 1/6 z obliczeniami Błaszczyka.

PRACE PAWŁA ARTYMOWICZA (UofT): CO STAŁO SIĘ Z BRZOZĄ BODINA?

W roku 2014 przedstawiłem na konferencji Mechanics in Aviation XVI w Kazimierzu nad Wisłą swoje obliczenia , komplementarne w stosunku do obliczeń zespołu A. Morki. Modelując zachowanie całkowitej siły oddziaływania skrzydło-brzoza w funkcji długości cięcia skrzydła wg ich pracy, przyjąłem zakres średniej siły od 22 T do ponad 31 T. Uogólniłem teorię krótkiej belki cylindrycznej Timoszenki, w której uwzględnione są naprężenia ścinające i rotacja elementów belki, do przypadku zmiennego przekroju belki, oraz niezerowego obciążenia osiowego i możliwości rozchodzenia się oscylacji osiowych belki (tj. zmiany położenia wzdłuż kierunku belki). W ten sposób można uwzględniać efekty ciężaru ustawionej pionowo belki i ważną dla modelowania katastrofy smoleńskiej zmienną wraz z wysokością średnicę jej pnia. Najważniejsze pytanie brzmiało: jaka wartość siły przyłożonej na czas zderzenia do pnia (w sektorze zderzenia na wysokości 6.5 m nad ziemią) odtwarza znaleziony po katastrofie podwójny przełom brzozy: całkowity drzazgowy przełom w połowie pnia i częściowe pęknięcie pnia u podstawy. Odpowiedź brzmiała ok. 27 T.

Przedstawię teraz uaktualniony nieco model dynamiki łamania brzozy, używający dokładniejszych długości i średnic pnia, niż w oryginalnych obliczeniach. Uwzględnię średnicę u podstawy znaną teraz jako 74 cm i długość pnia 16 m (była mniejsza w poprzednich obliczeniach). Przez dodatkowe obciążenie masowe pnia na wysokości od 2 to 8 metrów uwzględniam fakt, że konary były tam zaczepione do pnia i stanowiły oczywisty balast w jego ruchu. Matematycznie, robię to przez przemnożenie gęstości pnia równej 9500 kg/m³ przez bezwymiarową funkcję m(z) = 1 + sin²(h)/4, gdzie h zmienia się liniowo od 0 do π pomiędzy h = 2m i h = 10m. Przyjmuję, że moduł łamania (modulus of rupture) równy jest MOR = 45 MPa, co jest niewygórowaną wytrzymałością, zgodną z wieloma źródłami nt. parametrów rosyjskiej brzozy. Dla większego realizmu symulacji, siła jest w obliczeniach zmienna w czasie wokół średniej wartości, w takim mniej więcej zakresie jak w obliczeniach LS-Dyna; na przykład tak jak tutaj

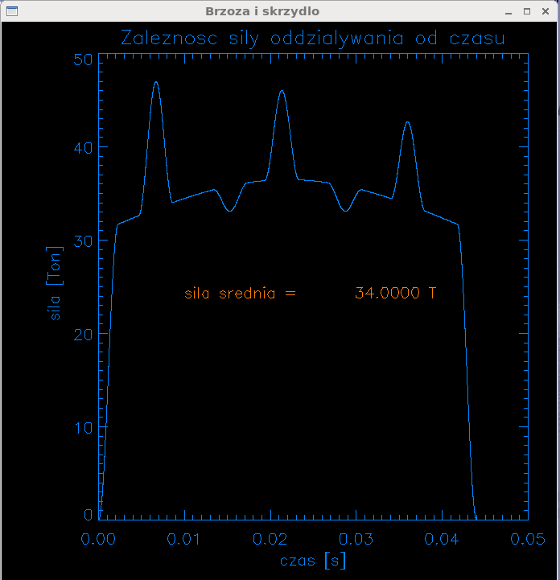
Uderzenie nie łamiące brzozy

Co stało się z brzozą, gdy napierała na skrzydło z siłą > 30 T? Oto krótka sekwencja maksymalnego uderzeniowego wyginania (bez łamania) brzozy Bodina przy średniej modelowanej sile 32 T.

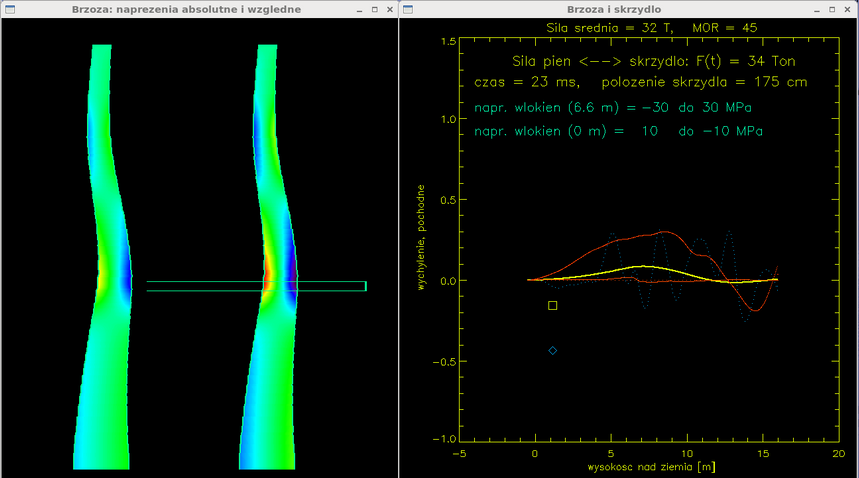
Czas = 23 ms. Na lewym panelu widać małe wygięcie pnia. Dla lepszej widzialności wygięcia, skala pozioma nierówna jest skali pionowej lewego rysunku. Żółta krzywa na prawym wykresie podaje wychylenie w funkcji wysokości w metrach. Poziomy pasek przesuwający się w prawo w miarę upływu czasu oznacza położenie ciętego skrzydła. Około 165 cm cięciwy skrzydła (ok 40%) jest w tym momencie przerwane. Dwie mapy kolorów podają naprężenia wewnętrzne w pniu. Kolor niebieski opisuje rozciąganie, czerwony ściskanie. Wartości maksymalnego naprężenia na dwóch interesujących wysokościach podane są liczbowo na prawym panelu (np. +30 MPa oznacza kompresję, -30 MPa rozciąganie skrajnych włókien).

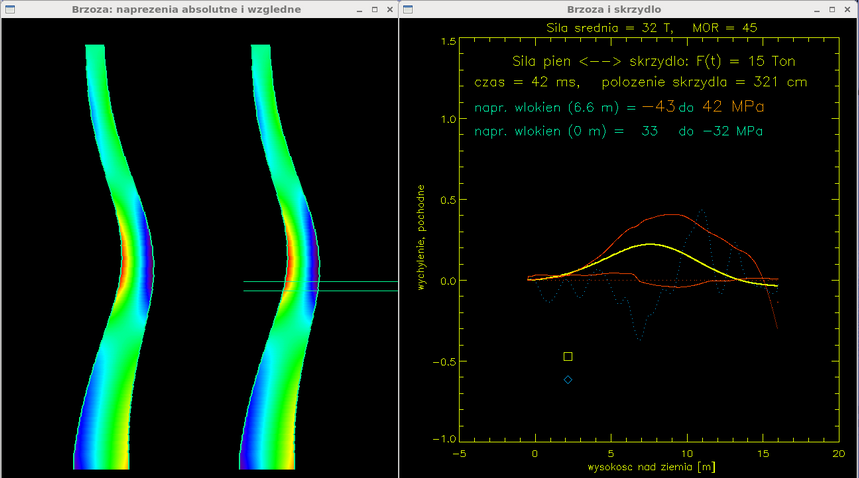
Czas = 42 ms. Wygięcie pnia, naprężenia rosną. Skrzydło jest już w zasadzie przecięte (jego położenie to 321 cm na prawo od początkowego), mimo to naprężenie rozciągające nie sięga wartości MOR = 45 MPa.

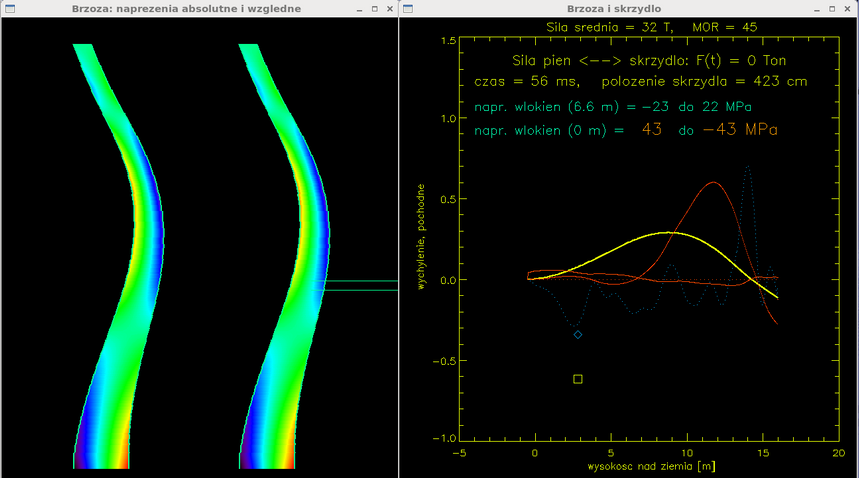
Czas = 56 ms. Wygięcie pnia powoduje maksymalne naprężenia u podstawy, nie prowadzą jednak do przerwania włókien. Skrzydło jest już całkowicie przecięte.

Uderzenie destruktywne dla brzozy

A teraz pokaże migawki z symulacji która łamie brzozę Bodina. W ramach modelu uogólnionej belki Timoszenki nie zajmuję się tu tworzeniem długich realistycznych drzazg ani historią powolnego upadku korony drzewa tak, że oparła się o pochylony dolny pień. Do tego potrzebne są modele o większej wymiarowości. Prowadzę obliczenia elastycznej brzozy do momentu początku jej łamania.

Czas = 14 ms. Tak jak w poprzedniej sekwencji obrazów, na lewym panelu widzimy wygięcie pnia pokolorowane na dwa sposoby. Żółta krzywa na prawym wykresie podaje wychylenie pnia w funkcji wysokości w metrach. Poziomy pasek przesuwający się w prawo symbolizuje położenie ciętego skrzydła ( w tym czasie przecięty jest już pierwszy dźwigar).

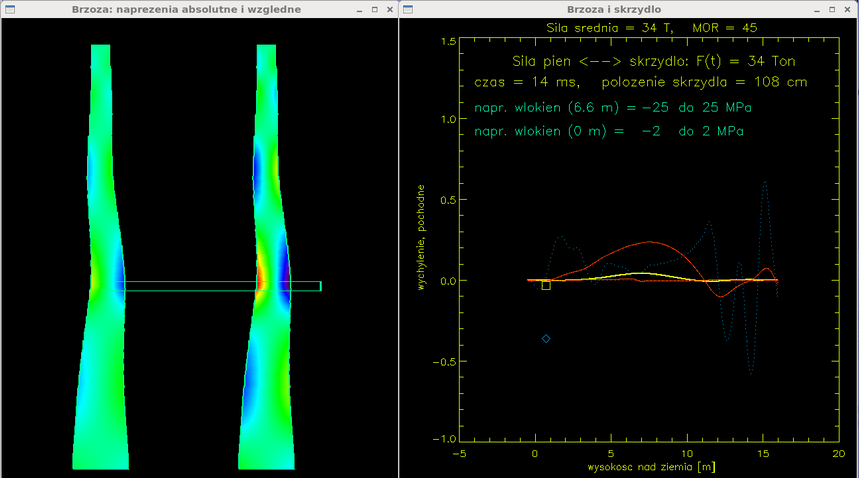
Czas = 36 ms. Wygięcie pnia i naprężenia rosną do poziomu bliskiego zerwaniu włókien (MOR = 45 MPa). Skrzydło jest w większości przecięte (jego położenie to 2.75m na prawo od momentu pierwszego kontaktu, ok. 2.5 cięciwy przerwane).

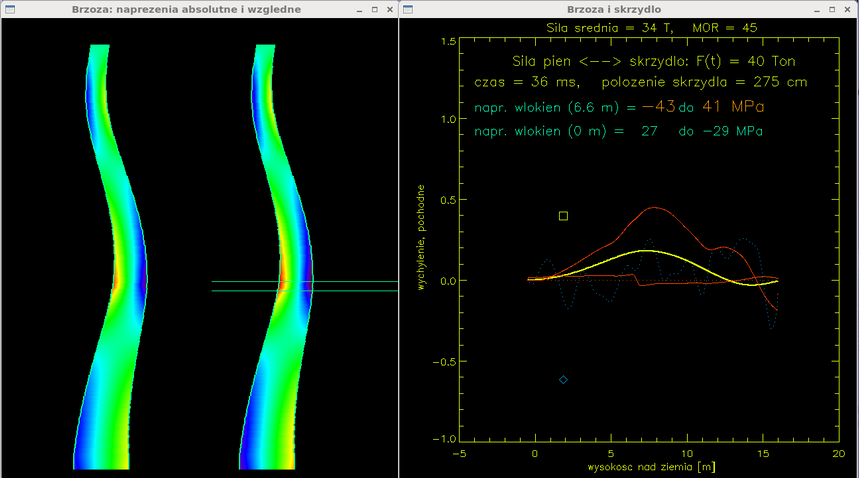
Czas = 43 ms. Gdy największe wygięcie pnia osiągnęło ok. 30 cm, naprężenia rozciągające przekroczyły wartość absolutną MOR = 45 MPa. Skrzydło jest w większości przecięte (jego położenie to 2.75m na prawo od momentu pierwszego kontaktu, ok. 2.5m z 3.5m cięciwy jest przerwane). Brzoza pękła w dwóch miejscach, na wysokości 6.5m i u podstawy. Przerwanie włókien jest graficznie zaznaczone jakby nastąpiło na całej szerokości pnia, co nie jest oczywiście prawdą (w rzeczywistości, na wys. 6.5m zaczął się w tym czasie tworzyć przełom drzazgowy, a u podstawy częściowe przerwanie włókien od strony wschodniej). To że przełom u dołu był częściowy a nie całkowity mówi mi, że średnia siła rwania skrzydła nie była znacznie większa niż minimalna potrzebna do przerwania włókien (34 T, w tym modelu).

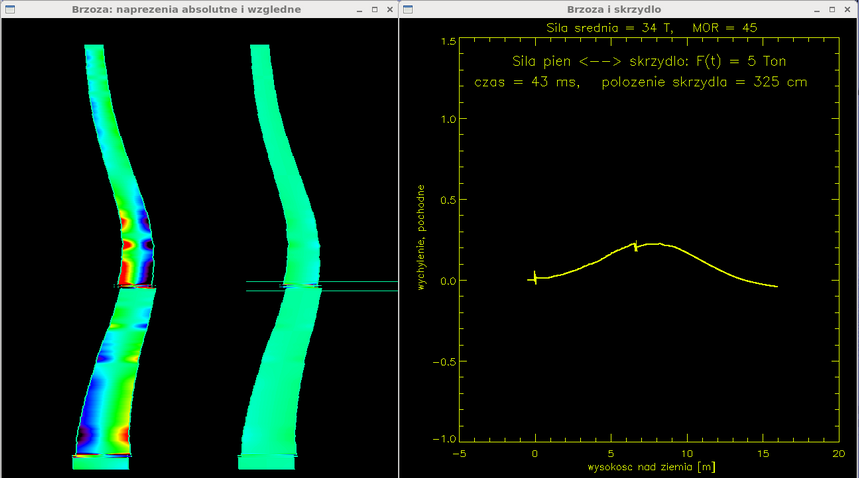
PODSUMOWANIE

Wygodną wielkością opisującą oddziaływanie brzozy na skrzydło i odwrotnie jest średnia siła nacisku całkowitego. Analityczna teoria Wierzbickiego, jak i numeryczne badania Morki przy poprawnym (w odróżnieniu od Biniendy) użyciu LS-Dyna, pozwalają oszacować tę siłę na 30-36 T (ton). Siła ta towarzyszy cięciu skrzydła TU-154M w rejonie, którym uderzyło w brzozę. Po uaktualnieniu mojego modelu, otrzymałem w wyniku zgodność mojej symulacji używającej siły średniej 33-36 T z tym co komisje, prokuratury i badacze niezależni znaleźli w Smoleńsku. Ciągłość włókien modelowanych przy użyciu wartości modułu łamania MOR = 45 MPa przerwana została marginalnie na wysokości uderzenia, jak i u podstawy brzozy Bodina, co doskonale tłumaczy to co się z brzozą faktycznie stało.

W brzozie znaleziono zielonkawe po jednej stronie blachy duralu D16 skrzydła, zaś w urwanym skrzydle, które przeleciało autorotując 110 m i spadło łagodnie (V ~ 20 m/s) w zarośla (co wiemy z mojego modelowania), znaleziono wióry brzozy. Po wykonaniu badań molekularno-biologicznych, laboratorium ministerstwa leśnictwa RF stwierdziło, że są to wióry z konkretnie tej brzozy tj. brzozy na działce lekarza pogotowia N. Bodina (drzewa tak jak ludzi można bowiem jednoznacznie rozpoznać na podstawie DNA).

Wszystko co opisałem stanowi ostateczny i niepowtarzalny dowód, że lot samolot PLF101 przed wypadkiem zniżył się niemal do poziomu gruntu, uderzył 10.04.10 w brzozę na wysokości 6.5 m i stracił tam 1/3 rozpiętości lewego skrzydła. To jak wiemy spowodowało, że stał się niesterowny i wszedł w niemożliwy do skontrowania lewy obrót w beczce typu lotkowego (tj. wywołanej momentem siły przechyłu, lecz nie wynikającej z przeciągnięcia i autorotacji) [por. rozdz. 23, 24, 28, 30, 32, 34].